 >仰望星空的人,不应该被嘲笑 ## 题目描述 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。 说明:不允许修改给定的链表。 进阶: 你是否可以不用额外空间解决此题? 示例 1:  ```javascript 输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。 ``` 示例 2:  ```javascript 输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。 ``` 示例 3:  ```javascript 输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。 ``` 提示: - 链表中节点的数目范围在范围 `[0, 104]` 内 - `-10^5 <= Node.val <= 10^5` - pos 的值为 -1 或者链表中的一个有效索引 来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/linked-list-cycle-ii 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。 ## 解题思路 两个快慢指针,从头节点出发,如果链表有环,快指针肯定可以在环内和慢指针相遇。没有环就不可能再相遇,相遇必在环内。 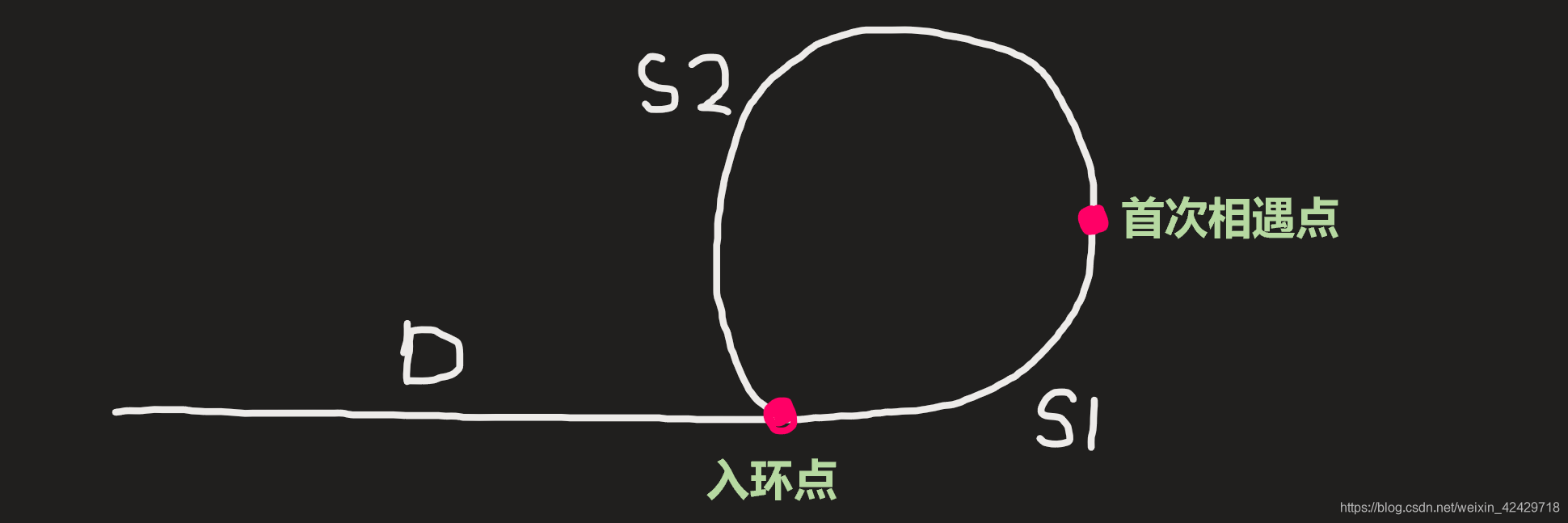 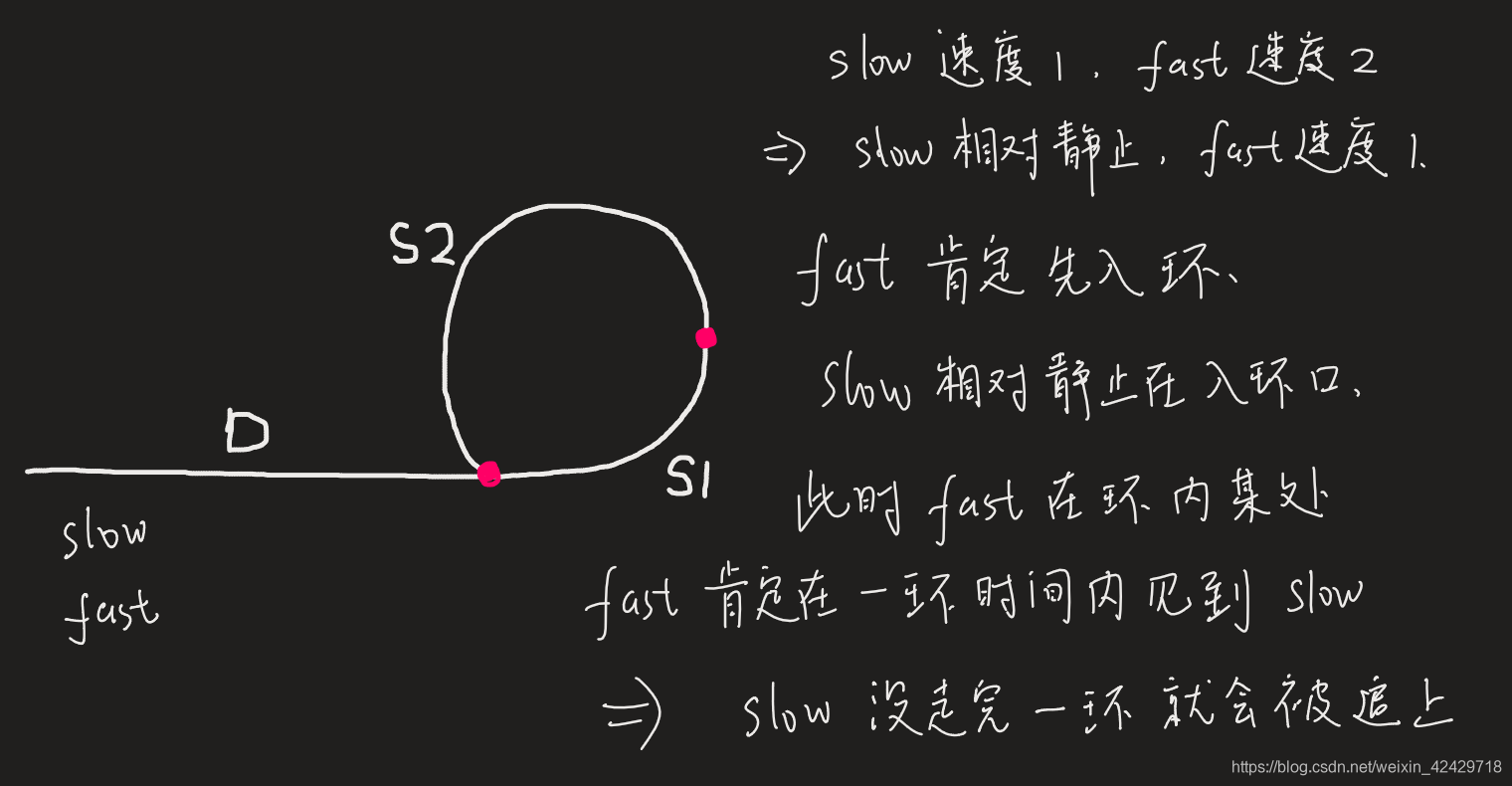 相遇时,慢指针走的距离:`D+S1D+S1` 假设相遇时快指针已经绕环 n 次,它走的距离:`D+n(S1+S2)+S1D+n(S1+S2)+S1` 因为快指针的速度是 2 倍,所以相同时间走的距离也是 2 倍: D+n(S1+S2)+S1 = 2(D+S1) 求解得到:**(n-1)S1+ nS2=D** 我们不关心在相遇时快指针已经绕了几次环,我们取 n = 1 ,消掉了 S1: **D=S2** 那么,当快慢指针第一次相遇时,将快指针放回到头节点,由于 `D=s2`,那么我们快慢指针一起走,都走1步,它们必定会走到入环点,然后相遇,此时就可返回对应指针下标。 ```javascript /** * Definition for singly-linked list. * function ListNode(val) { * this.val = val; * this.next = null; * } */ /** * @param {ListNode} head * @return {ListNode} */ var detectCycle = function(head) { let fast = head, low = head; // 首先,都从头节点出现 while(fast){ // 确保存在环 if(fast.next == null) return null; // fast.next 为null表示无环 low = low.next; // 慢指针走一步 fast = fast.next.next; // 快指针走两步 if(low == fast){ // 初次相遇 fast = head; // 快指针回到头节点 while(true){ if(fast == low){ return low; } fast = fast.next; // 快慢指针一起走 low = low.next; } } } return null; }; ``` 参考 <a href="https://leetcode-cn.com/problems/linked-list-cycle-ii/solution/141ti-de-kuo-zhan-ru-guo-lian-biao-you-huan-ru-he-/">笨猪爆破组</a> 图解 ## 最后 文章产出不易,还望各位小伙伴们支持一波! 往期精选: <a href="https://github.com/Chocolate1999/Front-end-learning-to-organize-notes">小狮子前端の笔记仓库</a> <a href="https://github.com/Chocolate1999/leetcode-javascript">leetcode-javascript:LeetCode 力扣的 JavaScript 解题仓库,前端刷题路线(思维导图)</a> 小伙伴们可以在Issues中提交自己的解题代码,🤝 欢迎Contributing,可打卡刷题,Give a ⭐️ if this project helped you! <a href="https://yangchaoyi.vip/">访问超逸の博客</a>,方便小伙伴阅读玩耍~  ```javascript 学如逆水行舟,不进则退 ```