|
26 | 26 |
|
27 | 27 | 我们都知道栈的特性是先进后出,我们借助栈来帮助我们完成前序遍历的时候。 |
28 | 28 |
|
29 | | -则需要注意的一点是,我们应该先将右子节点入栈,再将左子节点入栈。 |
| 29 | +则需要注意的一点是,我们应该`先将右子节点入栈,再将左子节点入栈`。 |
30 | 30 |
|
31 | 31 | 这样出栈时,则会先出左节点,再出右子节点,则能够完成树的前序遍历。 |
32 | 32 |
|
33 | 33 | 见下图。 |
34 | 34 |
|
35 | 35 | 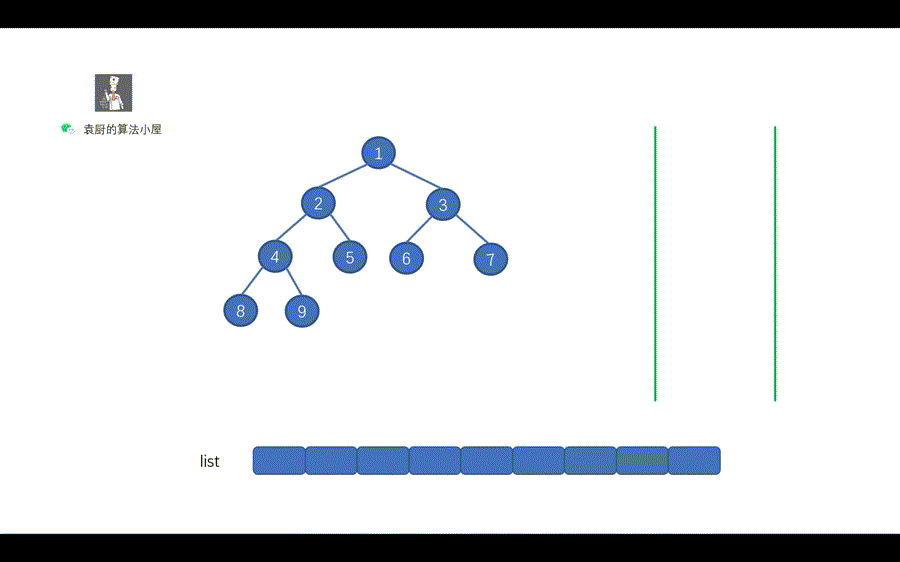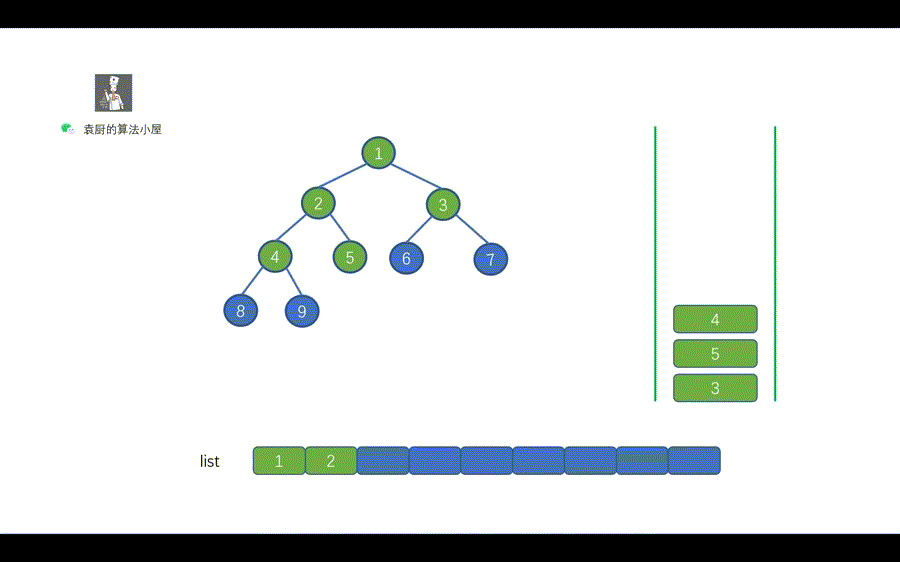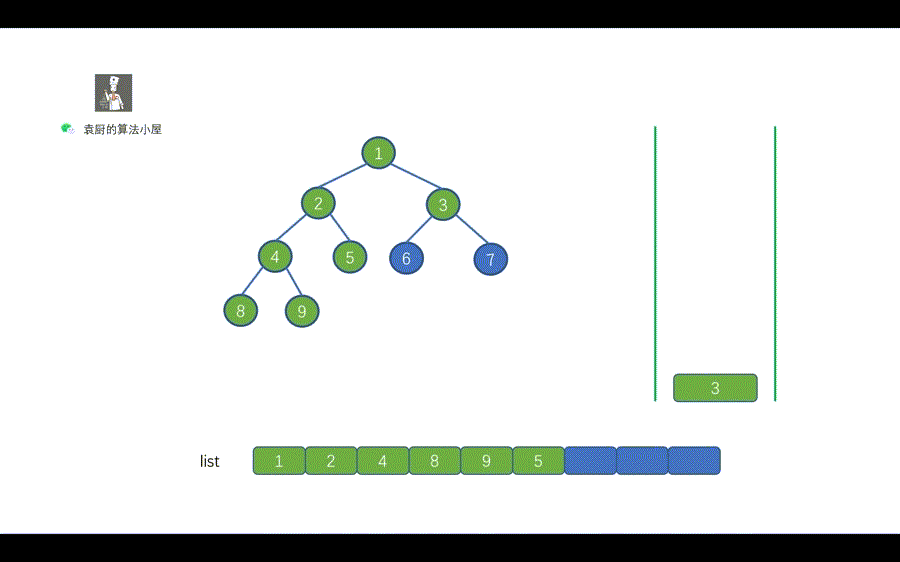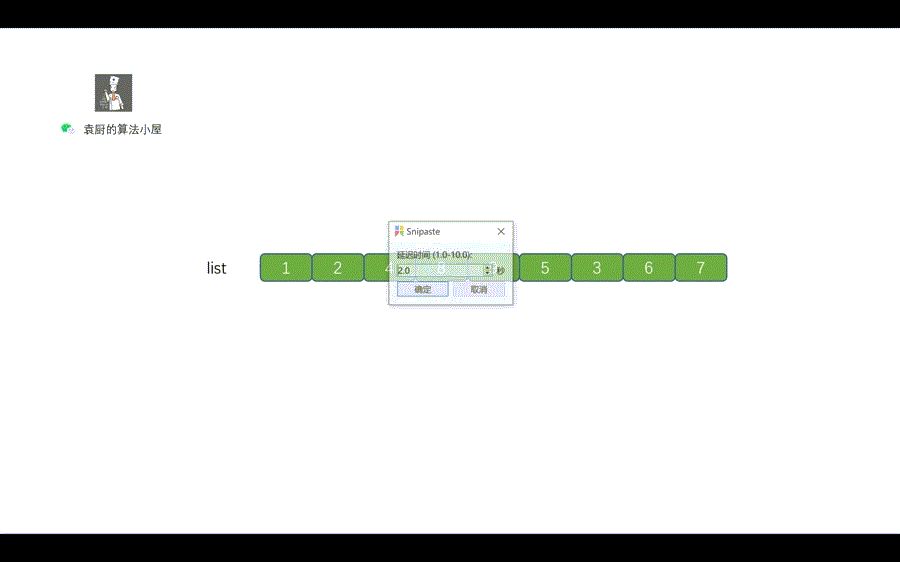 |
36 | 36 |
|
37 | | -我们用一句话对上图进行总结,当栈不为空时,栈顶元素出栈,如果其右孩子不为空,则右孩子入栈,其左孩子不为空,则左孩子入栈。还有一点需要注意的是,我们和层序遍历一样,需要先将 root 节点进行入栈,然后再执行 while 循环。 |
| 37 | +我们用一句话对上图进行总结,`当栈不为空时,栈顶元素出栈,如果其右孩子不为空,则右孩子入栈,其左孩子不为空,则左孩子入栈`。还有一点需要注意的是,我们和层序遍历一样,需要先将 root 节点进行入栈,然后再执行 while 循环。 |
38 | 38 |
|
39 | 39 | 看到这里你已经能够自己编写出代码了,不信你去试试。 |
40 | 40 |
|
@@ -69,7 +69,105 @@ class Solution { |
69 | 69 |
|
70 | 70 | ### Morris |
71 | 71 |
|
72 | | -Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空间开销的极限缩减。这个遍历方法,稍微难理解一些,不过结合动图,也就一目了然啦,各位系好安全带,我们要发车啦。 |
| 72 | +Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空间开销的极限缩减。这个遍历方法,稍微有那么一丢丢难理解,不过结合动图,也就一目了然啦,下面我们先看动画吧。 |
73 | 73 |
|
74 | 74 |
|
75 | 75 |
|
| 76 | +看完视频,是不是感觉自己搞懂了,又感觉自己没搞懂,哈哈,咱们继续往下看。 |
| 77 | + |
| 78 | +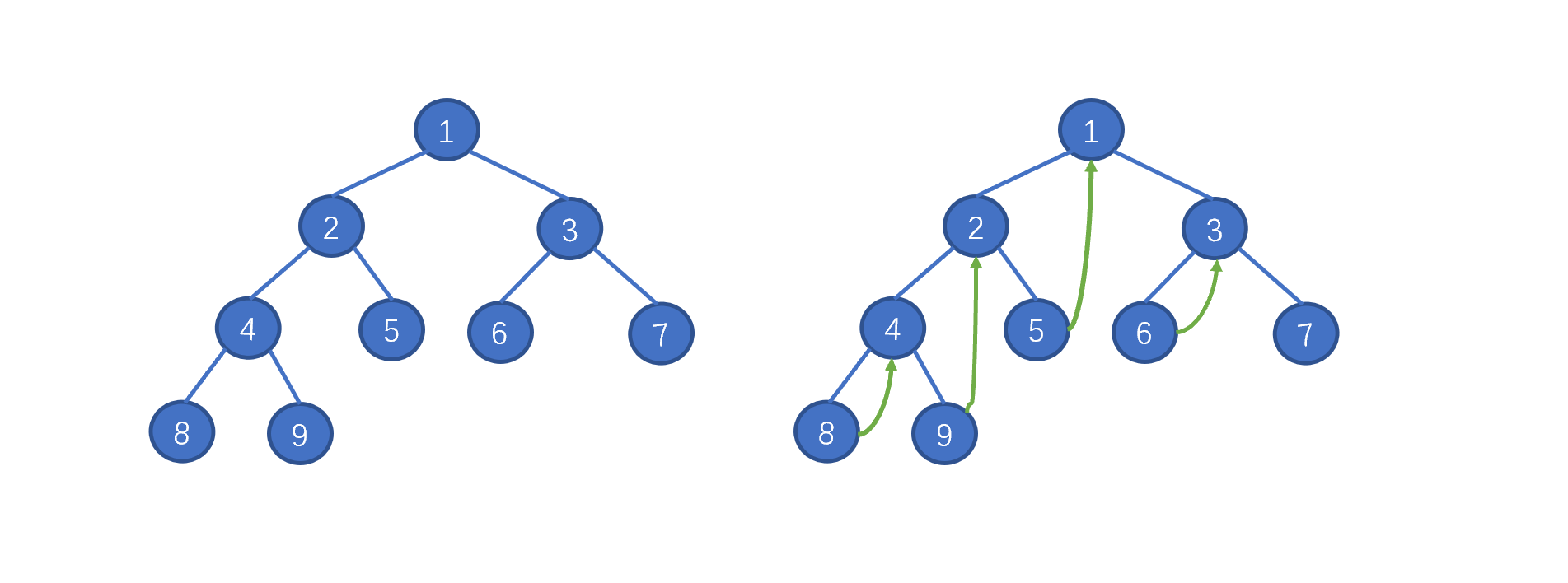 |
| 79 | + |
| 80 | +我们之前说的,Morris 遍历利用了`树中大量空闲指针的特性`,我们需要`找到当前节点的左子树中的最右边的叶子节点`,将该叶子节点的 right 指向当前节点。例如当前节点为2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。 |
| 81 | + |
| 82 | +其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。 |
| 83 | + |
| 84 | +1. 当 p1.left == null 时,p1 = p1.right。(这也就是我们为什么要给叶子节点添加 right 指针的原因) |
| 85 | + |
| 86 | +2. 如果 p1.left != null,找到 p1 左子树上最右的节点。(也就是我们的 p2 最后停留的位置),此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况。 |
| 87 | + |
| 88 | +3. - 如果 p2 的 right 指针指向空,让其指向 p1,p1向左移动,即 p1 = p1.left |
| 89 | + - 如果 p2 的 right 指针指向 p1,让其指向空,(为了防止重复执行,则需要去掉 right 指针)p1 向右移动,p1 = p1.right。 |
| 90 | + |
| 91 | +这时你可以结合咱们刚才提到的两个原则,再去看一遍动画,并代入规则进行模拟,差不多就能完全搞懂啦。 |
| 92 | + |
| 93 | +下面我们来对动画中的内容进行拆解 , |
| 94 | + |
| 95 | +首先 p1 指向 root节点 |
| 96 | + |
| 97 | +p2 = p1.left,下面我们需要通过 p2 找到 p1的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。 |
| 98 | + |
| 99 | +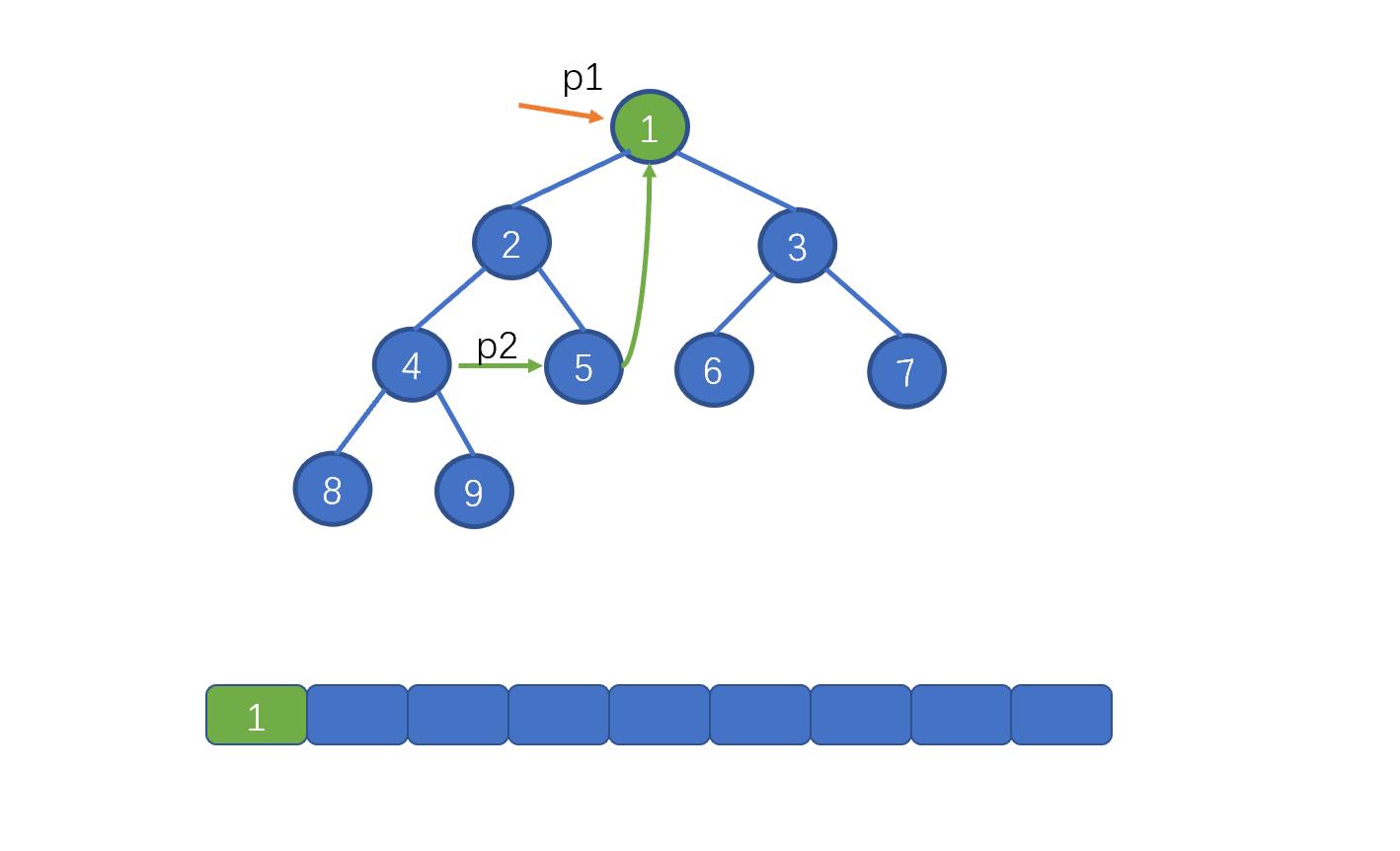 |
| 100 | + |
| 101 | +向左移动 p1,即 p1 = p1.left |
| 102 | + |
| 103 | +p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,也就是 9,并将该节点的 right 指针指向 2。 |
| 104 | + |
| 105 | +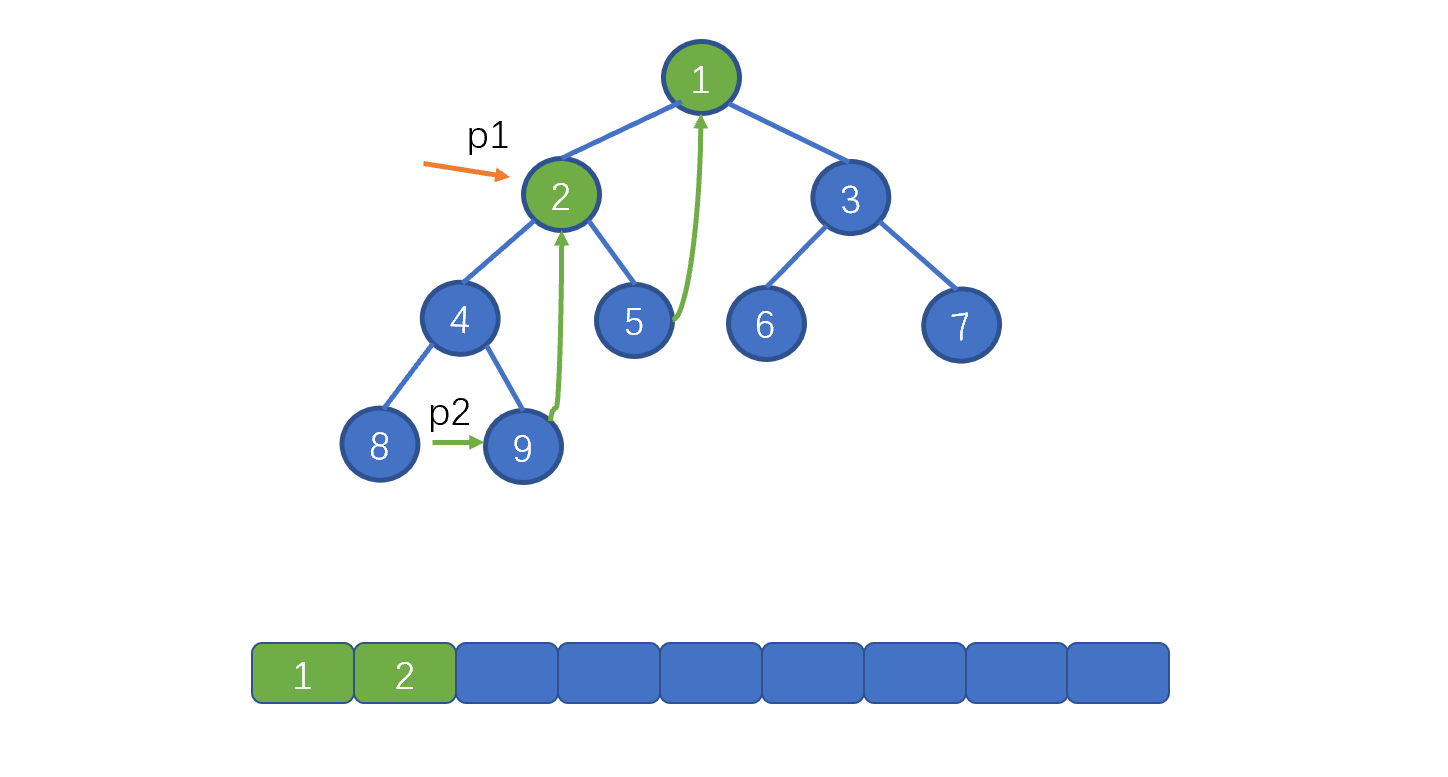 |
| 106 | + |
| 107 | + |
| 108 | + |
| 109 | +继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。 |
| 110 | + |
| 111 | +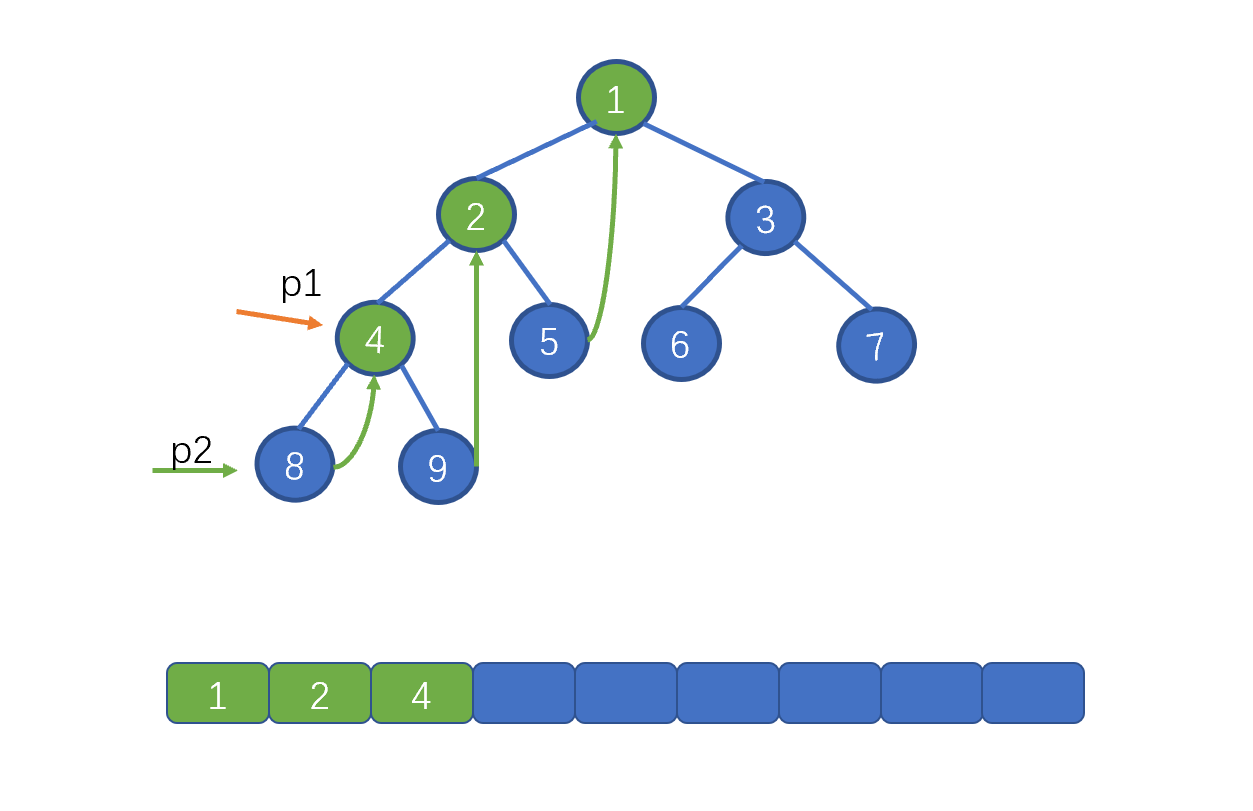 |
| 112 | + |
| 113 | + |
| 114 | + |
| 115 | +我们发现这一步给前两步是一样的,都是找到叶子节点,将其 right 指针指向 p1,此时我们完成了添加 right 指针的过程,下面我们继续往下看。 |
| 116 | + |
| 117 | +我们继续移动 p1 指针,p1 = p1.left。p2 = p.left。此时我们发现 p2 == null,即下图 |
| 118 | + |
| 119 | +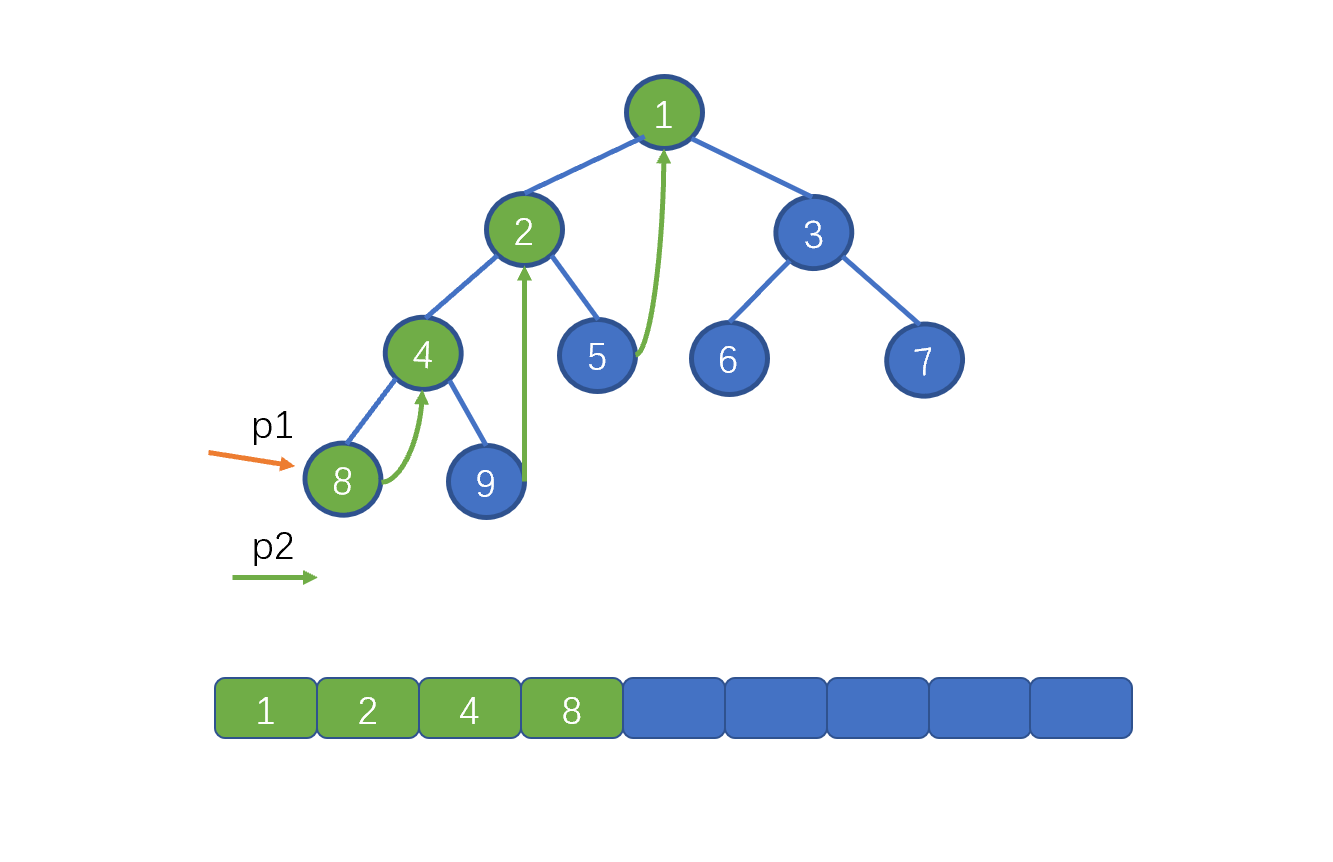 |
| 120 | + |
| 121 | +此时我们需要移动 p1, 但是不再是 p1 = p1.left 而是 p1 = p1.right。也就是 4,继续让 p2 = p1.left。此时则为下图这种情况 |
| 122 | + |
| 123 | +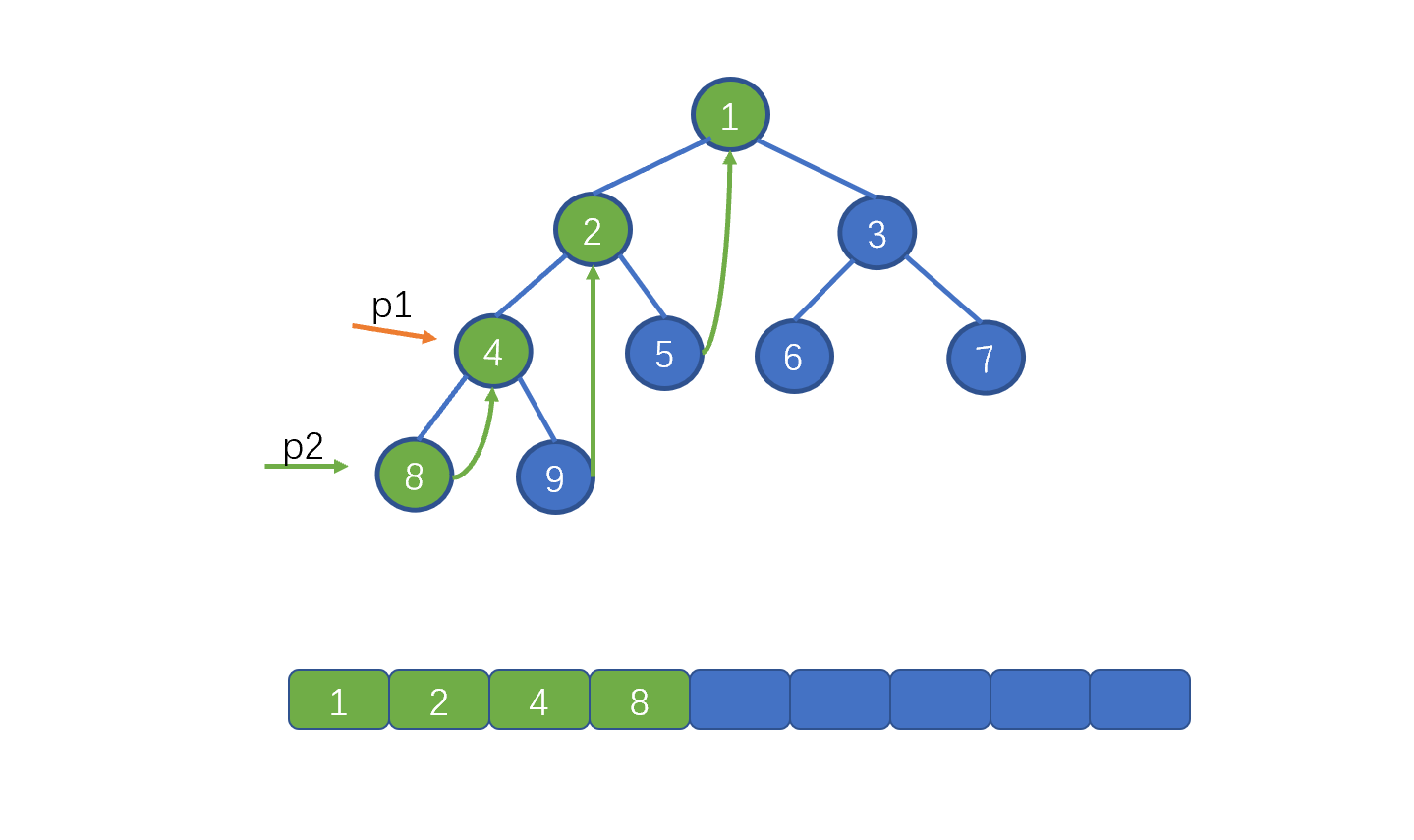 |
| 124 | + |
| 125 | +此时我们发现 p2.right != null 而是指向 4,说明此时我们已经添加过了 right 指针,所以去掉 right 指针,并让 p1 = p1.right |
| 126 | + |
| 127 | +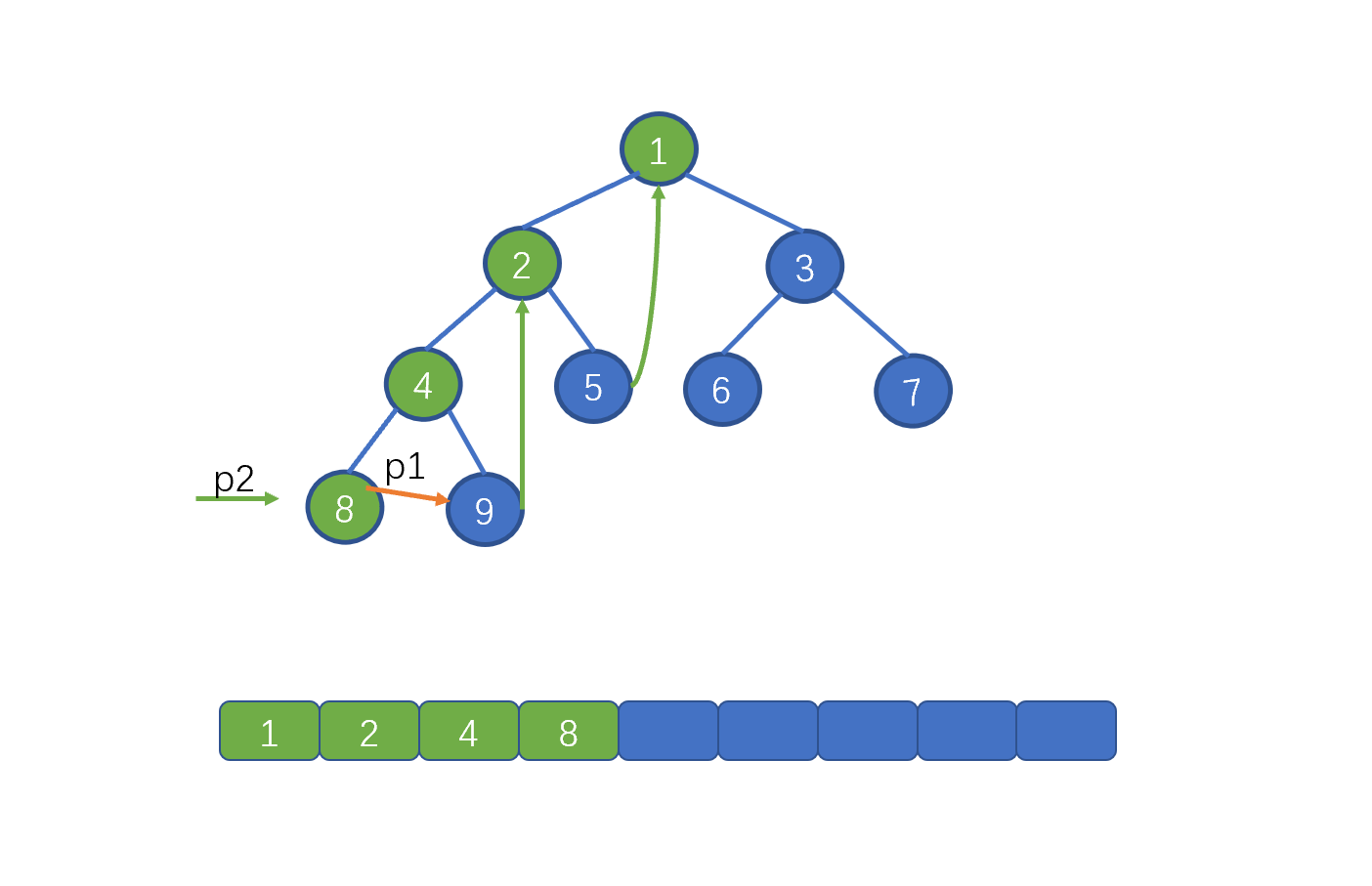 |
| 128 | + |
| 129 | +下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。 |
| 130 | + |
| 131 | +时间复杂度 O(n),空间复杂度 O(1) |
| 132 | + |
| 133 | +下面我们来看代码吧。 |
| 134 | + |
| 135 | +#### 代码 |
| 136 | + |
| 137 | +```java |
| 138 | +class Solution { |
| 139 | + public List<Integer> preorderTraversal(TreeNode root) { |
| 140 | + |
| 141 | + List<Integer> list = new ArrayList<>(); |
| 142 | + if (root == null) { |
| 143 | + return list; |
| 144 | + } |
| 145 | + TreeNode p1 = root; TreeNode p2 = null; |
| 146 | + while (p1 != null) { |
| 147 | + p2 = p1.left; |
| 148 | + if (p2 != null) { |
| 149 | + //找到左子树的最右叶子节点 |
| 150 | + while (p2.right != null && p2.right != p1) { |
| 151 | + p2 = p2.right; |
| 152 | + } |
| 153 | + //添加 right 指针,对应 right 指针为 null 的情况 |
| 154 | + if (p2.right == null) { |
| 155 | + list.add(p1.val); |
| 156 | + p2.right = p1; |
| 157 | + p1 = p1.left; |
| 158 | + continue; |
| 159 | + } |
| 160 | + //对应 right 指针存在的情况,则去掉 right 指针 |
| 161 | + p2.right = null; |
| 162 | + } else { |
| 163 | + list.add(p1.val); |
| 164 | + } |
| 165 | + //移动 p1 |
| 166 | + p1 = p1.right; |
| 167 | + } |
| 168 | + return list; |
| 169 | + } |
| 170 | +} |
| 171 | +``` |
| 172 | + |
| 173 | +好啦,今天就看到这里吧,咱们下期见! |
0 commit comments