|
| 1 | +之前给大家介绍了二叉树的[前序遍历](),[中序遍历]()的迭代法和 Morris 方法,今天咱们来说一下二叉后序遍历的迭代法及 Morris 方法。 |
| 2 | + |
| 3 | +注:阅读该文章前,建议各位先阅读之前的三篇文章,对该文章的理解有很大帮助。 |
| 4 | + |
| 5 | +## 迭代 |
| 6 | + |
| 7 | +后序遍历的相比前两种方法,难理解了一些,所以这里我们需要认真思考一下,每一行的代码的作用。 |
| 8 | + |
| 9 | +我们先来复习一下,二叉树的后序遍历 |
| 10 | + |
| 11 | +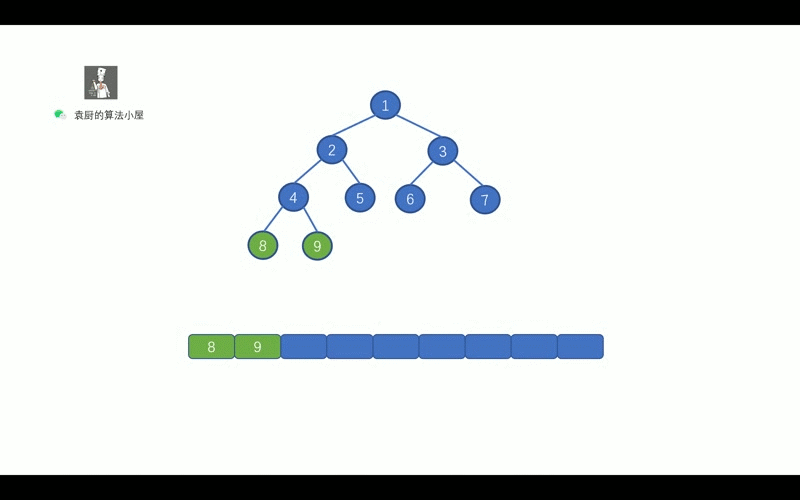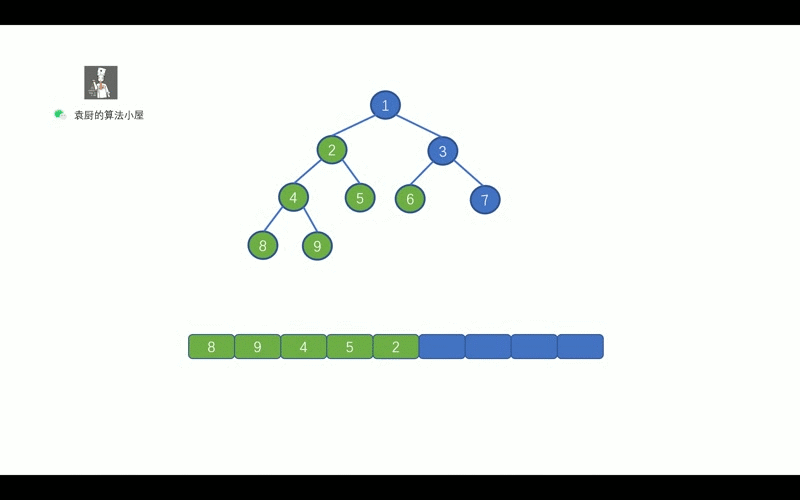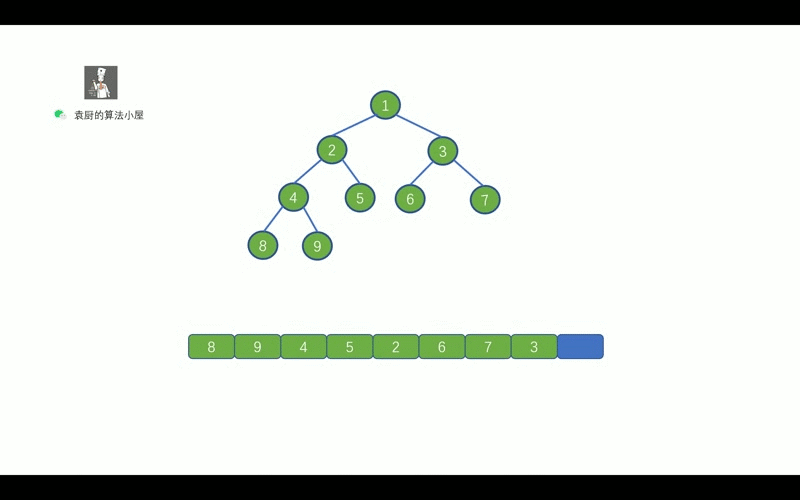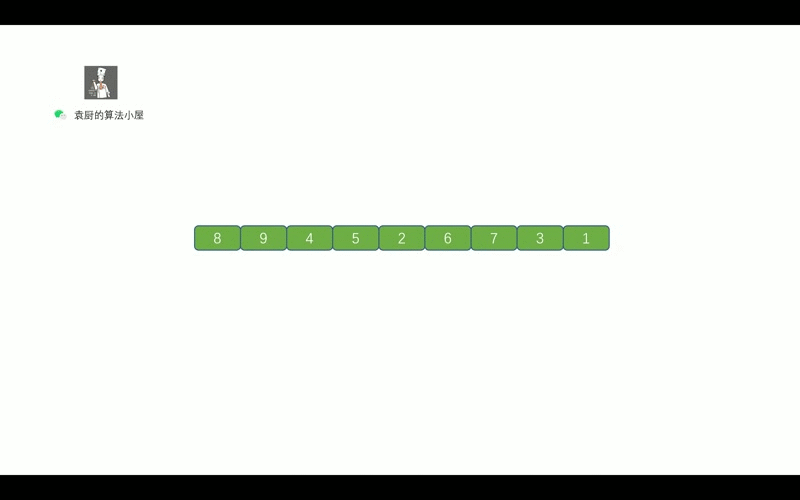 |
| 12 | + |
| 13 | +我们知道后序遍历的顺序是,` 对于树中的某节点, 先遍历该节点的左子树, 再遍历其右子树, 最后遍历该节点`。 |
| 14 | + |
| 15 | +那么我们如何利用栈来解决呢? |
| 16 | + |
| 17 | +我们直接来看动画,看动画之前,但是我们`需要带着问题看动画`,问题搞懂之后也就搞定了后序遍历。 |
| 18 | + |
| 19 | +1.动画中的橙色指针发挥了什么作用 |
| 20 | + |
| 21 | +2.为什么动画中的某节点,为什么出栈后又入栈呢? |
| 22 | + |
| 23 | +好啦,下面我们看动画吧! |
| 24 | + |
| 25 | +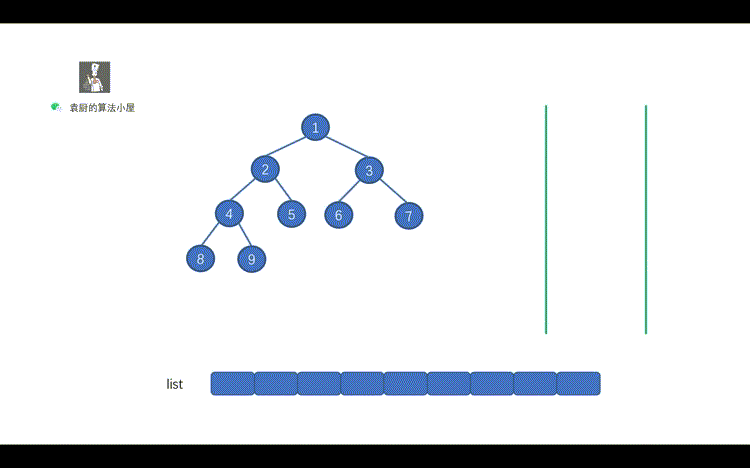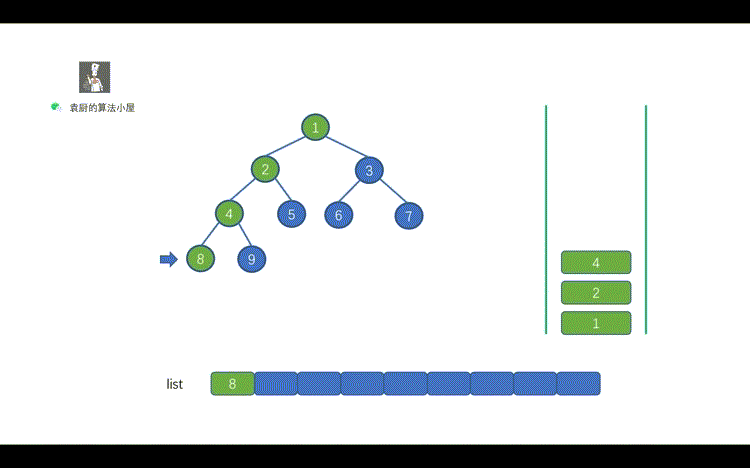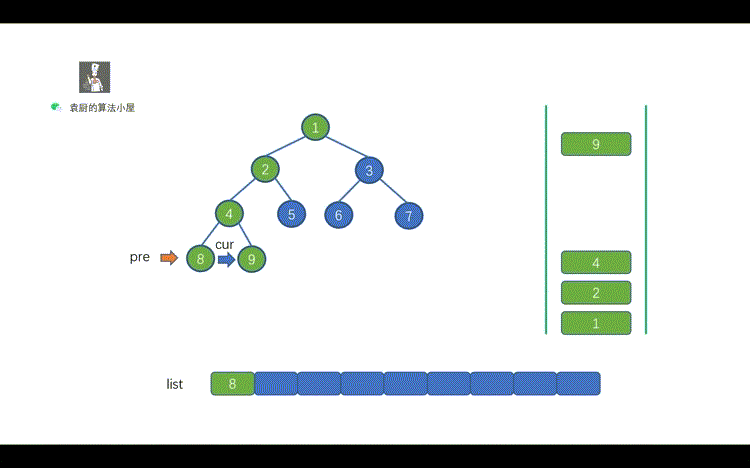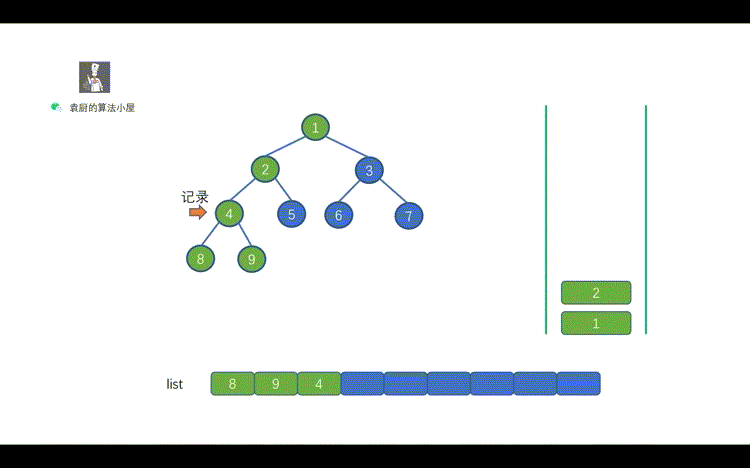 |
| 26 | + |
| 27 | +相信大家看完动画之后,也能够发现其中规律。 |
| 28 | + |
| 29 | +我们来对其中之前提出的问题进行解答 |
| 30 | + |
| 31 | +1.动画中的橙色箭头的作用? |
| 32 | + |
| 33 | +> 用来定位住上一个访问节点,这样我们就知道 cur 节点的 right 节点是否被访问,如果被访问,我们则需要遍历 cur 节点。 |
| 34 | +
|
| 35 | +2.为什么有的节点出栈后又入栈了呢? |
| 36 | + |
| 37 | +> 出栈又入栈的原因是,我们发现 cur 节点的 right 不为 null ,并且 cur.right 也没有被访问过。因为 `cur.right != preNode `,所以当前我们还不能够遍历该节点,应该先遍历其右子树中的节点。 |
| 38 | +> |
| 39 | +> 所以我们将其入栈后,然后`cur = cur.right` |
| 40 | +
|
| 41 | +```java |
| 42 | +class Solution { |
| 43 | + public List<Integer> postorderTraversal(TreeNode root) { |
| 44 | + Stack<TreeNode> stack = new Stack<>(); |
| 45 | + List<Integer> list = new ArrayList<>(); |
| 46 | + TreeNode cur = root; |
| 47 | + //这个用来记录前一个访问的节点,也就是橙色箭头 |
| 48 | + TreeNode preNode = null; |
| 49 | + while (cur != null || !stack.isEmpty()) { |
| 50 | + //和之前写的中序一致 |
| 51 | + while (cur != null) { |
| 52 | + stack.push(cur); |
| 53 | + cur = cur.left; |
| 54 | + } |
| 55 | + //1.出栈,可以想一下,这一步的原因。 |
| 56 | + cur = stack.pop(); |
| 57 | + //2.if 里的判断语句有什么含义? |
| 58 | + if (cur.right == null || cur.right == preNode) { |
| 59 | + list.add(cur.val); |
| 60 | + //更新下 preNode,也就是定位住上一个访问节点。 |
| 61 | + preNode = cur; |
| 62 | + cur = null; |
| 63 | + } else { |
| 64 | + //3.再次压入栈,和上面那条 1 的关系? |
| 65 | + stack.push(cur); |
| 66 | + cur = cur.right; |
| 67 | + } |
| 68 | + } |
| 69 | + return list; |
| 70 | + } |
| 71 | +} |
| 72 | +``` |
| 73 | + |
| 74 | +当然也可以修改下代码逻辑将 `cur = stack.pop()` 改成 `cur = stack.peek()`,下面再修改一两行代码也可以实现,这里这样写是方便动画模拟,大家可以随意发挥。 |
| 75 | + |
| 76 | +时间复杂度 O(n), 空间复杂度O(n) |
| 77 | + |
| 78 | +这里二叉树的三种迭代方式到这里就结束啦,大家可以进行归纳总结,三种遍历方式大同小异,建议各位,掌握之后,自己手撕一下,从搭建二叉树开始。 |
| 79 | + |
| 80 | +另外大家也可以看下 Carl 哥的这篇文章,迭代遍历的另一种实现方式。 |
| 81 | + |
| 82 | +> https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/bang-ni-dui-er-cha-shu-bu-zai-mi-mang-che-di-chi-t/ |
| 83 | +
|
| 84 | +好啦,下面我们看下后序遍历的 Morris 方法。 |
| 85 | + |
| 86 | +## Morris |
| 87 | + |
| 88 | +后序遍历的 Morris 方法也比之前两种代码稍微长一些,看着挺唬人,其实不难,和我们之前说的没差多少。下面我们一起来干掉它吧。 |
| 89 | + |
| 90 | +我们先来复习下之前说过的[中序遍历](),见下图。 |
| 91 | + |
| 92 | +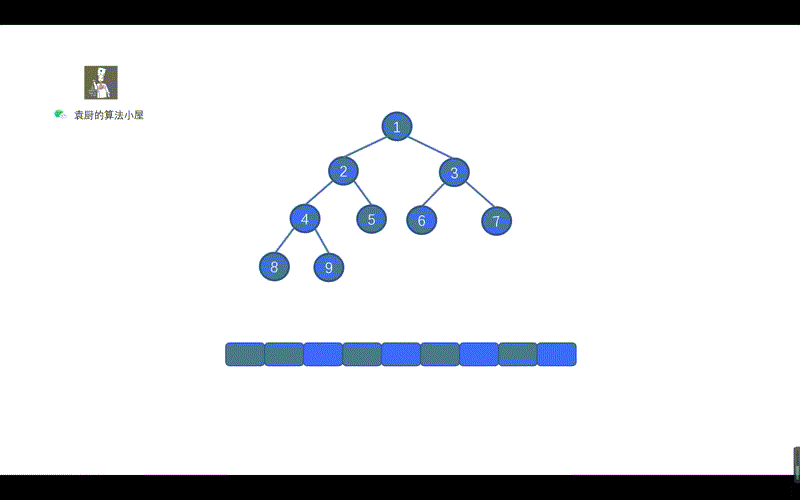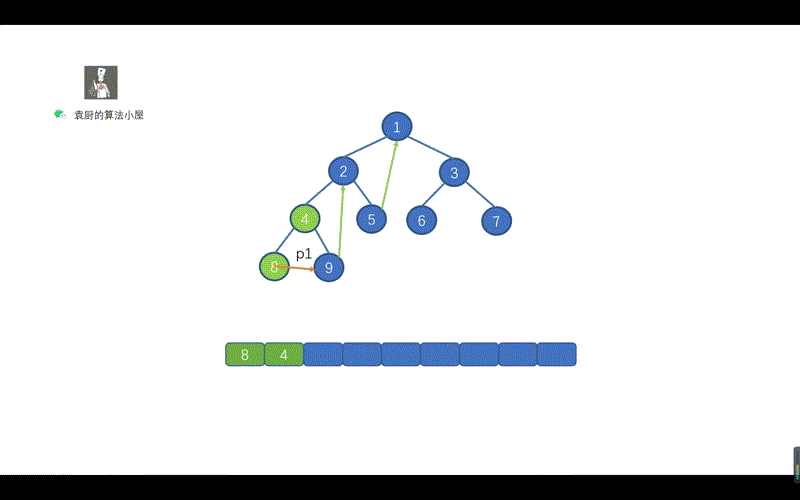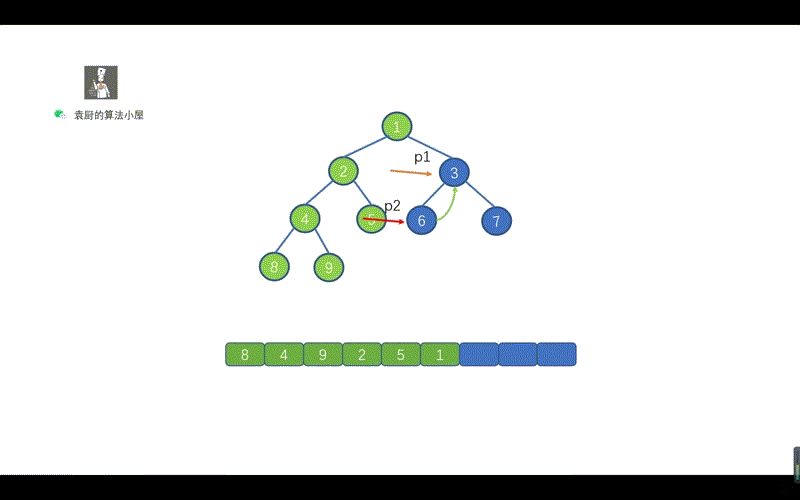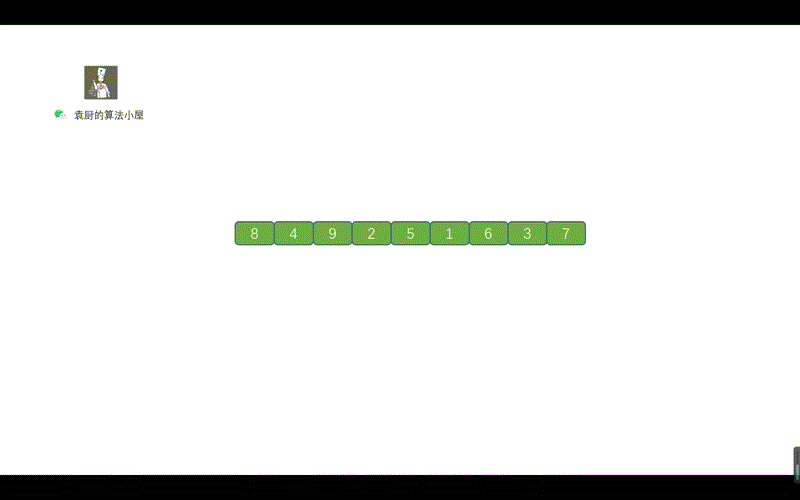 |
| 93 | + |
| 94 | +另外我们来对比下,中序遍历和后序遍历的 Morris 方法,代码有哪里不同。 |
| 95 | + |
| 96 | + |
| 97 | + |
| 98 | +由上图可知,仅仅有三处不同,后序遍历里少了 `list.add()`,多了一个函数` postMorris() ` ,那后序遍历的 list.add() 肯定是在 postMorris 函数中的。所以我们搞懂了 postMorris 函数,也就搞懂了后序遍历的 Morris 方法(默认大家看了之前的文章,没有看过的同学,可以点击文首的链接) |
| 99 | + |
| 100 | +下面我们一起来剖析下 postMorris 函数.代码如下 |
| 101 | + |
| 102 | +```java |
| 103 | +public void postMorris(TreeNode root) { |
| 104 | + //反转转链表,详情看下方图片 |
| 105 | + TreeNode reverseNode = reverseList(root); |
| 106 | + //遍历链表 |
| 107 | + TreeNode cur = reverseNode; |
| 108 | + while (cur != null) { |
| 109 | + list.add(cur.val); |
| 110 | + cur = cur.right; |
| 111 | + } |
| 112 | + //反转回来 |
| 113 | + reverseList(reverseNode); |
| 114 | + } |
| 115 | + |
| 116 | +//反转链表 |
| 117 | +public TreeNode reverseList(TreeNode head) { |
| 118 | + TreeNode cur = head; |
| 119 | + TreeNode pre = null; |
| 120 | + while (cur != null) { |
| 121 | + TreeNode next = cur.right; |
| 122 | + cur.right = pre; |
| 123 | + pre = cur; |
| 124 | + cur = next; |
| 125 | + } |
| 126 | + return pre; |
| 127 | + } |
| 128 | +``` |
| 129 | + |
| 130 | +上面的代码,是不是贼熟悉,和我们的倒序输出链表一致,步骤为,反转链表,遍历链表,将链表反转回原样。只不过我们将 ListNode.next 写成了 TreeNode.right 将树中的遍历右子节点的路线,看成了一个链表,见下图。 |
| 131 | + |
| 132 | +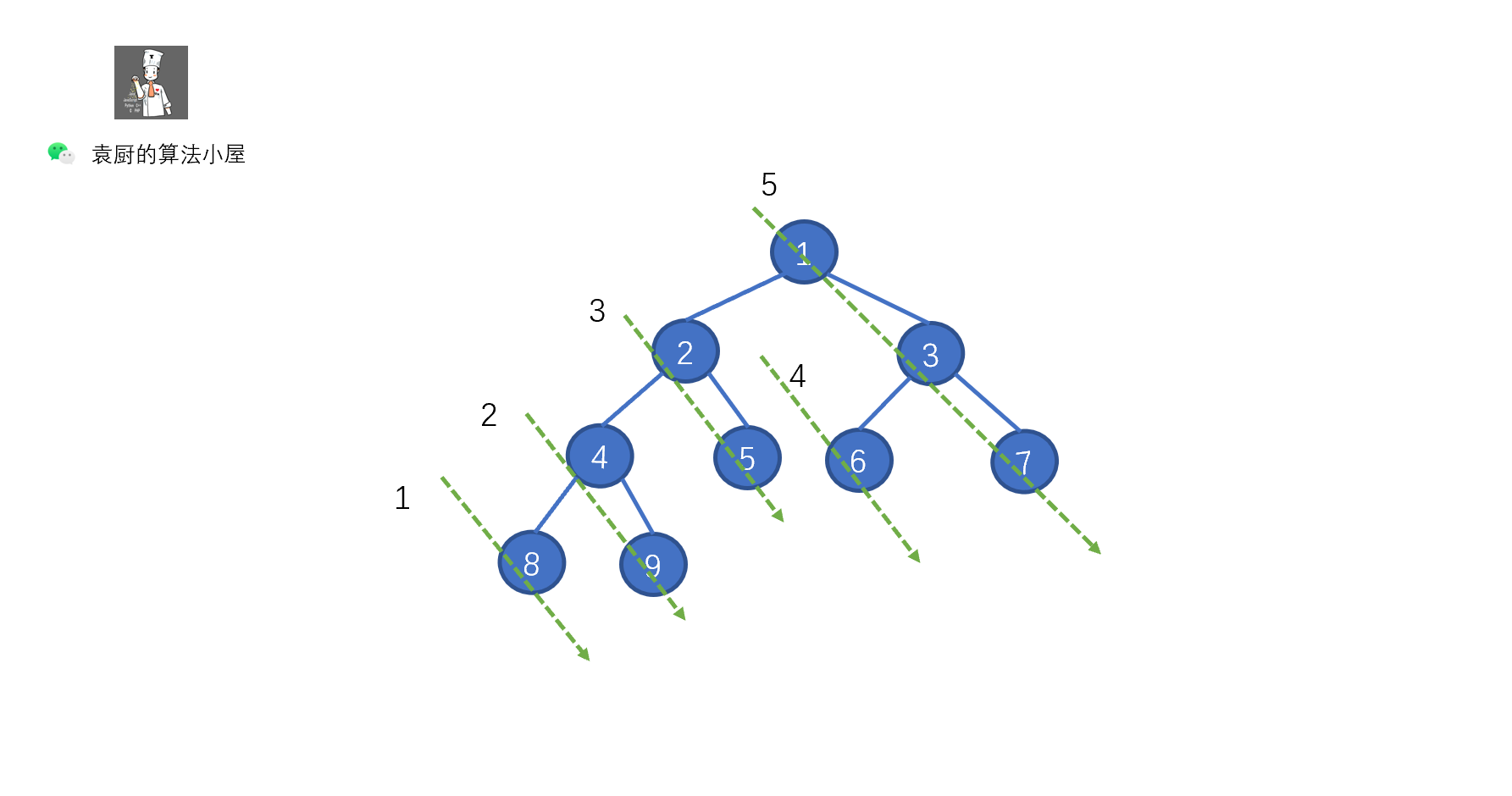 |
| 133 | + |
| 134 | +上图中的一个绿色虚线,代表一个链表,我们根据序号进行倒序遍历,看下是什么情况 |
| 135 | + |
| 136 | +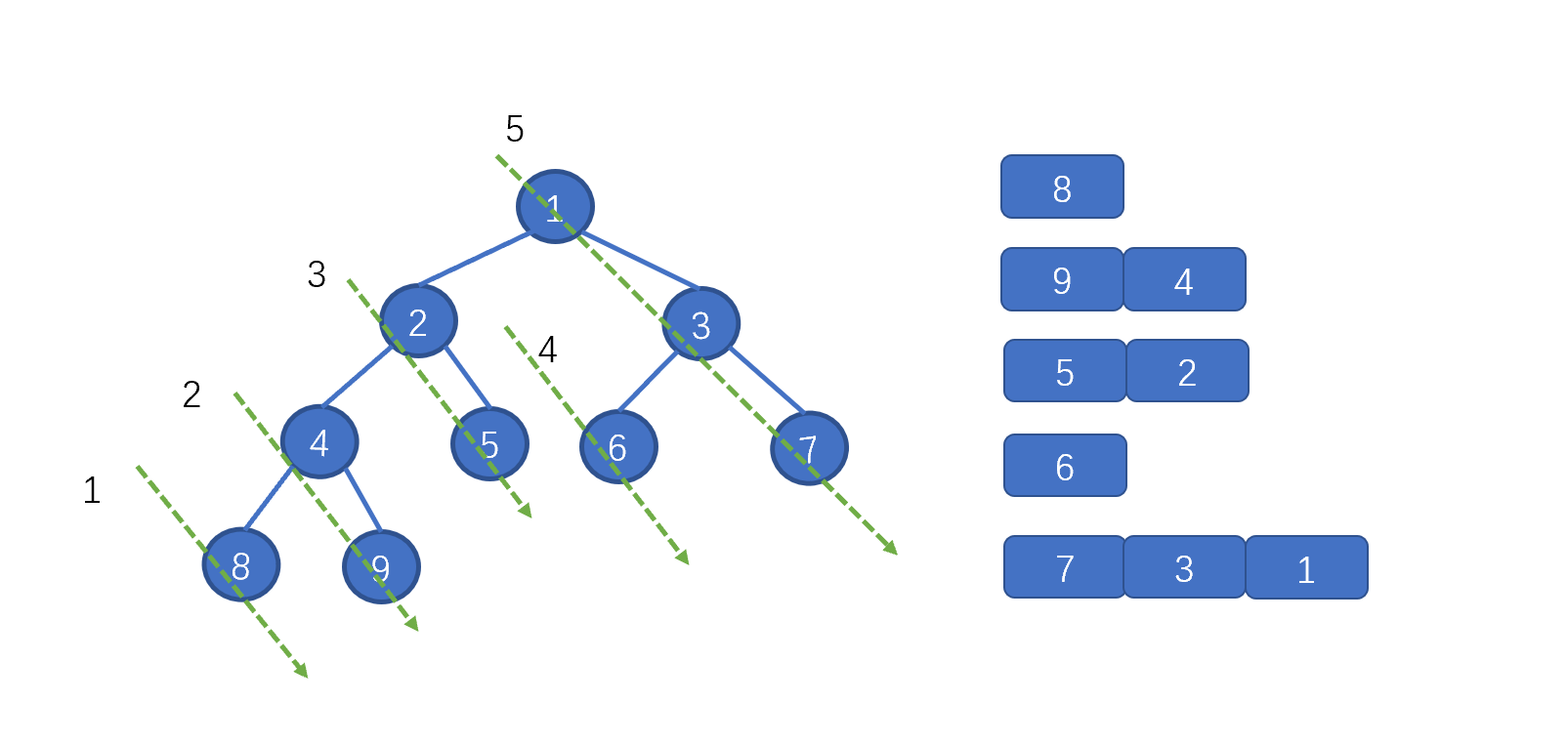 |
| 137 | + |
| 138 | + |
| 139 | + |
| 140 | +到这块是不是就整懂啦,打完收工! |
| 141 | + |
| 142 | +```java |
| 143 | +class Solution { |
| 144 | + List<Integer> list; |
| 145 | + public List<Integer> postorderTraversal(TreeNode root) { |
| 146 | + list = new ArrayList<>(); |
| 147 | + if (root == null) { |
| 148 | + return list; |
| 149 | + } |
| 150 | + TreeNode p1 = root; |
| 151 | + TreeNode p2 = null; |
| 152 | + while (p1 != null) { |
| 153 | + p2 = p1.left; |
| 154 | + if (p2 != null) { |
| 155 | + while (p2.right != null && p2.right != p1) { |
| 156 | + p2 = p2.right; |
| 157 | + } |
| 158 | + if (p2.right == null) { |
| 159 | + p2.right = p1; |
| 160 | + p1 = p1.left; |
| 161 | + continue; |
| 162 | + } else { |
| 163 | + p2.right = null; |
| 164 | + postMorris(p1.left); |
| 165 | + } |
| 166 | + } |
| 167 | + p1 = p1.right; |
| 168 | + } |
| 169 | + //以根节点为起点的链表 |
| 170 | + postMorris(root); |
| 171 | + return list; |
| 172 | + } |
| 173 | + public void postMorris(TreeNode root) { |
| 174 | + //翻转链表 |
| 175 | + TreeNode reverseNode = reverseList(root); |
| 176 | + //从后往前遍历 |
| 177 | + TreeNode cur = reverseNode; |
| 178 | + while (cur != null) { |
| 179 | + list.add(cur.val); |
| 180 | + cur = cur.right; |
| 181 | + } |
| 182 | + //翻转回来 |
| 183 | + reverseList(reverseNode); |
| 184 | + } |
| 185 | + public TreeNode reverseList(TreeNode head) { |
| 186 | + TreeNode cur = head; |
| 187 | + TreeNode pre = null; |
| 188 | + while (cur != null) { |
| 189 | + TreeNode next = cur.right; |
| 190 | + cur.right = pre; |
| 191 | + pre = cur; |
| 192 | + cur = next; |
| 193 | + } |
| 194 | + return pre; |
| 195 | + } |
| 196 | + |
| 197 | +} |
| 198 | +``` |
| 199 | + |
| 200 | +时间复杂度 O(n)空间复杂度 O(1) |
| 201 | + |
| 202 | +总结:后序遍历比起前序和中序稍微复杂了一些,所以我们解题的时候,需要好好注意一下,迭代法的核心是利用一个指针来定位我们上一个遍历的节点,Morris 的核心是,将某节点的右子节点,看成是一条链表,进行反向遍历。 |
| 203 | + |
| 204 | +好啦,今天就唠到这吧,拜了个拜。 |
| 205 | + |
| 206 | + |
| 207 | + |
0 commit comments