|
| 1 | +## 题目地址 (947. 移除最多的同行或同列石头) |
| 2 | + |
| 3 | +https://leetcode-cn.com/problems/most-stones-removed-with-same-row-or-column/ |
| 4 | + |
| 5 | +## 题目描述 |
| 6 | + |
| 7 | +``` |
| 8 | +n 块石头放置在二维平面中的一些整数坐标点上。每个坐标点上最多只能有一块石头。 |
| 9 | +
|
| 10 | +如果一块石头的 同行或者同列 上有其他石头存在,那么就可以移除这块石头。 |
| 11 | +
|
| 12 | +给你一个长度为 n 的数组 stones ,其中 stones[i] = [xi, yi] 表示第 i 块石头的位置,返回 可以移除的石子 的最大数量。 |
| 13 | +
|
| 14 | + |
| 15 | +
|
| 16 | +示例 1: |
| 17 | +
|
| 18 | +输入:stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]] |
| 19 | +输出:5 |
| 20 | +解释:一种移除 5 块石头的方法如下所示: |
| 21 | +1. 移除石头 [2,2] ,因为它和 [2,1] 同行。 |
| 22 | +2. 移除石头 [2,1] ,因为它和 [0,1] 同列。 |
| 23 | +3. 移除石头 [1,2] ,因为它和 [1,0] 同行。 |
| 24 | +4. 移除石头 [1,0] ,因为它和 [0,0] 同列。 |
| 25 | +5. 移除石头 [0,1] ,因为它和 [0,0] 同行。 |
| 26 | +石头 [0,0] 不能移除,因为它没有与另一块石头同行/列。 |
| 27 | +示例 2: |
| 28 | +
|
| 29 | +输入:stones = [[0,0],[0,2],[1,1],[2,0],[2,2]] |
| 30 | +输出:3 |
| 31 | +解释:一种移除 3 块石头的方法如下所示: |
| 32 | +1. 移除石头 [2,2] ,因为它和 [2,0] 同行。 |
| 33 | +2. 移除石头 [2,0] ,因为它和 [0,0] 同列。 |
| 34 | +3. 移除石头 [0,2] ,因为它和 [0,0] 同行。 |
| 35 | +石头 [0,0] 和 [1,1] 不能移除,因为它们没有与另一块石头同行/列。 |
| 36 | +示例 3: |
| 37 | +
|
| 38 | +输入:stones = [[0,0]] |
| 39 | +输出:0 |
| 40 | +解释:[0,0] 是平面上唯一一块石头,所以不可以移除它。 |
| 41 | + |
| 42 | +
|
| 43 | +提示: |
| 44 | +
|
| 45 | +1 <= stones.length <= 1000 |
| 46 | +0 <= xi, yi <= 104 |
| 47 | +不会有两块石头放在同一个坐标点上 |
| 48 | +
|
| 49 | +``` |
| 50 | + |
| 51 | +## 前置知识 |
| 52 | + |
| 53 | +- [并查集](https://github.com/azl397985856/leetcode/blob/master/thinkings/union-find.md) |
| 54 | + |
| 55 | +## 思路 |
| 56 | + |
| 57 | +读完题目之后, 看了下数据范围。我猜测可能和动态规划什么的有关,**而且时间复杂度是 $O(n^2)$ 左右**,其中 n 为 stones 的长度。继续看了下示例,然后跟着思考了一下,发现很像是某种联通关系。 类似的题目有很多,题目描述记不太清楚了。大概意思是给你一个二维网格,行和列需要**一起增加**,求最小和什么的。这类题目都是行和列具有某种绑定关系。 于是我想到了使用并查集来做。 后面想了一下,反正就是**求联通区域的个数**,因此使用 DFS 和 BFS 都可以。如果你想使用 DFS 或者 BFS 来解,可以结合我之前写的 [小岛专题](https://github.com/azl397985856/leetcode/blob/master/thinkings/island.md) 练习一下哦。 |
| 58 | + |
| 59 | +继续分析下题目。 题目的意思是任意一个石头可以消除和它同行和同列的其他石子。于是我就想象出了下面这样一幅图,其中红色的方块表示石子,方块的连线表示离得最近的可以消除的石子。实际上,一个石子除了可以消除图中线条直接相连的石子,还可以消除邻居的邻居。**这提示我们使用并查集维护这种联通关系**,联通的依据自然就是列或者行一样。 |
| 60 | + |
| 61 | +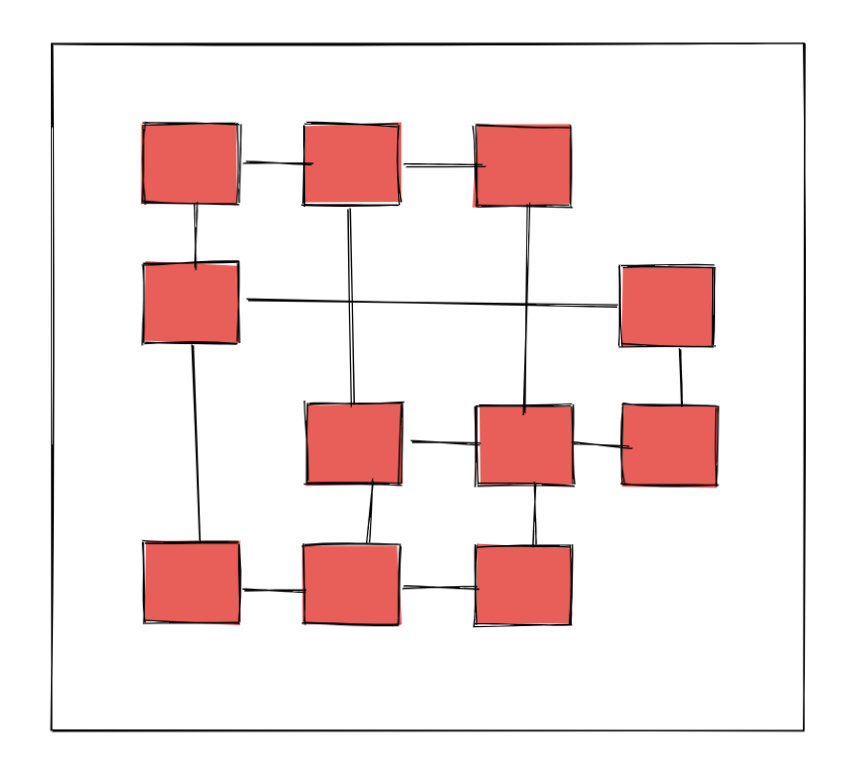 |
| 62 | + |
| 63 | +上面是一个全联通的图。如下是有两个联通域的图。 |
| 64 | + |
| 65 | +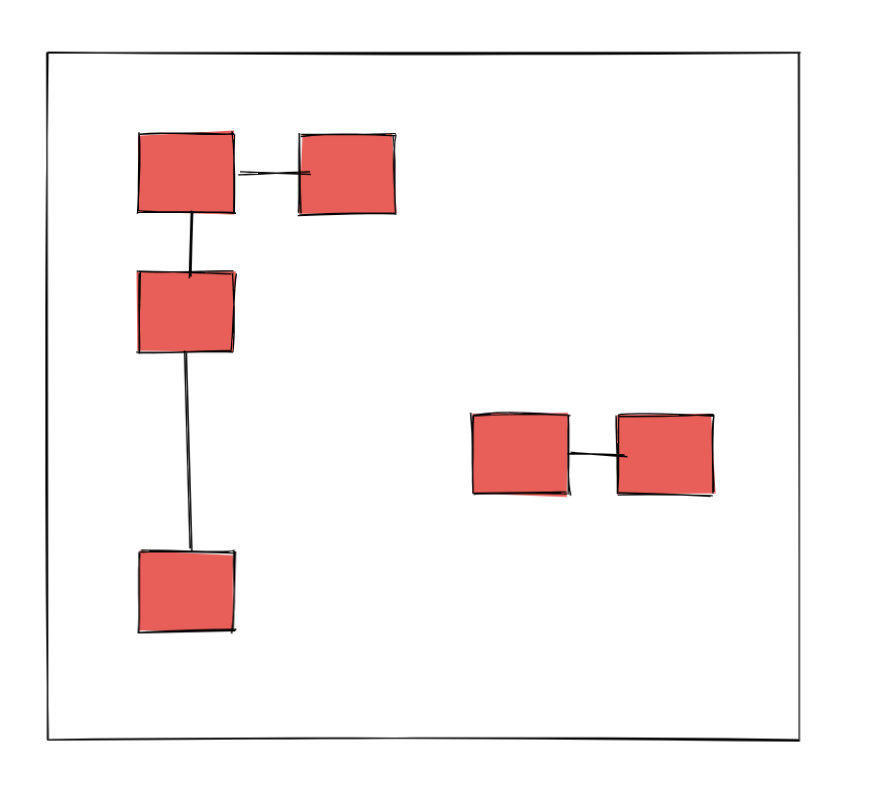 |
| 66 | + |
| 67 | +有了上面的知识,其实就可以将石子全部建立并查集的联系,并计算联通子图的个数。答案就是 n - 联通子图的个数,其中 n 为 stones 的长度。 |
| 68 | + |
| 69 | +核心代码: |
| 70 | + |
| 71 | +```py |
| 72 | +n = len(stones) |
| 73 | +# 标准并查集模板 |
| 74 | +uf = UF(n) |
| 75 | +# 两个 for 循环作用是将所有石子两两合并 |
| 76 | +for i in range(n): |
| 77 | + for j in range(i + 1, n): |
| 78 | + # 如果行或者列相同,将其联通成一个子图 |
| 79 | + if stones[i][0] == stones[j][0] or stones[i][1] == stones[j][1]: uf.union(i, j) |
| 80 | +return n - uf.cnt |
| 81 | +``` |
| 82 | + |
| 83 | +有的人想问,这可行么?即**我可以将一个联通子图的石子移除只剩下一个么?** |
| 84 | + |
| 85 | +答案是肯定的。其实上面我提到了这道题也可使用 DFS 和 BFS 的方式来做。如果你使用 DFS 的方式来做,会发现其实 **DFS 路径的取反就是消除的顺序**,当然消除的顺序不唯一,因为遍历访问联通子图的序列并不唯一。 如果题目要求我们求移除顺序,那我们可以考虑使用 DFS 来做,同时记录路径信息即可。 |
| 86 | + |
| 87 | +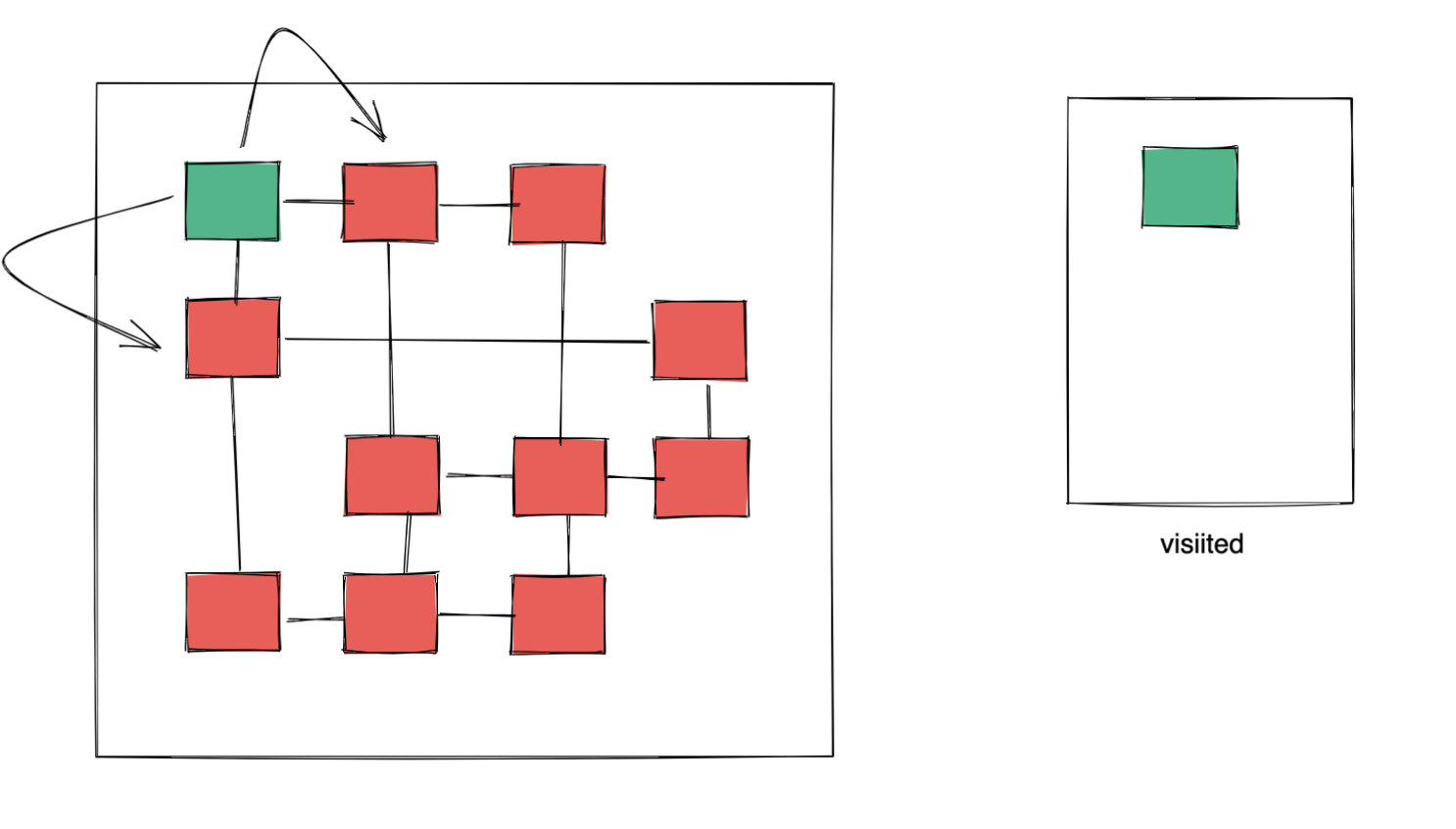 |
| 88 | + |
| 89 | +使用遍历的方式(BFS 或者 DFS),由于每次访问一个石子都需要使用 visited 来记录访问信息防止环的产生,因此 visited 的逆序也是一个可行的移除顺序。不过这要求你的 visited 的是有序的。实现的方法有很多,有点偏题了,这里就不赘述了。 |
| 90 | + |
| 91 | +实际上,上面的并查集代码仍然可以优化。上面的思路是直接将点作为并查集的联通条件。实际上,我们可以将点的横纵坐标分别作为联通条件。即如果横坐标相同的联通到一个子图,纵坐标相同的联通到一个子图。如下图: |
| 92 | + |
| 93 | + |
| 94 | + |
| 95 | +为了达到这个模板,我们不能再初始化的时候计算联通域数量了,即不能像上面那样 `uf = UF(n)`(此时联通域个数为 n)。因为横坐标,纵坐标分别有多少不重复的我们是不知道的,一种思路是先计算出**横坐标,纵坐标分别有多少不重复的**。这当然可以,还有一种思路是在 find 过程中计算,这样 one pass 即可完成,具体见下方代码区。 |
| 96 | + |
| 97 | +由于我们需要**区分横纵坐标**(上面图也可以看出来),因此可**用一种映射**区分二者。由于题目限定了横纵坐标取值为 10000 以内(包含 10000),一种思路就是将 x 或者 y 加上 10001。 |
| 98 | + |
| 99 | +核心代码: |
| 100 | + |
| 101 | +```py |
| 102 | +n = len(stones) |
| 103 | +uf = UF(0) |
| 104 | +for i in range(n): |
| 105 | + uf.union(stones[i][0] + 10001, stones[i][1]) |
| 106 | +return n - uf.cnt |
| 107 | +``` |
| 108 | + |
| 109 | +## 代码 |
| 110 | + |
| 111 | +### 并查集 |
| 112 | + |
| 113 | +代码支持: Python3 |
| 114 | + |
| 115 | +其中 `class UF` 部分是标准的无权并查集模板,我一行代码都没变。关于模板可以去 [并查集](https://github.com/azl397985856/leetcode/blob/master/thinkings/union-find.md) 查看。 |
| 116 | + |
| 117 | +```python |
| 118 | +class UF: |
| 119 | + def __init__(self, M): |
| 120 | + self.parent = {} |
| 121 | + self.cnt = 0 |
| 122 | + # 初始化 parent,size 和 cnt |
| 123 | + for i in range(M): |
| 124 | + self.parent[i] = i |
| 125 | + self.cnt += 1 |
| 126 | + |
| 127 | + def find(self, x): |
| 128 | + if x != self.parent[x]: |
| 129 | + self.parent[x] = self.find(self.parent[x]) |
| 130 | + return self.parent[x] |
| 131 | + return x |
| 132 | + def union(self, p, q): |
| 133 | + if self.connected(p, q): return |
| 134 | + leader_p = self.find(p) |
| 135 | + leader_q = self.find(q) |
| 136 | + self.parent[leader_p] = leader_q |
| 137 | + self.cnt -= 1 |
| 138 | + def connected(self, p, q): |
| 139 | + return self.find(p) == self.find(q) |
| 140 | + |
| 141 | +class Solution: |
| 142 | + def removeStones(self, stones: List[List[int]]) -> int: |
| 143 | + n = len(stones) |
| 144 | + uf = UF(n) |
| 145 | + for i in range(n): |
| 146 | + for j in range(i + 1, n): |
| 147 | + if stones[i][0] == stones[j][0] or stones[i][1] == stones[j][1]: uf.union(i, j) |
| 148 | + return n - uf.cnt |
| 149 | + |
| 150 | +``` |
| 151 | + |
| 152 | +**复杂度分析** |
| 153 | + |
| 154 | +令 n 为数组 stones 的长度。 |
| 155 | + |
| 156 | +- 时间复杂度:$O(n^2logn)$ |
| 157 | +- 空间复杂度:$O(n)$ |
| 158 | + |
| 159 | +### 优化的并查集 |
| 160 | + |
| 161 | +代码支持: Python3 |
| 162 | + |
| 163 | +```py |
| 164 | +class UF: |
| 165 | + def __init__(self, M): |
| 166 | + self.parent = {} |
| 167 | + self.cnt = 0 |
| 168 | + |
| 169 | + def find(self, x): |
| 170 | + if x not in self.parent: |
| 171 | + self.cnt += 1 |
| 172 | + self.parent[x] = x |
| 173 | + if x != self.parent[x]: |
| 174 | + self.parent[x] = self.find(self.parent[x]) |
| 175 | + return self.parent[x] |
| 176 | + return x |
| 177 | + def union(self, p, q): |
| 178 | + if self.connected(p, q): return |
| 179 | + leader_p = self.find(p) |
| 180 | + leader_q = self.find(q) |
| 181 | + self.parent[leader_p] = leader_q |
| 182 | + self.cnt -= 1 |
| 183 | + def connected(self, p, q): |
| 184 | + return self.find(p) == self.find(q) |
| 185 | + |
| 186 | +class Solution: |
| 187 | + def removeStones(self, stones: List[List[int]]) -> int: |
| 188 | + n = len(stones) |
| 189 | + uf = UF(0) |
| 190 | + for i in range(n): |
| 191 | + uf.union(stones[i][0] + 10001, stones[i][1]) |
| 192 | + return n - uf.cnt |
| 193 | +``` |
| 194 | + |
| 195 | +**复杂度分析** |
| 196 | + |
| 197 | +令 n 为数组 stones 的长度。 |
| 198 | + |
| 199 | +- 时间复杂度:$O(nlogn)$ |
| 200 | +- 空间复杂度:$O(n)$ |
| 201 | + |
| 202 | +### DFS |
| 203 | + |
| 204 | +代码支持: Java |
| 205 | + |
| 206 | +> by 一位不愿透露姓名的热心网友。 |
| 207 | +
|
| 208 | +```java |
| 209 | +public int removeStones(int[][] stones) { |
| 210 | + Set visit = new HashSet(); |
| 211 | + int count = 0; |
| 212 | + int offset = 10000; |
| 213 | + HashMap <Integer,List<int []>>map = new HashMap(); |
| 214 | + |
| 215 | + // 构造图 每一项是一个节点 |
| 216 | + for (int i = 0; i < stones.length; i++) { |
| 217 | + int [] node = stones[i]; |
| 218 | + List<int []> list = map.getOrDefault(node[0]-offset,new ArrayList<>()); |
| 219 | + list.add(node); |
| 220 | + map.put(node[0]-offset,list); |
| 221 | + |
| 222 | + List<int []> list1 = map.getOrDefault(node[1],new ArrayList<>()); |
| 223 | + list1.add(node); |
| 224 | + map.put(node[1],list1); |
| 225 | + } |
| 226 | + // 寻找联通分量 |
| 227 | + for (int i = 0; i < stones.length; i++) { |
| 228 | + int [] node = stones[i]; |
| 229 | + if (!visit.contains((node))){ |
| 230 | + visit.add((node)); |
| 231 | + dfs(node,visit,map); |
| 232 | + count++; |
| 233 | + } |
| 234 | + } |
| 235 | + return stones.length-count; |
| 236 | + } |
| 237 | + |
| 238 | + // 遍历节点 |
| 239 | + public void dfs(int[]node, Set set,HashMap <Integer,List<int []>>map){ |
| 240 | + int offset = 10000; |
| 241 | + List<int []> list = map.getOrDefault(node[0]-offset,new ArrayList<>()); |
| 242 | + for (int i = 0; i < list.size(); i++) { |
| 243 | + int[] item = list.get(i); |
| 244 | + if (!set.contains((item))){ |
| 245 | + set.add((item)); |
| 246 | + dfs(item,set,map); |
| 247 | + } |
| 248 | + } |
| 249 | + List<int []> list2 = map.getOrDefault(node[1],new ArrayList<>()); |
| 250 | + for (int i = 0; i < list2.size(); i++) { |
| 251 | + int[] item = list2.get(i); |
| 252 | + if (!set.contains((item))){ |
| 253 | + set.add((item)); |
| 254 | + dfs(item,set,map); |
| 255 | + } |
| 256 | + } |
| 257 | + } |
| 258 | +``` |
| 259 | + |
| 260 | +**复杂度分析** |
| 261 | + |
| 262 | +令 n 为数组 stones 的长度。 |
| 263 | + |
| 264 | +- 时间复杂度:建图和遍历图的时间均为 $O(n)$ |
| 265 | +- 空间复杂度:$O(n)$ |
| 266 | + |
| 267 | +力扣的小伙伴的点下我头像的关注按钮,这样就会第一时间收到我的动态啦~ |
| 268 | + |
| 269 | +以上就是本文的全部内容了。大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 38K star 啦。 |
0 commit comments