1. はじめに
過去60年にわたって、多くの研究者が様々な言語で自動翻訳の可能性を追究してきました。機械翻訳は学術的研究の関心の的だけでなく、国防、金融、コミュニケーションなど、さまざまな分野から注目を集めてきました。
今日、機械翻訳は多くのアプリケーションにおいて重要な役割を担っており、その最先端を行く方法の1つが、統計を用いた、統計的機械翻訳 (SMT) と呼ばれるものです。統計的機械翻訳は、Google翻訳、Microsoft Translator、オープンソースの機械翻訳システムMosesなど、多くの翻訳システムにおいて、最も広く用いられている技術です。
統計的機械翻訳においては、確率推定の精度が非常に高くないと、適切な翻訳が難しくなります。そのため、私たちはベイズの定理を用いて、翻訳の問題を、言語モデルと翻訳モデルの2つに切り分けます。しかしここでは、長さの制約上、その1つ目、言語モデルについての基本的な理論のみを取り上げることにします。
この記事では、1) 統計的機械翻訳の基になっている理論の概要、および 2) 統計的機械翻訳において広く用いられている言語モデル法、についての簡単な紹介を行います。
また、この記事の読者には、統計的機械翻訳に興味はあるものの、特に知識は持ち合わせていない方を想定しています。
2. 統計的機械翻訳の概要
2.1 統計的機械翻訳システム
統計的機械翻訳システムは、言語モデル、翻訳モデル、およびデコーダーの3つの基本的な構成要素を有します。これらの構成要素からなる単純なSMTシステムの例を図1に示します。この記事では、日本語を英語に翻訳するものとして説明を進めていきます。また、以後の説明文中の定義および数式においては、和文をf、英文をeで示します。
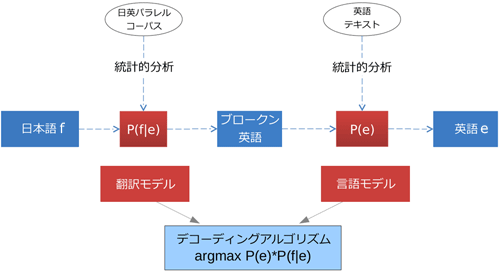
SMTシステムの動きをよりよく理解するために、実際の翻訳における例を示します。ウィーバー・ウォーレンは、翻訳を暗号法の問題の一種と捉えて、次のように述べています。
私の目の前にはロシア語の文があるが、私はこれを、変なシンボルでコーディングされた英語で書かれているものであるとみなす。ここで私がすべきことは、テキストで記された情報を受け取るために、コードを外すことである。
ここで述べられていることを例文にあてはめてみることにします。例えば、「ジョンはメアリーを愛している」という和文を英語に翻訳し、得たい英文が“John loves Mary.”であるとします。その場合、ここで述べられていることからは、私たちはまず英文“John loves Mary.”があって、しかし紙に記載された時点では、この文はコーディングされ、「ジョンはメアリーを愛している」という和文になっていると考えることができます。
ここで述べられていることは、ちょうど図1に示したSMTシステムにおける矢印の向きを逆にしたものとなり、和文が生成される過程を示しています。これを生成モデルといい、これにおける翻訳の目的は、生成された和文から、最尤な英文を復元することになります。
2.2 統計
前項で述べたように、最適な翻訳結果とは、ある条件下における最尤な英文です。尤度を公式化するのに用いられる統計学上の基本的な記法を下記に挙げます。前述の通り、下記では和文をf、英文をeで示します。
合に、英文e(和文f)が形成される確率です。
- P(e)もしくはP(f) - 事前確率:英文eもしくは和文fが形成される確率です。
- P(e|f)もしくはP(f|e) - 条件付き確率:和文f(英文e)が既に形成されている場
- P(e, f) - 結合確率:英文eと和文fの両方が形成される確率です。
この定義により、P(e|f)はある和文から形成され得る全ての英文の確率分布をモデル化します。そのため、翻訳の問題は、下記の式で表される翻訳モデルを最大化するeを探すことであると公式化できます。
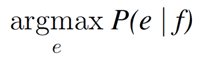
一方、項2.1で述べた生成モデルに基づくと、翻訳される和文fは、既に存在すると仮定する英文eに依存すると言えます。確率論および統計学においては、上記3種の確率分布の関係は、式2、もしくは式3で表すことができます。
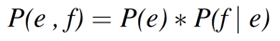
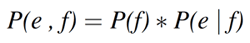
また、式2および式3より、ベイズの定理と呼ばれる下記の式が導かれます。
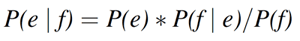
ベイズの定理は翻訳モデルP(e|f)と生成モデル P(e)*P(f|e) を結び付けます。したがって、最尤な翻訳結果を求める式1は、下記のように書き換えることができます。
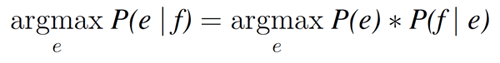
式5により、1)言語モデルの確率P(e)の推定、2)翻訳モデルの確率P(f|e)の推定、お
よび、3)その積を最尤化する最適なデコーディングアルゴリズムの考案、という、統計的機械翻訳における3つの課題が明らかになります。この記事では、最も広く用いられている言語モデル、およびにいくつかのスムージング法について説明していきます。




































