詳しい人求む！

数学の問題です。今、微分の問題をやってたのですが、よくわかりません。解説を見ても途中まではわかるの

締切済

質問者：高校生だにょ
質問日時：2025/01/23 14:10
回答数：5件

数学の問題です。
今、微分の問題をやってたのですが、よくわかりません。解説を見ても途中まではわかるのに、最後が何故そうなるのかわかりません。
教えて欲しいです。

解説のわからない所は別で貼ります

通報する

この質問への回答は締め切られました。

質問の本文を隠す

回答 (5件)

最新から表示
回答順に表示

No.5

回答者： takoハ
回答日時：2025/01/25 15:13

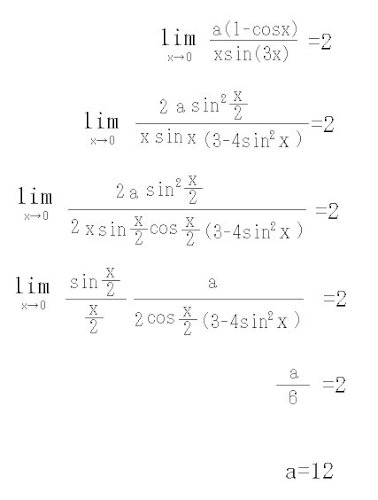
a(1-cosx)(1+cosx)/ xsin3x(1+cosx)=a sin^2 x / xsin3x (1+cosx)

=a x sin^2 x / x^2 sin3x (1+cosx)=a x /sin3x (1+cox)
=3x a / 3sin3x (1+cosx)
=a / 3(1+cosx)
→a / 3(1+1)=a /6
これが　2になるには　a/6=2 ∴a=2・6=12

lim x→0 sinx /x =0 を利用しいます

- 0
- 件

通報する

No.4

回答者： mtrajcp
回答日時：2025/01/25 05:23

t=x/2 とする

- 0
- 件

通報する

No.3

回答者： tknakamuri
回答日時：2025/01/23 16:42

1-cosx は cosxのテ―ラー展開から

(1/2)x^2-(1/24)x^4+・、・
xsin3xはsin3xのテーラー展開から
3x^2 - (1/6)(3^3)x^4+・・・

4次以降の項は極限では無視してよいので
lim[x→0]a(1-cosx)/(xsin3x)=a{(1/2)x^2}/(3x^2)=a/6=2
→a=12

- 1
- 件

通報する

No.2

回答者： mtrajcp
回答日時：2025/01/23 15:37

1-cosx=2{sin(x/2)}^2

sin(3x)=sinx{3-4(sinx)^2}
sinx=2sin(x/2)cos(x/2)

- 0
- 件

通報する

No.1

回答者：ありものがたり
回答日時：2025/01/23 15:23

lim a(1 - cos x)/(x sin 3x)

= lim a { (1 - cos x)/x^2 }{ x^2/sin 3x }
= a { lim (1 - cos x)/x^2 }{ lim x/sin 3x }
= a { 1/2 }{ 1/3 }
なので、
これが = 2 なら a = 12 です。

途中で使った計算は、
lim (1 - cos x)/x^2
= lim (1 - cos x)(1 + cos x)/{ x^2 (1 + cos x) }
= lim (1 - cos^2 x)/{ x^2 (1 + cos x) }
= lim { (sin x)/x }^2 ・ 1/(1 + cos x) }
= { lim (sin x)/x }^2 ・ { lim 1/(1 + cos x) }
= { 1 }^2 ・ { 1/(1 + 1) }
= 1/2,

lim x/sin 3x
= lim (1/3) 3x/sin 3x
= (1/3) lim 3x/sin3x
= (1/3) ・ 1
= 1/3.

lim[θ→0] (sinθ)/θ = 1 は
sin の定義に関わる基本公式でしたね。