自己組織化臨界現象(SOC)のページ
1999.8.17更新
SOC (Self-Organized Criticality; 自己組織化臨界現象)とは複雑性を生み出
すメカニズムです。
自然界の様々な現象は一見複雑に見えますが、ある簡単な規則に則っているよ
うに見えます。
それがSOCです。
あるサイズの現象の起こる頻度は、サイズが大きければ大きい程小さいという
ことで、さらに具体的にはlog(サイズ)-log(頻度)が比例関係になります。
SOCの例
・砂山(Sandpile)モデル
砂山に上から砂を加えて行くと時々砂山は崩れます。
この崩れのサイズとそのサイズの崩れの起こる頻度を両対数グラフにしてみる
と傾き一定の直線になります。
Per Bakのモデルはこれを数理モデル化したもので、コンピュータで簡単に計
算できます。
このモデルではL×Lに区切られた領域にランダムに粒子を加えて行きます。
粒子の数が4になったら、その場所の粒子は取り除き、前後左右の場所に1つず
つ粒子を加えます(領域外だったら粒子は捨ててしまいます)。
これを「雪崩」とよびます。
雪崩により隣の場所の粒子数が4になり、新たな雪崩が起こることもあります。
1つ外から粒子を加えたことによって系で起こる雪崩の回数と頻度の関係を見
てみるとこの雪崩現象がSOCであることが分かります。
実際に、Javaで作ったアプレットで見てみましょう。
下をクリックして下さい。
(このアプレットは重いです!!)
上の図は50×50の領域の粒子の数を表しています。
青色は0、水色は1、緑色は2、黄色は3、赤色は4です。
粒子の数が4(赤色)に達するとすぐに隣に分配されます(雪崩現象)。
4になった場所は赤枠で囲まれます。
シミュレーションはstartボタンをクリックすると開始し、stopボタンをクリックすると一時停止します(再開はstartボタン)。
下のグラフは雪崩の大きさ(横軸)とその頻度(縦軸)の関係のプロットです。
直線関係は見られるでしょうか?
(総雪崩回数が1000くらいに達しないと直線には見えません。
気長にお待ち下さい。
目測ですが、total=5000程度で傾きは-1.5程度になります)
・グーテンベルグ・リヒター則
地震のマグニチュードと頻度には簡単な関係が見られ、グーテンベルグ・リヒ
ター則と呼ばれています。
Mをマグニチュード、Nをそのマグニチュードの地震の起こる頻度とすると、
log N = a - b M
という関係が経験的に成り立ちます(bは0.7〜1.0程度)。
地震の発生機構などはまだ良く分かってなく、地震予知は今のところ不可能で
すが、どの程度の大きさの地震が何年に一度起こるかは大体予想することがで
きます。
グーテンベルグ・リヒター則によるとマグニチュードが1大きいと発生頻度は
およそ1/10になります。
また、地震のエネルギーEとマグニチュードMの間には
log E = 11.8 + 1.5 M
という関係があります。
したがって、地震のエネルギー(サイズ)と頻度との関係は
log N = a' - b' log E
となります。
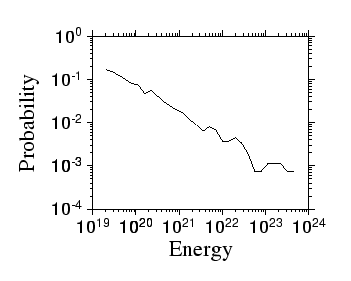
この関係をグラフにしました。
データは北緯25〜48°、東経125〜150°の範囲で、1961年から1985年の間に気
象庁が決めたM5以上の地震(理科年表より)です。
見事に直線関係が成り立っています。
岩瀬 康行 (
iwase@nda.ac.jp)
研究紹介のページへ

