[文章生成]PyTorchのRNNクラスを使って文章を生成してみよう:作って試そう! ディープラーニング工作室(1/2 ページ)
RNNを組み込んだニューラルネットワークを定義して、そこに分かち書きされたテキストから作成したデータを入力して学習を行い、文章がうまく生成されるかを見てみます。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
今回の目的
前回は、分かち書きされたテキストから辞書や学習に使用するデータセットを作成して、訓練データをPyTorchのEmbeddingクラスのインスタンスに入力→RNNクラスに順伝播→全結合層に順伝播→辞書の要素数の出力を得るまでの手順を見てみました。
今回は今述べた処理を行うニューラルネットワークモジュール(クラス)、学習を行う関数などを定義して、実際に学習を行い、最終的に梶井基次郎の小説データからどんな文章が生成されるかまでを見ていくことにします。
前回に記述したコードで、辞書を作成する関数やデータセットやデータローダーを定義するコードなど、今回も使用しているものは今回のノートブックには冒頭に記述してあります(それらのコードを実行するには分かち書きされたテキストファイルwakati.txtが必要です。その作成方法は前回のノートブックの末尾に掲載しているので、そちらを参照してください)。
なお、前回はPyTorchのEmbeddingクラスなどの動作を確認する目的でデータセットから読み込むデータ数(バッチサイズ)を2としていましたが、今回はバッチサイズを25としています。ここではそれらについての説明は省略します。実際のコードはノートブックをご覧ください。
ニューラルネットワークモジュールの定義
以下に「入力されたデータから次に生成する語を推測するニューラルネットワークモジュール」の定義を示します。
class Net(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_size,
batch_size=25, num_layers=1):
super().__init__()
self.hidden_size = hidden_size
self.batch_size = batch_size
self.num_layers = num_layers
self.device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0)
self.rnn = nn.RNN(embedding_dim, hidden_size,
batch_first=True, num_layers=self.num_layers)
self.fc = nn.Linear(hidden_size, vocab_size)
self = self.to(self.device)
def init_hidden(self, batch_size=None):
if not batch_size:
batch_size = self.batch_size
self.hidden_state = torch.zeros(self.num_layers, batch_size,
self.hidden_size).to(self.device)
def forward(self, x):
x = self.embedding(x)
x, self.hidden_state = self.rnn(x, self.hidden_state)
x = self.fc(x)
return x
__init__メソッドは(self以外に)以下の5つのパラメーターを取ります。
- vocab_size:辞書の要素数(実際にはパディング用のインデックス0を考慮して、実際の語彙+1を足したものを渡す)
- embedding_dim:Embeddingクラスのインスタンスで使用する埋め込みベクトルの次元数
- hidde_size:RNNクラスのインスタンスで使用する隠し状態のサイズ
- batch_size:RNNクラスのインスタンスに入力されるデータの数(バッチサイズ)
- num_layers:RNNのレイヤー数
これらのパラメーター(および、インスタンス変数self.deviceに設定しているCPUを使うかGPUを使うかの情報)を使用して、__init__メソッドでは前回にも見たように、Embedding/RNN/Linerクラスのインスタンスを生成しています。
一つだけ注意点があるとすると、RNNクラスのインスタンス生成時に「batch_first=True」を指定している点です。これについて少し説明をしておきましょう。
前回のEmbeddingクラスの動作確認するコードは次のようになっていました。
VS = len(w2i) + 1 # vocabulary size
ED = 5 # embedding dimension
embedding = nn.Embedding(VS, ED, padding_idx=0)
x = embedding(X_train)
# …… 省略 ……
print('x.shape:', x.shape)
# …… 省略 ……
この出力結果は「x.shape: torch.Size([2, 19, 5])」のようなものです。つまり、「バッチサイズ×インデックス列のサイズ×埋め込みベクトルの次元数」のデータが得られます。この場合は、19個の形態素(行)を5次元の埋め込みベクトル(列)で表現した行列がバッチサイズの数(2個)だけ並んだデータ(3階のテンソル)が、Embeddingクラスのインスタンスからの出力ということです。よって、これを受け取るRNNクラスのインスタンスを生成する際には「batch_first=True」として、今述べたような形状のデータが入力されることを教えるようにしています。
init__hiddenメソッドは隠し状態の初期化を行うためのものです。前回は以下のようなコードを使って、RNNクラスのインスタンスに隠し状態の初期値を渡していました。
rnn = nn.RNN(……)
h = torch.zeros(NM, BS, HS) # 隠し状態の初期化
r, h = rnn(x, h) # RNNにデータセットから得た値と隠し状態を渡す
この代わりに、ここではinit__hiddenメソッドを呼び出すようにしています。このメソッドはバッチサイズを指定できるようになっていますが、これは学習後のニューラルネットワークに文章生成をさせる際にバッチサイズを指定できるようにするためです。
最後のforwardメソッドではEmbedding/RNN/Linerクラスのインスタンスを順次呼び出すだけです。
ここでは次のような値を用いて、このNetクラスのインスタンスを生成することにしました(バッチサイズは冒頭で紹介したコードにあるデータローダーを定義する部分で「BATCH_SIZE = 25」として定義しています)。これらの値は筆者が適当に設定したものなので深い意味はありませんが(もっとよい値があるかもしれません)、まあこの値でやってみましょう。
EMBEDDING_DIM = 300
HIDDEN_SIZE = 300
NUM_LAYERS = 1
VOCAB_SIZE = len(w2i) + 1
Netクラスのインスタンス生成では上で定義した値を使うだけです。損失関数と最適化アルゴリズムの選択についてはこれまでに見てきたものを使うことにしました。
model = Net(VOCAB_SIZE, EMBEDDING_DIM, HIDDEN_SIZE, BATCH_SIZE, NUM_LAYERS)
criterion = nn.CrossEntropyLoss(ignore_index=0)
optimizer = torch.optim.SGD(model.parameters(), lr=0.03)
学習
学習を行うコードはtrain関数にまとめました。
def train(model, dataloader, criterion, optimizer, epochs, vocab_size):
device = model.device
model.train()
losses = []
for epoch in range(EPOCHS):
running_loss = 0
for cnt, (X_train, y_train) in enumerate(dataloader):
optimizer.zero_grad()
X_train, y_train = X_train.to(device), y_train.to(device)
model.init_hidden()
outputs = model(X_train)
outputs = outputs.reshape(-1, vocab_size)
y_train = y_train.reshape(-1)
loss = criterion(outputs, y_train)
running_loss += loss.item()
loss.backward()
optimizer.step()
losses.append(running_loss / cnt)
print('+', end='')
if epoch % 50 == 0:
print(f'\nepoch: {epoch:3}, loss: {loss:.3f}')
print(f'\nepoch: {epoch:3}, loss: {loss:.3f}')
return losses
これについては、これまでと同様の内容です。ニューラルネットワークモデルからの出力やその正解ラベルの形状を変形してから損失関数に渡している点には注意してください。
ここではエポック数を1000として学習を行います。
EPOCHS = 1000
losses = train(model, dataloader, criterion, optimizer, EPOCHS, VOCAB_SIZE)
これを実行すると、次のような結果になります。
この学習では最終的な損失は0.232となっています。まあまあよいところまで学習できたと考えられるかもしれません(実は損失以外にも重要な要素を本来はtrain関数の中で計算しておくべきなのですが、これについては次回以降に取り上げます)。
train関数の戻り値は学習時の損失の変化なので、これをプロットしましょう。
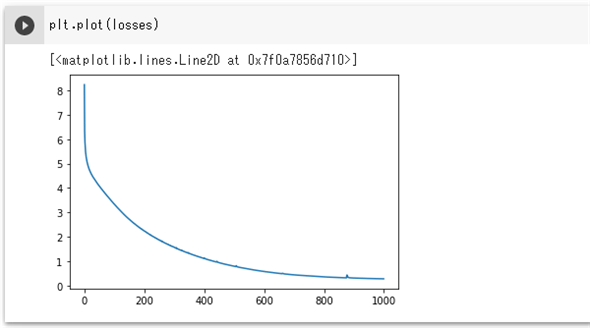
plt.plot(losses)
実行結果は次の通りです。
グラフを見ると、まだまだ損失は低くなりそうですが、それでも十分に学習できているように思えます。
Copyright© Digital Advantage Corp. All Rights Reserved.