Úhel

Úhel (přesněji rovinný úhel) může být definován jako:

• (jakožto rovinný útvar) část roviny, která je ohraničena dvěma polopřímkami se společným počátkem,
• (jakožto obecná geometrická struktura v rovině nebo v prostoru) dvojice polopřímek se společným počátkem nebo dvojice přímek se společným bodem,
• (ve smyslu orientovaný úhel) uspořádaná dvojice dvou orientovaných přímek se společným bodem nebo dvou polopřímek se společným počátkem nebo veličina charakterizující polohový vztah mezi nimi.

Zeleně vyznačený úhel tvoří dvě červené polopřímky vycházející ze stejného bodu (tzv. ramena úhlu), jenž tvoří vrchol úhlu. Obrázek je v kartézské soustavě souřadnic.

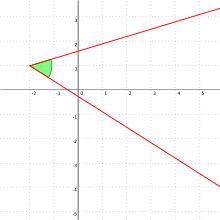
V prostoru se kromě rovinného úhlu definuje prostorový úhel (jako útvar a jemu odpovídající veličina).

Základní pojmy

• Polopřímky, které vymezují úhel v rovině, se nazývají ramena úhlu, společný počáteční bod polopřímek se nazývá vrchol úhlu.

• Do úhlu zahrnujeme i body ležící na polopřímkách ramen úhlu.

• Množina všech bodů úhlu, které neleží na žádné z polopřímek, se nazývá vnitřek úhlu. Množina všech bodů roviny, které nepatří do úhlu, se nazývá vnějšek úhlu.

Úhel se znázorňuje pomocí jeho ramen, mezi kterými se vyznačí oblouček kolem vrcholu úhlu. Zápis úhlu se provádí pomocí řeckého písmene, např. $\alpha$ (alfa), nebo pomocí symbolu úhlu a tří bodů v pořadí: pomocný bod na prvním rameně – vrchol – pomocný bod na druhém rameně, např. $\angle AVB$ (vrchol úhlu leží na středním bodu).

Druhy úhlů

Název úhlu		Popis	Podmínky
konvexní		konvexní úhel je konvexní obrazec; velikost takového úhlu je menší nebo rovna 180° (${\textstyle \pi \,rad}$) nebo rovna 360° (${\textstyle 2\pi \,rad}$)	α ≤ 180°
	nulový	úhel tvořený dvěma rameny, která jsou shodná a leží tedy na sobě (splývají v jednu polopřímku); jeho velikost je rovna 0° (${\textstyle 0\,rad}$) a má nulovou plochu (jde jen o jednorozměrný objekt)	α = 0°
	ostrý	úhel menší než pravý úhel; jeho velikost je větší než 0° (${\textstyle 0\,rad}$), ale menší než 90° (${\textstyle {\frac {\pi }{2}}\,rad}$)	0° < α < 90°
	pravý úhel	je polovina přímého úhlu (označujeme ho tečkou v obloučku). Dvě přímky v pravém úhlu (tedy vzájemně kolmé) dělí plochu na 4 shodné kvadranty; jeho velikost je 90° (${\textstyle {\frac {\pi }{2}}\,rad}$)	α = 90°
	tupý	úhel větší než pravý úhel, ale menší než přímý úhel; jeho velikost je větší než 90° (${\textstyle {\frac {\pi }{2}}\,rad}$), ale menší než 180° (${\textstyle \pi \,rad}$)	90° < α < 180°
	vypuklý	úhel, který je menší než přímý úhel; jeho velikost je menší než 180° (${\textstyle \pi \,rad}$)	α < 180°
kosý		společný název pro ostrý, pravý a tupý úhel; jeho velikost je větší než 0° a menší než 180° (${\textstyle \pi \,rad}$)	0° < α < 180°
přímý		úhel, jehož ramena jsou opačné polopřímky; jeho velikost je 180° (${\textstyle \pi \,rad}$); de facto se tak jedná o přímku, resp. polorovinu.	α = 180°
konkávní (dutý)		úhel, který je větší než přímý úhel, ale menší než plný úhel; úhel, který není konvexní; jeho velikost je větší než 180° (${\textstyle \pi \,rad}$), ale menší než 360° (${\textstyle 2\pi \,rad}$)	180° < α < 360°
plný		úhel, jehož ramena leží na sobě (splývají v jednu polopřímku), svou plochou obsahuje celou rovinu; jeho velikost je rovna 360° (${\textstyle 2\pi \,rad}$)	α = 360°

Označení používané v trigonometrii

• výškový úhel – úhel, který svírá směr, kterým pozorujeme předmět ve výšce s vodorovnou rovinou
• hloubkový úhel – úhel, který svírá směr, kterým pozorujeme předmět v hloubce s vodorovnou rovinou
• zorný úhel – úhel, který spolu svírají směry, kterými pozorujeme dvě nejodlehlejší místa předmětu (nebo také úhel pod kterým vidíme předmět)

Dvojice úhlů

V matematice jsou zvláštní dvojice úhlů pojmenované jako: vrcholové, vedlejší, souhlasné a střídavé.

• Vrcholové úhly – dva úhly, jejichž ramena jsou opačné polopřímky. Vrcholové úhly jsou shodné. Vrcholové úhly mají společný vrchol.

• Vedlejší úhly – dva úhly, jejichž jedno rameno je společné a druhá ramena jsou opačné polopřímky. Součet vedlejších úhlů je přímý úhel.

• Souhlasné úhly – dva úhly, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je stejný (souhlasný). Souhlasné úhly jsou shodné.

• Střídavé úhly – dva úhly, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je opačný (střídavý). Střídavé úhly jsou shodné.

Úhly příslušné k oblouku kružnice

• Středový úhel – úhel, jehož vrcholem je střed $S$, kružnice $k$ a ramena procházejí krajními body oblouku $AB$ kružnice $k$ ($\alpha$, $\beta$ – středové úhly).

• Obvodový úhel – každý úhel, jehož vrchol $V$ leží na kružnici $k$ a ramena procházejí krajními body oblouku $AB$ kružnice $k$ ($V\neq A$, $V\neq B$).

• Úsekový úhel – úhel, jenž svírá tětiva $AB$ kružnice $AB$ s tečnou $t$ kružnice $k$ v bodě $A$ (popř. bodě $B$).

Vztahy mezi velikostmi těchto úhlů popisuje následující obrázek:

Související informace naleznete také v článku Věta o obvodovém a středovém úhlu.

Souměrnost

Všechny úhly jsou osově souměrné, osa úhlu prochází vrcholem a rozděluje úhel na dvě shodné části (poloviny úhlu).

Orientovaný úhel

Orientovaným úhlem se nazývá uspořádaná dvojice polopřímek ${\overrightarrow {VA}}$, ${\overrightarrow {VB}}$ se společným bodem $V$, přičemž polopřímka ${\overrightarrow {VA}}$ se nazvývá počáteční rameno úhlu a polopřímka ${\overrightarrow {VB}}$ koncové rameno úhlu. Bod $V$ je vrcholem orientovaného úhlu.

Velikost úhlu

Velikost úhlu je nezáporné číslo, které lze přiřadit každému úhlu. Platí přitom, že shodné úhly mají stejnou velikost a také, že součet velikostí úhlů $\angle AVX$ a $\angle XVB$ je roven velikosti úhlu $\angle AVB$.

Číselná velikost úhlu je dána volbou nenulového úhlu, kterému přiřadíme velikost 1. V matematice i praxi se pro měření úhlu používá (viz níže): oblouková míra, stupňová míra, setinná míra, ale také například hodinová pozice pro vyjádření azimutu.

Oblouková (radiánová) míra

Hodnota jednotkového úhlu v obloukové míře je zvolena tak, že úhel o velikosti 1 vymezuje na kružnici se středem ve vrcholu úhlu oblouk, jehož délka je rovna poloměru dané kružnice. Hodnotu obloukové míry úhlu $\alpha$ značíme $\operatorname {arc} \alpha$.

Velikost libovolného úhlu je možné určit jako poměr délky oblouku vymezeného rameny na kružnici opsané kolem vrcholu k poloměru této kružnice, tzn.

$\alpha ={\frac {s}{r}}$,

kde $s$ je délka kruhového oblouku mezi přímkami, které vymezují úhel, a $r$ je poloměr kruhového oblouku. Velikost pravého úhlu je v obloukové míře rovna ${\frac {\pi }{2}}$.

Úhlová jednotka obloukové míry je radiánech (zkratka rad).

Stupňová míra

Stupňová míra (devadesátinná, nonagesimální) je zavedena tak, že pravý úhel je rozdělen na 90 dílů, které se nazývají (úhlové) stupně. Vztah mezi stupňovou a obloukovou mírou lze tedy zapsat jako

$1^{\circ }={\frac {\pi }{180}}\,\mathrm {rad}$

Vyjádření úhlu v šedesátkové soustavě: Úhlový stupeň se dělí na 60 (úhlových) minut, tzn. 1° = 60′. Pro úhlové minuty se používá také označení arcminute nebo arcmin. 60 arcmin = 60′ = 1°.
Každá úhlová minuta se dále dělí na 60 (úhlových) vteřin, tzn. 1′ = 60′′. Pro úhlové vteřiny se používá také označení arcsecond nebo arcsec. 3600 arcsec = 3600′′ = 60′ = 1°.

Vyjádření úhlu v desítkové soustavě: úhlový stupeň se dělí dekadicky, např. 22° 29′ 36′′ = 22,4933°.

Setinná míra

Setinná míra je zavedena tak, že pravý úhel je rozdělen na 100 dílů, které nazýváme gony (grady, setinné stupně). Vztah mezi setinnou a obloukovou mírou lze zapsat jako

$1^{\mathrm {g} }={\frac {\pi }{200}}\mathrm {rad}$

Setinný stupeň se dělí na 100 setinných minut, tzn. $1^{\mathrm {g} }=100^{\mathrm {c} }$, a každá setinná minuta se dělí na 100 setinných vteřin, tzn. $1^{\mathrm {c} }=100^{\mathrm {cc} }$.

Příklady

Jeden stupeň je 1/180 přímého úhlu, neboli přímý úhel má velikost 180°. Zlomky stupňů se vyjadřují buď v desítkové nebo v šedesátkové soustavě, viz následující příklady:

• půl stupně = 0,5° = 0° 30’ tj. 30 úhlových minut
• osmina stupně = 0,125° = 0° 7’ 30" tj. 7 úhlových minut a 30 vteřin.

Jeden radián je $1/\pi$ přímého úhlu.

Stupně se používají především z historických důvodů a také pro relativně snadné provádění jednoduchých výpočtů. Radiány mají výhodu při složitějších výpočtech – zvláště při derivování či integraci není třeba počítat se speciálními konstantami. Radián je navíc relativně intuitivní jednotka. Vyjadřuje přímo délku oblouku, vytyčeného daným úhlem na jednotkové kružnici.

Velikost orientovaného úhlu

Velikost orientovaného úhlu je (v obloukové míře) rovna $\alpha +k2\pi$, kde $\alpha$ je velikost stejného neorientovaného úhlu a $k$ je celé číslo. Velikost orientovaného úhlu je úhel, kterým musí projít počáteční rameno při otočení do koncového ramene. Člen $k2\pi$ představuje počet celých otoček kolem vrcholu úhlu.

Základní úhel

Základní úhel (resp. základní velikost orientovaného úhlu) je neorientovaná velikost úhlu, která spadá do zleva uzavřeného intervalu $\langle 0^{\circ },360^{\circ })$ nebo v obloukové míře $\langle 0,2\pi )$. Při převodu velikosti úhlu na základní úhel ve stupních proto opakovaně odečítáme/přičítáme 360°, dokud není výsledek v požadovaném intervalu. Velikost 0° se neupravuje a naopak velikost 360° je 0°. Velikost 400° převedeme na 40° (protože 400 − 360 = 40), velikost 800° je pak 80° (800 − 360 − 360 = 80°), velikost −60° převedeme na 300° (protože −60 + 360 = 300).

Rovinný úhel jako fyzikální veličina

Pravidlo pravé ruky

Rovinný úhel je také fyzikální veličina užívaná k udávání polohy v prostoru (sférické souřadnice, cylindrické souřadnice) a k popisu otáčivých pohybů a jejich skládání (včetně otáčení s různoběžnými osami). Nejedná se tedy pouze o rovinné, ale i ryze prostorové problémy.

V soustavě SI je hlavní jednotkou rovinného úhlu jakožto fyzikální veličiny 1 radián, normy připouštějí i jednotky (úhlový) stupeň, (úhlová) minuta a (úhlová) vteřina (dříve tzv. vedlejší jednotky, dnes mimosoustavové jednotky přípustné k použití se SI).

Pro vyjádření polohy roviny úhlu v prostoru a současně jeho orientace se původně skalární veličina zobecňuje na axiální vektor. Jeho směr leží v přímce kolmé k rovině úhlu procházející vrcholem úhlu. Orientace je konvencí stanovena tak, že při kolmém pohledu na rovinu úhlu s kladnou orientací (proti směru hodinových ručiček) směřuje vektor úhlu k pozorovateli. Jednoduše lze stanovit pravidlem pravé ruky: Položíme-li dlaň pravé ruky malíčkovým hřbetem na rovinu úhlu tak, že zahnuté články prstů směřují ve směru od počátečního ke koncovému rameni (v kinematice je to směr otáčení), ukazuje palec směr vektoru úhlu.

Toto prostorové zobecnění je oprávněné (neuvažujeme-li triviální případ úhlů v jedné rovině) pouze v případě velmi malých otočení; vektorová algebra platí pouze pro elementární (ve smyslu infinitezimální) úhly. Lze pak bez problémů používat i pro veličiny vzniklé časovou derivací úhlu: S využitím vektorového vyjádření úhlu ${\boldsymbol {\varphi }}$ pak lze jednoduše vektorově definovat i úhlovou rychlost ${\boldsymbol {\omega }}={\frac {\mathrm {d} {\boldsymbol {\varphi }}}{\mathrm {d} t}}$ a mnohé jiné veličiny.

Naopak pro obecné úhly je nutno volit jiný algebraický popis, aby byl konzistentní i pro skládání úhlů. Takové skládání totiž obecně není komutativní (tedy záleží na pořadí skládaných úhlů otočení) a znázornění úhlu axiálním vektorem je proto nekorektní. Pro analytický popis jsou například vhodné kvaterniony rotace, v nichž vystupují čtveřice Eulerových parametrů (zpravidla značených A, B, C, D), nebo parametrické vyjádření lineárně lomenou transformací se čtveřicí Cayleyových-Kleinových parametrů (zpravidla α, β, γ, δ).

Operace s úhly

Sčítání úhlů

Dva úhly se sečtou tak, že vezmete kružítko a libovolně přejedete úhel který máte narýsován, kružítko zapíchnete na libovolné místo na dolní čáře a jedete čarou k čáře 2. Dole na úhlu od čáry kružítka zapíchnete kružítko do dolní čáry do místa, kde se protínají čáry úhlu a kružítka a druhý konec kružítka na druhou čáru, kde se protíná čára úhlu a kružítka a necháte v kružítku velikost, kterou jste si z úhlu vytáhli. Máte-li 2 úhly na sečtení nechte si ještě pořád velikost kružítka z úhlu prvního a na druhém libovolně zapíchněte kružítko s velikostí z minulého úhlu na čáru druhého úhlu a táhněte s ním na druhou čáru a velikost na kružítku si opět nechte. Narýsujte čáru s jedním bodem a kružítko s pořád stejnou velikostí zapíchněte do bodu (bod musí být na levé straně) a táhněte s kružítkem doleva. Na obou úhlech zanikly ramena. Tam, kde se protíná kružítko a úhel, zapíchněte kružítko a jeďte do druhého ramena. Nechte si velikost a zapíchněte kružítko na narýsovanou čáru a na bodě zapíchněte a jeďte do minulé čáry od kružítka, než se střetnou, a pak pravítkem narýsujte čáru do bodu a to samé s druhým úhlem a na obrázku vidíte výsledek.

Odčítání úhlů. Dva úhly se odečtou tak, že se jedním ramenem přiloží dovnitř sebe a výsledný úhel vznikne mezi druhými dvěma rameny. Početně stačí odečíst velikosti úhlů.

Násobení úhlů přirozeným číslem. Násobení úhlu přirozeným číslem se převádí na opakované sčítání téhož úhlu tolikrát, kolik je dané přirozené číslo. Početně se vynásobí velikost úhlu daným přirozeným číslem.

Dělení úhlů dvěma. Úhel se dělí dvěma sestrojením osy úhlu. Početně se vydělí velikost úhlu dvěma. Konstrukčně nelze provést přesné dělení obecného úhlu třemi, úloha je známa pod jménem trisekce úhlu.

Operace s orientovanými úhly

Při operacích s orientovanými úhly je nutné zohlednit jejich znaménka.

Jestliže tedy k orientovanému úhlu $\alpha$ přičítáme orientovaný úhel $\beta$, který však je opačně orientován, je výsledek stejný jako bychom od neorientovaného úhlu o stejné velikosti jako má úhel $\alpha$ odčítali neorientovaný úhel o stejné velikosti jako má úhel $\beta$. Výsledkem takové operace je opět orientovaný úhel, který má stejnou orientaci jako $\alpha$, jestliže $\alpha >\beta$, nebo má orientaci jako úhel $\beta$, jestliže $\alpha <\beta$.

Operace s úhly jakožto vektorovými veličinami

Skládání (vektorový součet)

Lze-li koncové rameno jednoho rovinného úhlu v prostoru ztotožnit s počátečním ramenem druhého úhlu stejného axiálního směru (stejné roviny úhlu), je úhel mezi počátečním ramenem prvního úhlu a koncovým ramenem druhého úhlu dán jejich vektorovým součtem. Takto lze skládat otočení v prostoru kolem stejné osy. Pro elementární (ve smyslu infinitezimální) úhly otočení kolem společného bodu platí vektorové skládání i pro obecné směry obou vektorů (roviny úhlů resp. osy otočení mohou být různé).

Násobení skalární veličinou

Velikost a rozměr výsledku je dán součinem velikostí a rozměrů (v soustavě SI a většině dalších soustav jednotek je úhel bezrozměrná veličina, má tedy rozměr 1), směr se nemění (je-li velikost záporná, znamená to opačnou orientaci ve stejné směrové přímce).

Skalární a vektorový součin s jinými vektorovými veličinami

S vektorově chápaným elementárním rovinným úhlem lze zacházet jako s jinými axiálními vektory. Proto rozměr součinu je součinem rozměrů a výsledkem jejich

• skalárního součinu
  • s pravým vektorem je pseudoskalár,
  • s axiálním vektorem je skalár,
  • obojí s velikostí danou součinem velikostí násobeným kosinem úhlu sevřeným oběma vektory;
• vektorového součinu
  • s pravým vektorem je axiální vektor,
  • s axiálním vektorem je pravý vektor,
  • obojí s velikostí danou součinem velikostí násobeným sinem úhlu sevřeným oběma vektory.

Měřicí přístroje

Měření úhlů je v praxi velmi důležité. Využívá je astronomie, geodézie a mnoho dalších oborů. Proto se také vyvinula řada měřicích přístrojů. Úhloměr je i základem mnoha druhů dálkoměrů.

• Úhloměr – nejjednodušší měřidlo – jedná se o polokruhovou desku se stupnicí po obvodu. Složitější přístroje mají pohyblivé rameno.
• Jakubova hůl – jednoduchý středověký astronomický přístroj měřící na principu porovnávání stran trojúhelníku.
• Kvadrant, sextant, oktant – používané v navigaci.

Související články

• Trisekce úhlu
• Prostorový úhel
• Hodinová pozice
• Azimut

Externí odkazy

• Slovníkové heslo úhel ve Wikislovníku
• Obrázky, zvuky či videa k tématu úhel na Wikimedia Commons

Autoritní data	BNF: cb14519948f (data) GND: 4189964-7 LCCN: sh85005042 NLI: 987007294852305171

Portály: Matematika