Arukone


Arukone (japanisch アルコネ) bzw. Nanbarinku (japanisch ナンバーリンク) ist ein japanisches Logikrätsel, das erstmals von der japanischen Zeitschrift Nikoli veröffentlicht wurde.
Arukone ist auch unter anderen Namen bekannt, dazu gehören: Number Link, Alphabet Connection, ABC Connection und Buchstabenbund.
Regeln
[Bearbeiten | Quelltext bearbeiten]Arukone wird auf einem rechteckigen Quadratgitter von beliebiger Größe gespielt. Auf einigen Feldern sind Buchstaben vorgegeben. Ziel des Spieles ist es, alle Felder mit Buchstaben so miteinander zu verbinden, dass folgende Regeln gelten:
- Alle Felder mit gleichen Buchstaben müssen miteinander durch eine einzige, durchgehende Linie verbunden sein.
- An jedem Feld mit einem Buchstaben beginnt oder endet nur genau eine Linie.
- Die einzelnen Abschnitte eines Linienzugs verlaufen entweder horizontal oder vertikal.
- Jedes Feld darf nur einen Teil eines einzigen Linienzug enthalten und insbesondere dürfen Linienzüge sich nicht kreuzen.
Zudem ist es üblich Buchstaben in alphabetischer Reihenfolge vorzugeben. Manchmal sind auch Zahlen statt Buchstaben verwendet. Die Regeln lauten dann entsprechend.
Normalerweise wird die Lösung durch die vorgegebenen Buchstaben oder Zahlen eindeutig festgelegt.
Varianten
[Bearbeiten | Quelltext bearbeiten]Manchmal wird zu den obigen Regeln noch die Regel hinzugenommen, dass jedes Feld genau einen Teil eines Linienzuges enthalten muss, dass also kein Feld in einer Lösung frei bleiben darf.
Lösungsstrategien
[Bearbeiten | Quelltext bearbeiten]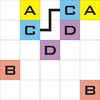
Zur Lösung einer Arukone versucht man normalerweise nach und nach einzelne Buchstaben miteinander zu verbinden, die sich dann zur gesuchten Lösung ergeben.
So gibt es manchmal (wie auch im Beispiel links) für die Verbindung zweier Buchstaben überhaupt nur genau einen Weg, der dann auch so verlaufen muss. Andere Linienzüge zwischen zwei gleichen Buchstaben lassen sich dadurch ausschließen, dass es dann überhaupt keinen Linienzug mehr für ein anderes Buchstabenpaar gibt.
Durch logische Überlegungen lassen sich eine Vielzahl von weiteren Lösungsstrategien angeben, die letztendlich zur gesuchten Lösung führen.