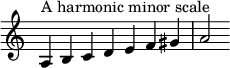Wikipedia

Harmonic minor scale

(Redirected from Harmonic minor)

The harmonic minor scale (or Aeolian ♮7 scale) is a musical scale derived from the natural minor scale, with the minor seventh degree raised by one semitone to a major seventh,[2][3][4] creating an augmented second between the sixth and seventh degrees.

\relative c { \clef bass \time 2/2 \key g \minor \tempo "Allegro" g2 a bes4 c2 d4 es2 fis g1 }
Theme in harmonic minor from the opening of Schumann's First Symphony (1841)[1]
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 a4^\markup { A harmonic minor scale } b c d e f gis a2 } }

Thus, a harmonic minor scale is represented by the following notation:

1, 2, ♭3, 4, 5, ♭6, 7, 8

A harmonic minor scale can be built by lowering the 3rd and 6th degrees of the parallel major scale by one semitone.

Because of this construction, the 7th degree of the harmonic minor scale functions as a leading tone to the tonic because it is a semitone lower than the tonic, rather than a whole tone lower than the tonic as it is in natural minor scales. The intervals between the notes of a harmonic minor scale follow the sequence below:

whole, half, whole, whole, half, augmented second, half

While it evolved primarily as a basis for chords,[5] the harmonic minor with its augmented second is sometimes used melodically. Instances can be found in Mozart, Beethoven (for example, the finale of his String Quartet No. 14), and Schubert (for example, in the first movement of the Death and the Maiden Quartet). In this role, it is used while descending far more often than while ascending. A familiar example of the descending scale is heard in a Ring of bells. A ring of twelve is sometimes augmented with a 5♯ and 6♭ to make a 10 note harmonic minor scale from bell 2 to bell 11 (for example, Worcester Cathedral).[6]

In popular music, examples of songs in harmonic minor include Katy B's "Easy Please Me", Bobby Brown's "My Prerogative", and Jazmine Sullivan's "Bust Your Windows". The scale also had a notable influence on heavy metal, spawning a sub-genre known as neoclassical metal, with guitarists such as Chuck Schuldiner, Yngwie Malmsteen, Ritchie Blackmore, and Randy Rhoads employing it in their music.[7]

Harmony

edit

The scale is called the harmonic minor scale because it is a common foundation for harmonies (chords) in minor keys. Traditionally, "the main use for harmonic minor, when improvising or creating melodies, is over the V7 chord, not for use over the i chord."[8] For example, in the key of A minor, the dominant (V) chord (the triad built on the 5th scale degree, E) is a minor triad in the natural minor scale. But when the seventh degree is raised from G♮ to G♯, the triad becomes a major triad. "In fact, it created even more tension than the major key V7. This is because the scale not only outlines the notes of E7 [V7] but also adds new tension notes like the ♯5 [C to B] and ♭9 [F to E]."[8]

Chords on degrees other than V may also include the raised 7th degree, such as the diminished triad on VII itself (viio), which has a dominant function, as well as an augmented triad on III (III+), which is not found in any "natural" harmony (that is, harmony that is derived from harmonizing the seven western modes, which include "major" and "minor"). This augmented fifth chord (♯5 chord) played a part in the development of modern chromaticism.

The triads built on each scale degree follow a distinct pattern. The roman numeral analysis is shown below.

 

An interesting property of the harmonic minor scale is that it contains two chords that are each generated by just one interval:

  1. an augmented triad (III+), which is generated by major thirds
  2. a diminished seventh chord (viio7), which is generated by minor thirds

Because they are generated by just one interval, the inversions of augmented triads and diminished seventh chords introduce no new intervals (allowing for enharmonic equivalents) that are absent from its root position. That is, any inversion of an augmented triad (or diminished seventh chord) is enharmonically equivalent to a new augmented triad (or diminished seventh chord) in root position. For example, the triad E♭–G–B in first inversion is G–B–E♭, which is enharmonically equivalent to the augmented triad G–B–D♯. One chord, with various spellings, may therefore have various harmonic functions in various keys.

The seventh chords built on each scale degree follow a distinct pattern. The roman numeral analysis is shown in parentheses below.

Harmonic minor contains seven types of seventh chords: a minor major seventh chord (im(maj7)), a half-diminished seventh chord (iim7(−5)), an augmented major seventh chord (IIIaug(maj7)), a minor seventh chord (ivm7), a dominant seventh chord (V7), a major seventh chord (VImaj7), and a diminished seventh chord (viidim7). Natural minor only contains four types of seventh chords: three minor seventh chords (im7, ivm7, and vm7), a half-diminished seventh chord (iim7(-5)), two major seventh chords (IIImaj7 and VImaj7), and a dominant seventh chord (VII7).

 

Modes of harmonic minor scale

edit

Like Ionian (or major) scale, harmonic minor scale has seven modes, but since the character of harmonic minor is quite the same as Aeolian (natural minor), the modes from Ionian will be rearranged to be started from Aeolian.

Mode Name of scale Degrees Notes (on A) Triad chords Seventh chords
1 Harmonic minor (or Aeolian ♯7) 1 2 ♭3 4 5 ♭6 7 8 A B C D E F G♯ A Am Ammaj7 (9, 11, ♭13)
2 Locrian ♮6 1 ♭2 ♭3 4 ♭5 6 ♭7 8 A B♭ C D E♭ F♯ G A Aο or Am♭5 Aø7 (♭9, 11, 13)
3 Ionian ♯5 (or augmented major) 1 2 3 4 ♯5 6 7 8 A B C♯ D E♯ F♯ G♯ A A+ A+maj7 (9, 11, 13)
4 Ukrainian Dorian
Dorian #11 (or Dorian #4, Romanian minor), Arabic Nikriz, Mi Sheberakh,
(or altered dorian) 		1 2 ♭3 ♯4 5 6 ♭7 8 A B C D♯ E F♯ G A Am Am7 (9, ♯11, 13)
5 Phrygian dominant scale, Hijaz,Double Harmonic Majorb7,

Freygish

1 ♭2 3 4 5 ♭6 ♭7 8 A B♭ C♯ D E F G A A A7 (♭9, 11, ♭13)
6 Lydian ♯2 1 ♯2 3 ♯4 5 6 7 8 A B♯ C♯ D♯ E F♯ G♯ A A Amaj7 (♯9, ♯11, 13)
7 Super-Locrian scale  7
(or altered diminished) 		1 ♭2 ♭3 ♭4 ♭5 ♭6  7 8 A B♭ C D♭ E♭ F G♭ A Aο or Am♭5 Aο7 (♭9, ♭11, ♭13)

See also

edit

References

edit
  1. ^ Forte, Allen (1979). Tonal Harmony, p. 13. Third edition. Holt, Rinhart, and Winston. ISBN 0-03-020756-8.
  2. ^ McKinley, Carl (2011). Harmonic Relations, p.37. Wipf & Stock Publishers. ISBN 9781610975315.
  3. ^ Seeger, Charles (1916). Harmonic Structure and Elementary Composition: An Outline of a Course in Practical Musical Invention, p.13. C.L. Seeger & E.G. Stricklen. ISBN 9785871501719.
  4. ^ Mokrejs, John (1913). Lessons in Harmony, p.41. Odowan Publishing Company. [ISBN unspecified].
  5. ^ Willard A. Palmer, Morton Manus, Amanda Vick Lethco (1994). Scales, Chords, Arpeggios and Cadences: Complete Book, p.14. Alfred. ISBN 9780739003688. "To find the primary triads in a MINOR KEY, the HARMONIC MINOR SCALE is used."
  6. ^ "Dove's Guide", Dove's Guide for Church Bell Ringers.
  7. ^ "Neo-Classical Metal Music Genre Overview | AllMusic". AllMusic. Retrieved 2018-11-26.
  8. ^ a b Mock, Don (1998). Secrets: Harmonic Minor Revealed, p.5. Alfred Music. ISBN 9780769200293.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Harmonic_minor_scale&oldid=1240565756"