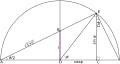Tangent half-angle substitution

In integral calculus, the Weierstrass substitution,, also known as the tangent half-angle substitution, universal trigonometric substitution, the half-tangent substitution, or the half-angle substitution, is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of ${\textstyle x}$ into an ordinary rational function of ${\textstyle t}$ by setting ${\textstyle t=\tan {\tfrac {x}{2}}}$. This is the one-dimensional stereographic projection of the circle onto the line. The general transformation formula is:

$$\int f(\sin x,\cos x)\,dx=\int f{\left({\frac {2t}{1+t^{2}}},{\frac {1-t^{2}}{1+t^{2}}}\right)}{\frac {2\,dt}{1+t^{2}}}.$$

History

The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to solve the integral ${\textstyle \int dx/(a+b\cos x)}$ in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. James Stewart named it after Karl Weierstrass when discussing the substitution in his popular 1987 calculus textbook. Michael Spivak wrote that this method was the "sneakiest substitution" in the world.

The substitution

Introducing a new variable ${\textstyle t=\tan {\tfrac {x}{2}},}$ sines and cosines can be expressed as rational functions of $t$, and $dx$ can be expressed as the product of $dt$ and a rational function of $t$, as follows: $$\sin x={\frac {2t}{1+t^{2}}},\qquad \cos x={\frac {1-t^{2}}{1+t^{2}}},\qquad {\text{and}}\qquad dx={\frac {2}{1+t^{2}}}\,dt.$$

Derivation of the formulas

Using the double-angle formulas, introducing denominators equal to one thanks to Pythagorean theorem, and then dividing numerators and denominators by ${\textstyle \cos ^{2}{\tfrac {x}{2}},}$ one gets

$${\begin{aligned}\sin x&={\frac {2\sin {\tfrac {x}{2}}\,\cos {\tfrac {x}{2}}}{\cos ^{2}{\tfrac {x}{2}}+\sin ^{2}{\tfrac {x}{2}}}}={\frac {2\tan {\tfrac {x}{2}}}{1+\tan ^{2}{\tfrac {x}{2}}}}={\frac {2t}{1+t^{2}}},\\[18mu]\cos x&={\frac {\cos ^{2}{\tfrac {x}{2}}-\sin ^{2}{\tfrac {x}{2}}}{\cos ^{2}{\tfrac {x}{2}}+\sin ^{2}{\tfrac {x}{2}}}}={\frac {1-\tan ^{2}{\tfrac {x}{2}}}{1+\tan ^{2}{\tfrac {x}{2}}}}={\frac {1-t^{2}}{1+t^{2}}}.\end{aligned}}$$

Finally, since ${\textstyle t=\tan {\tfrac {x}{2}}}$, the differentiation rules imply

$dt={\tfrac {1}{2}}\left(1+\tan ^{2}{\tfrac {x}{2}}\right)dx={\frac {1+t^{2}}{2}}dx,$

and thus

$dx={\frac {2}{1+t^{2}}}dt.$

Examples

First example: the cosecant integral

$${\begin{aligned}\int \csc x\,dx&=\int {\frac {dx}{\sin x}}\\[6pt]&=\int \left({\frac {1+t^{2}}{2t}}\right)\left({\frac {2}{1+t^{2}}}\right)dt&&t=\tan {\tfrac {x}{2}}\\[6pt]&=\int {\frac {dt}{t}}\\[6pt]&=\ln |t|+C\\[6pt]&=\ln \left|\tan {\tfrac {x}{2}}\right|+C.\end{aligned}}$$

We can confirm the above result using a standard method of evaluating the cosecant integral by multiplying the numerator and denominator by ${\textstyle \csc x-\cot x}$ and performing the substitution ${\textstyle u=\csc x-\cot x,}$ ${\textstyle du=\left(-\csc x\cot x+\csc ^{2}x\right)\,dx}$. $${\begin{aligned}\int \csc x\,dx&=\int {\frac {\csc x(\csc x-\cot x)}{\csc x-\cot x}}\,dx\\[6pt]&=\int {\frac {\left(\csc ^{2}x-\csc x\cot x\right)\,dx}{\csc x-\cot x}}\qquad u=\csc x-\cot x\\[6pt]&=\int {\frac {du}{u}}\\&=\ln |u|+C\\[6pt]&=\ln |\csc x-\cot x|+C.\end{aligned}}$$

These two answers are the same because ${\textstyle \csc x-\cot x=\tan {\tfrac {x}{2}}\colon }$

$${\begin{aligned}\csc x-\cot x&={\frac {1}{\sin x}}-{\frac {\cos x}{\sin x}}\\[6pt]&={\frac {1+t^{2}}{2t}}-{\frac {1-t^{2}}{1+t^{2}}}{\frac {1+t^{2}}{2t}}\qquad \qquad t=\tan {\tfrac {x}{2}}\\[6pt]&={\frac {2t^{2}}{2t}}=t\\[6pt]&=\tan {\tfrac {x}{2}}\end{aligned}}$$

The secant integral may be evaluated in a similar manner.

Second example: a definite integral

$${\begin{aligned}\int _{0}^{2\pi }{\frac {dx}{2+\cos x}}&=\int _{0}^{\pi }{\frac {dx}{2+\cos x}}+\int _{\pi }^{2\pi }{\frac {dx}{2+\cos x}}\\[6pt]&=\int _{0}^{\infty }{\frac {2\,dt}{3+t^{2}}}+\int _{-\infty }^{0}{\frac {2\,dt}{3+t^{2}}}&t&=\tan {\tfrac {x}{2}}\\[6pt]&=\int _{-\infty }^{\infty }{\frac {2\,dt}{3+t^{2}}}\\[6pt]&={\frac {2}{\sqrt {3}}}\int _{-\infty }^{\infty }{\frac {du}{1+u^{2}}}&t&=u{\sqrt {3}}\\[6pt]&={\frac {2\pi }{\sqrt {3}}}.\end{aligned}}$$

In the first line, one does not simply substitute ${\textstyle t=0}$ for both limits of integration. The singularity (in this case, a vertical asymptote) of ${\textstyle t=\tan {\tfrac {x}{2}}}$ at ${\textstyle x=\pi }$ must be taken into account. Alternatively, first evaluate the indefinite integral then apply the boundary values. $${\begin{aligned}\int {\frac {dx}{2+\cos x}}&=\int {\frac {1}{2+{\frac {1-t^{2}}{1+t^{2}}}}}{\frac {2\,dt}{t^{2}+1}}&&t=\tan {\tfrac {x}{2}}\\[6pt]&=\int {\frac {2\,dt}{2(t^{2}+1)+(1-t^{2})}}=\int {\frac {2\,dt}{t^{2}+3}}\\[6pt]&={\frac {2}{3}}\int {\frac {dt}{{\bigl (}t{\big /}{\sqrt {3}}{\bigr )}^{2}+1}}&&u=t{\big /}{\sqrt {3}}\\[6pt]&={\frac {2}{\sqrt {3}}}\int {\frac {du}{u^{2}+1}}&&\tan \theta =u\\[6pt]&={\frac {2}{\sqrt {3}}}\int \cos ^{2}\theta \sec ^{2}\theta \,d\theta ={\frac {2}{\sqrt {3}}}\int d\theta \\[6pt]&={\frac {2}{\sqrt {3}}}\theta +C={\frac {2}{\sqrt {3}}}\arctan \left({\frac {t}{\sqrt {3}}}\right)+C\\[6pt]&={\frac {2}{\sqrt {3}}}\arctan \left({\frac {\tan {\tfrac {x}{2}}}{\sqrt {3}}}\right)+C.\end{aligned}}$$ By symmetry, $${\begin{aligned}\int _{0}^{2\pi }{\frac {dx}{2+\cos x}}&=2\int _{0}^{\pi }{\frac {dx}{2+\cos x}}=\lim _{b\rightarrow \pi }{\frac {4}{\sqrt {3}}}\arctan \left({\frac {\tan {\tfrac {x}{2}}}{\sqrt {3}}}\right){\Biggl |}_{0}^{b}\\[6pt]&={\frac {4}{\sqrt {3}}}{\Biggl [}\lim _{b\rightarrow \pi }\arctan \left({\frac {\tan {\tfrac {b}{2}}}{\sqrt {3}}}\right)-\arctan(0){\Biggl ]}={\frac {4}{\sqrt {3}}}\left({\frac {\pi }{2}}-0\right)={\frac {2\pi }{\sqrt {3}}},\end{aligned}}$$ which is the same as the previous answer.

Third example: both sine and cosine

$${\begin{aligned}\int {\frac {dx}{a\cos x+b\sin x+c}}&=\int {\frac {2dt}{a(1-t^{2})+2bt+c(t^{2}+1)}}\\[6pt]&=\int {\frac {2dt}{(c-a)t^{2}+2bt+a+c}}\\[6pt]&={\frac {2}{\sqrt {c^{2}-(a^{2}+b^{2})}}}\arctan \left({\frac {(c-a)\tan {\tfrac {x}{2}}+b}{\sqrt {c^{2}-(a^{2}+b^{2})}}}\right)+C\end{aligned}}$$ if ${\textstyle c^{2}-(a^{2}+b^{2})>0.}$

Geometry

The tangent half-angle substitution parametrizes the unit circle centered at (0, 0). Instead of +∞ and −∞, we have only one ∞, at both ends of the real line. That is often appropriate when dealing with rational functions and with trigonometric functions. (This is the one-point compactification of the line.)

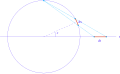
As x varies, the point (cos x, sin x) winds repeatedly around the unit circle centered at (0, 0). The point

$$\left({\frac {1-t^{2}}{1+t^{2}}},{\frac {2t}{1+t^{2}}}\right)$$

goes only once around the circle as t goes from −∞ to +∞, and never reaches the point (−1, 0), which is approached as a limit as t approaches ±∞. As t goes from −∞ to −1, the point determined by t goes through the part of the circle in the third quadrant, from (−1, 0) to (0, −1). As t goes from −1 to 0, the point follows the part of the circle in the fourth quadrant from (0, −1) to (1, 0). As t goes from 0 to 1, the point follows the part of the circle in the first quadrant from (1, 0) to (0, 1). Finally, as t goes from 1 to +∞, the point follows the part of the circle in the second quadrant from (0, 1) to (−1, 0).

Here is another geometric point of view. Draw the unit circle, and let P be the point (−1, 0). A line through P (except the vertical line) is determined by its slope. Furthermore, each of the lines (except the vertical line) intersects the unit circle in exactly two points, one of which is P. This determines a function from points on the unit circle to slopes. The trigonometric functions determine a function from angles to points on the unit circle, and by combining these two functions we have a function from angles to slopes.

Gallery

• 
  (1/2) The tangent half-angle substitution relates an angle to the slope of a line.
• 
  (2/2) The tangent half-angle substitution illustrated as stereographic projection of the circle.

Hyperbolic functions

As with other properties shared between the trigonometric functions and the hyperbolic functions, it is possible to use hyperbolic identities to construct a similar form of the substitution, ${\textstyle t=\tanh {\tfrac {x}{2}}}$:

$${\begin{aligned}&\sinh x={\frac {2t}{1-t^{2}}},\qquad \cosh x={\frac {1+t^{2}}{1-t^{2}}},\qquad \tanh x={\frac {2t}{1+t^{2}}},\\[6pt]&\coth x={\frac {1+t^{2}}{2t}},\qquad \operatorname {sech} x={\frac {1-t^{2}}{1+t^{2}}},\qquad \operatorname {csch} x={\frac {1-t^{2}}{2t}},\\[6pt]&{\text{and}}\qquad dx={\frac {2}{1-t^{2}}}\,dt.\end{aligned}}$$

Geometrically, this change of variables is a one-dimensional analog of the Poincaré disk projection.

See also

• Rational curve
• Stereographic projection
• Tangent half-angle formula
• Trigonometric substitution
• Euler substitution

Further reading

• Courant, Richard (1937) [1934]. "1.4.6. Integration of Some Other Classes of Functions §1–3". Differential and Integral Calculus. Vol. 1. Blackie & Son. pp. 234–237.

• Edwards, Joseph (1921). "§1.6.193". A Treatise on the Integral Calculus. Vol. 1. Macmillan. pp. 187–188.

• Hardy, Godfrey Harold (1905). "VI. Transcendental functions". The integration of functions of a single variable. Cambridge. pp. 42–51. Second edition 1916, pp. 52–62

• Hermite, Charles (1873). "Intégration des fonctions transcendentes" [Integration of transcendental functions]. Cours d'analyse de l'école polytechnique (in French). Vol. 1. Gauthier-Villars. pp. 320–380.

• Weierstrass, Karl (1915). "8. Bestimmung des Integrals ...". Mathematische Werke von Karl Weierstrass [Mathematical Works of Karl Weierstrass] (in German). Vol. 6. Mayer & Müller. pp. 89–99.

External links

• Weierstrass substitution formulas at PlanetMath