Parabolo (matematiko)

Parabolo estas koniko, kiun oni produktas per la intersekco de konuso kun ebeno paralela al tanĝanta ebeno de la konuso. Oni ankaŭ povas difini ĝin kiel la lokaro de punktoj, kiuj estas egaldistancaj de donita punkto (la fokuso) kaj donita linio (la direktanto).

Parabolo kaj aliaj konikoj

Saltanta pilko sekvas parabolajn kurbojn.

Konsideru direktanton L, kies ekvacio estas la linio x = −a, kaj fokuson F kun koordinatoj (a, 0). Se (x, y) estas punkto sur la parabolo tiam, pro la difino de parabolo, ĝiaj distancoj ĝis la direktanto kaj la fokuso egalas, matematike tio skribiĝas jene:

$|x+a|={\sqrt {(x-a)^{2}+y^{2}}}\,.$

Kvadradante la du termojn kaj simpligante, oni obtenas la jenan ekvacion:

$y^{2}=4ax\ ,$

kiuj estas la ekvacio de parabolo.

Interŝanĝante la rolojn de x kaj y oni obtenas la respondan ekvacion de parabolo kun vertikala akso tiele:

$x^{2}=4ay\$

La ekvacio ĝeneraliĝas al loko de la parabola ekstremo ekster la origino de la koordinataksoj per difino de ĝiaj koordinatoj (h, k). La ekvacio de parabolo kun vertikala akso iĝas:

$(x-h)^{2}=4a(y-k)\,.$

Oni povas skribi tiun lastan ekvacion tiele:

$y=\alpha x^{2}+\beta x+\gamma \,,$

t.e. la bildo de iu ajn funkcio priskribita per polinomo de grado 2 kun variablo x estas vertikalaksa parabolo.

Pli ĝenerale, en la karteziaj koordinatoj, la ekvacio de parabolo estas de la polinoma formo:

Ax² + Bxy + Cy² + Dx + Ey + F = 0 (kie minumume unu el A, B, C ne estas nulo),

kun la kondiĉo: B² - 4AC = 0 .

• 
  Parabola kurbo montranta direktanton (L) kaj fokuso (F); la distanco inter ĉiu punkto de la parabolo kaj la fokuso (PnF) egalas la ortan distancon de la sama punkto al la direktanton (PnQn).
• 
  Parabolo montrante, ke ĉiuj reflektaj radioj kiuj originis de infinito konverĝas al la fokuso.
• 
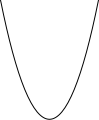
  Parabolo kun vertikala akso.
• 
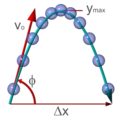
  Pri pafado, la distanco $\Delta x$ atingita de la kuglo post ĝia parabola trajektorio dependas de la komencaj rapido kaj angulo fare de la pafilo.

Vidu ankaŭ

• Kateno (kurboformo de pendantaj ĉenoj)