Politopo de cruce
En geometría, un politopo de cruce u ortoplex, es un politopo regular convexo que existe en cualquier número de dimensiones. Los vértices de un politopo de cruce consisten de todas las permutaciones de (±1, 0, 0, …, 0). El politopo de cruce es el casco o envoltorio convexo de sus vértices. (Nota: algunos autores definen al politopo convexo sólo como la envoltura de esta región).
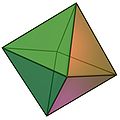
En una dimensión, el politopo de cruce es simplemente un segmento de línea [−1, +1], en dos dimensiones es el cuadrado con vértices {(±1, 0), (0, ±1)}. En tres dimensiones es el octaedro (uno de los cinco poliedros conocidos como sólidos platónicos. Los politopos de cruce en mayor número de dimensiones son generalizaciones de estos.

|
|
| ||
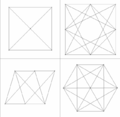
| 2 dimensiones | 3 dimensiones | 4 dimensiones |
El politopo de cruce es el dual del politopo de medida.
Cuatro dimensiones
editarEl politopo de cruce de cuatro dimensiones tiene el nombre de hexadecacoron o 16-cell, uno de los seis polícoros regulares. Estos polícoros fueron descriptos originalmente por el matemático suizo Ludwig Schläfli a mediados del siglo XIX.
Dimensiones mayores
editarEn n dimensiones con n > 4 existen sólo tres politopos regulares: el simplex, el politopo de medida, y el politopo de cruce, siendo estos dos últimos duales y el simplex auto-dual.
El politopo de cruce n-dimensional tiene 2n vértices, y 2n facetas (componentes (n−1)-dimensionales) todos los cuales son n−1-simplices. Las figuras de vértice son todas politopos de cruce (n−1)dimensionales. El símbolo de Schläfli del politopo de cruce es {3,3,…,3,4}.
El número de componentes k-dimensionales (vértices, aristas, caras, …, facetas) de un politopo de cruce n-dimensional está determinado por (ver coeficiente binomial):
Para los primeros n y k tendremos:
| n | βn k11 |
Name(s) Grafo |
Grafo 2n-gono |
Grafo 2(n-1)-gono |
Schläfli | Vértices | Aristas | Caras | 3-caras | 4-caras | 5-caras | 6-caras | 7-caras | 8-caras | 9-caras | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | β1 | Segmento 1-ortoplex |
{} | 2 | ||||||||||||
| 2 | β2 −111 |
Cuadrado 2-ortoplex Bicruce |
{4} {}+{} |
4 | 4 | |||||||||||
| 3 | β3 011 |
Octaedro 3-orthoplex Tricruce |
{3,4} {30,1,1} {}+{}+{} |
6 | 12 | 8 | ||||||||||
| 4 | β4 111 |
Hexadecacoron 4-orthoplex Tetracruce |
{3,3,4} {31,1,1} 4{} |
8 | 24 | 32 | 16 | |||||||||
| 5 | β5 211 |
5-ortoplex Pentacruce |
{33,4} {32,1,1} 5{} |
10 | 40 | 80 | 80 | 32 | ||||||||
| 6 | β6 311 |
6-ortoplex Hexacruce |
{34,4} {33,1,1} 6{} |
12 | 60 | 160 | 240 | 192 | 64 | |||||||
| 7 | β7 411 |
7-ortoplex Heptacruce |
{35,4} {34,1,1} 7{} |
14 | 84 | 280 | 560 | 672 | 448 | 128 | ||||||
| 8 | β8 511 |
8-ortoplex Octacruce |
{36,4} {35,1,1} 8{} |
16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | |||||
| 9 | β9 611 |
9-ortoplex Eneacruce |
{37,4} {36,1,1} 9{} |
18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | ||||
| 10 | β10 711 |
10-ortoplex Decacruce |
{38,4} {37,1,1} 10{} |
20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | |||
| ... | ||||||||||||||||
| n | βn k11 |
n-ortoplex n-cruce |
{3n − 2,4} {3n − 3,1,1} n{} |
2n 0-caras, ... k-caras ..., 2n (n-1)-caras | ||||||||||||
Los vértices de un politopo de cruz alineado según los ejes están todos a igual distancia unos de otros en la Distancia Manhattan (L1 norm). La Conjetura de Kusner's afirma que afirma que este conjunto de puntos 2D es el mayor conjunto equidistante posible para esta distancia.[1]
Véase también
editar- Portal:Matemática. Contenido relacionado con Matemática.
- Portal:Geometría. Contenido relacionado con Geometría.
Referencias
editarBibliografía
editar- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed. edición). New York: Dover Publications. pp. 121–122. ISBN 0-486-61480-8. p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
Enlaces externos
editar- Wikimedia Commons alberga una categoría multimedia sobre Politopo de cruce.
- Weisstein, Eric W. «Cross polytope». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Polytope Viewer (Click <polytopes...> to select cross polytope.)