|
| 1 | +--- |
| 2 | +title: LFUCache |
| 3 | +type: docs |
| 4 | +--- |
| 5 | + |
| 6 | +# 最不经常最少使用 LFUCache |
| 7 | + |
| 8 | +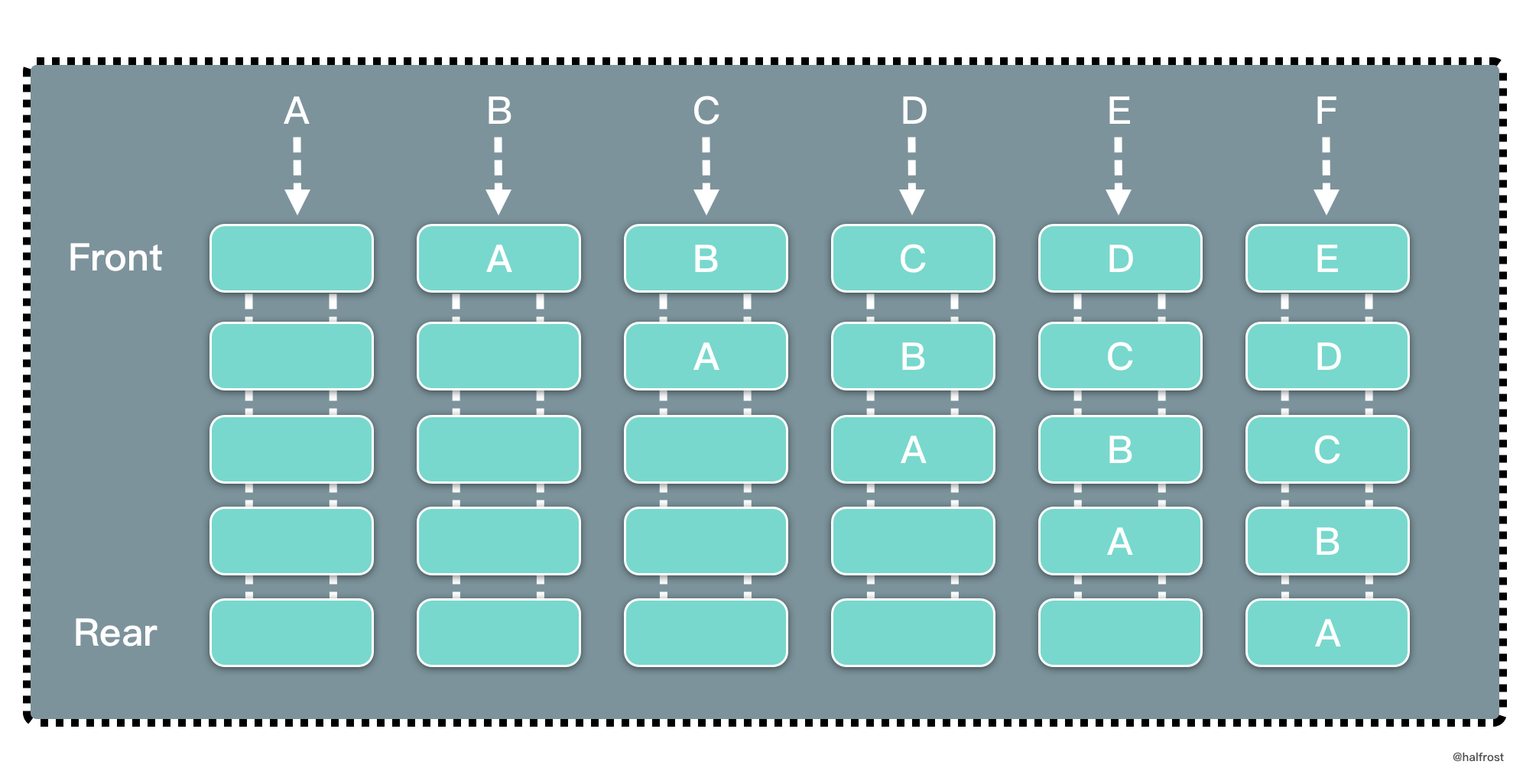 |
| 9 | + |
| 10 | +LFU 是 Least Frequently Used 的缩写,即最不经常最少使用,也是一种常用的页面置换算法,选择访问计数器最小的页面予以淘汰。如下图,缓存中每个页面带一个访问计数器。 |
| 11 | + |
| 12 | + |
| 13 | +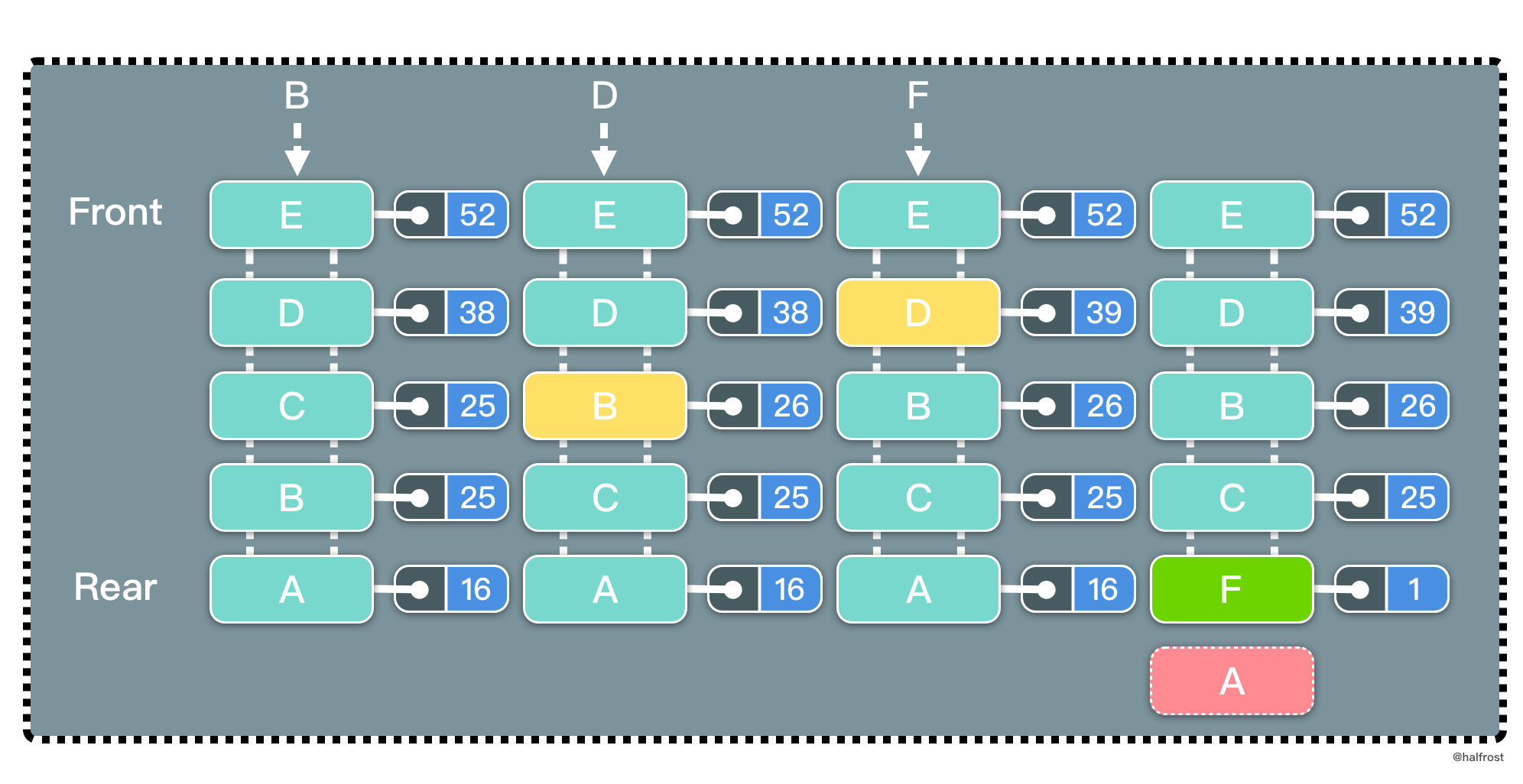 |
| 14 | + |
| 15 | +根据 LFU 的策略,每访问一次都要更新访问计数器。当插入 B 的时候,发现缓存中有 B,所以增加访问计数器的计数,并把 B 移动到访问计数器从大到小排序的地方。再插入 D,同理先更新计数器,再移动到它排序以后的位置。当插入 F 的时候,缓存中不存在 F,所以淘汰计数器最小的页面的页面,所以淘汰 A 页面。此时 F 排在最下面,计数为 1。 |
| 16 | + |
| 17 | +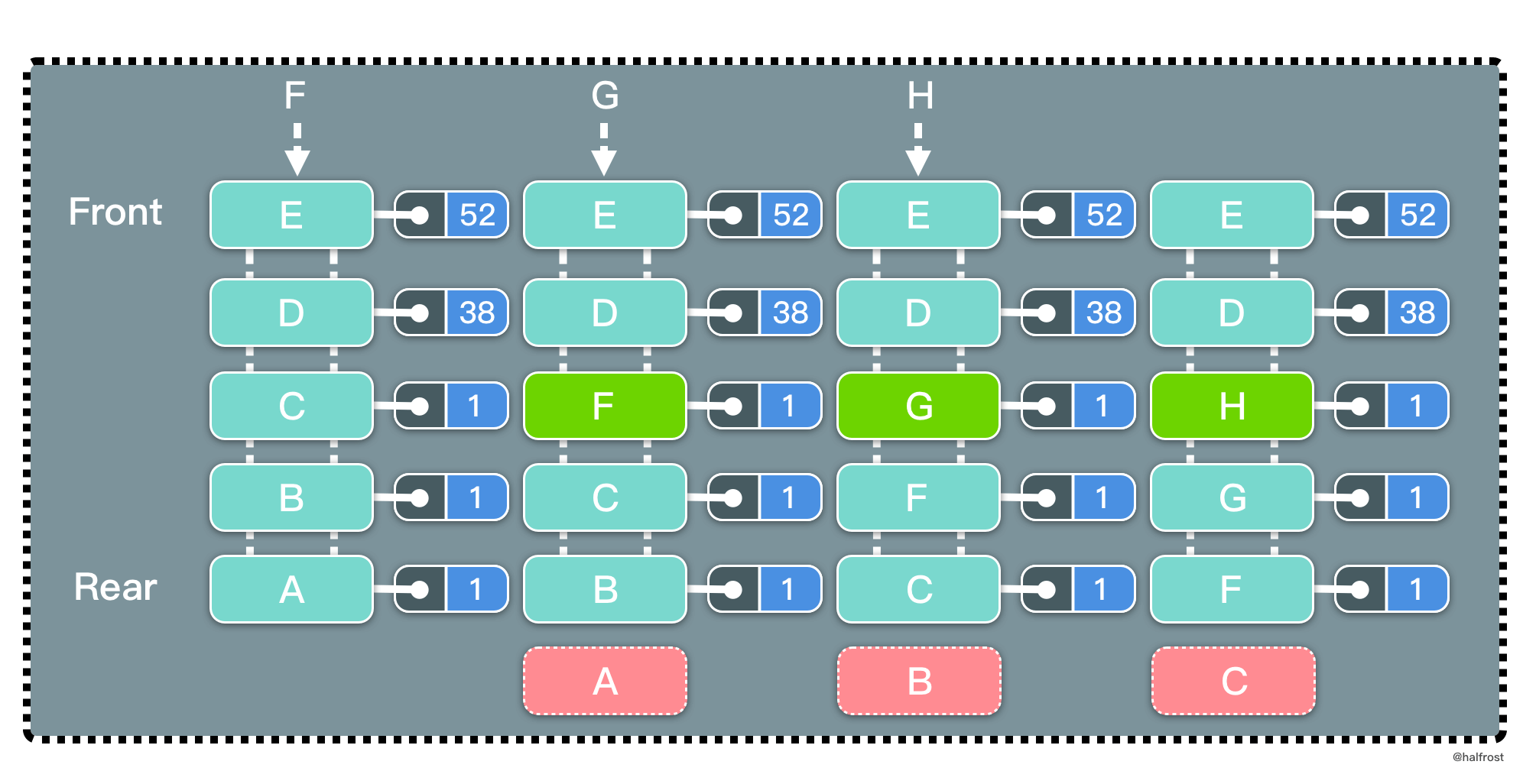 |
| 18 | + |
| 19 | +这里有一个比 LRU 特别的地方。如果淘汰的页面访问次数有多个相同的访问次数,选择最靠尾部的。如上图中,A、B、C 三者的访问次数相同,都是 1 次。要插入 F,F 不在缓存中,此时要淘汰 A 页面。F 是新插入的页面,访问次数为 1,排在 C 的前面。也就是说相同的访问次数,按照新旧顺序排列,淘汰掉最旧的页面。这一点是和 LRU 最大的不同的地方。 |
| 20 | + |
| 21 | +可以发现,**LFU 更新和插入新页面可以发生在链表中任意位置,删除页面都发生在表尾**。 |
| 22 | + |
| 23 | + |
| 24 | +## 解法一 Get O(1) / Put O(1) |
| 25 | + |
| 26 | +LFU 同样要求查询尽量高效,O(1) 内查询。依旧选用 map 查询。修改和删除也需要 O(1) 完成,依旧选用双向链表,继续复用 container 包中的 list 数据结构。LFU 需要记录访问次数,所以每个结点除了存储 key,value,需要再多存储 frequency 访问次数。 |
| 27 | + |
| 28 | +还有 1 个问题需要考虑,一个是如何按频次排序?相同频次,按照先后顺序排序。如果你开始考虑排序算法的话,思考方向就偏离最佳答案了。排序至少 O(nlogn)。重新回看 LFU 的工作原理,会发现它只关心最小频次。其他频次之间的顺序并不关心。所以不需要排序。用一个 min 变量保存最小频次,淘汰时读取这个最小值能找到要删除的结点。相同频次按照先后顺序排列,这个需求还是用双向链表实现,双向链表插入的顺序体现了结点的先后顺序。相同频次对应一个双向链表,可能有多个相同频次,所以可能有多个双向链表。用一个 map 维护访问频次和双向链表的对应关系。删除最小频次时,通过 min 找到最小频次,然后再这个 map 中找到这个频次对应的双向链表,在双向链表中找到最旧的那个结点删除。这就解决了 LFU 删除操作。 |
| 29 | + |
| 30 | +LFU 的更新操作和 LRU 类似,也需要用一个 map 保存 key 和双向链表结点的映射关系。这个双向链表结点中存储的是 key-value-frequency 三个元素的元组。这样通过结点中的 key 和 frequency 可以反过来删除 map 中的 key。 |
| 31 | + |
| 32 | +定义 LFUCache 的数据结构如下: |
| 33 | + |
| 34 | +```go |
| 35 | + |
| 36 | +import "container/list" |
| 37 | + |
| 38 | +type LFUCache struct { |
| 39 | + nodes map[int]*list.Element |
| 40 | + lists map[int]*list.List |
| 41 | + capacity int |
| 42 | + min int |
| 43 | +} |
| 44 | + |
| 45 | +type node struct { |
| 46 | + key int |
| 47 | + value int |
| 48 | + frequency int |
| 49 | +} |
| 50 | + |
| 51 | +func Constructor(capacity int) LFUCache { |
| 52 | + return LFUCache{nodes: make(map[int]*list.Element), |
| 53 | + lists: make(map[int]*list.List), |
| 54 | + capacity: capacity, |
| 55 | + min: 0, |
| 56 | + } |
| 57 | +} |
| 58 | + |
| 59 | +``` |
| 60 | + |
| 61 | +LFUCache 的 Get 操作涉及更新 frequency 值和 2 个 map。在 nodes map 中通过 key 获取到结点信息。在 lists 删除结点当前 frequency 结点。删完以后 frequency ++。新的 frequency 如果在 lists 中存在,添加到双向链表表首,如果不存在,需要新建一个双向链表并把当前结点加到表首。再更新双向链表结点作为 value 的 map。最后更新 min 值,判断老的 frequency 对应的双向链表中是否已经为空,如果空了,min++。 |
| 62 | + |
| 63 | +```go |
| 64 | +func (this *LFUCache) Get(key int) int { |
| 65 | + value, ok := this.nodes[key] |
| 66 | + if !ok { |
| 67 | + return -1 |
| 68 | + } |
| 69 | + currentNode := value.Value.(*node) |
| 70 | + this.lists[currentNode.frequency].Remove(value) |
| 71 | + currentNode.frequency++ |
| 72 | + if _, ok := this.lists[currentNode.frequency]; !ok { |
| 73 | + this.lists[currentNode.frequency] = list.New() |
| 74 | + } |
| 75 | + newList := this.lists[currentNode.frequency] |
| 76 | + newNode := newList.PushFront(currentNode) |
| 77 | + this.nodes[key] = newNode |
| 78 | + if currentNode.frequency-1 == this.min && this.lists[currentNode.frequency-1].Len() == 0 { |
| 79 | + this.min++ |
| 80 | + } |
| 81 | + return currentNode.value |
| 82 | +} |
| 83 | + |
| 84 | +``` |
| 85 | + |
| 86 | +LFU 的 Put 操作逻辑稍微多一点。先在 nodes map 中查询 key 是否存在,如果存在,获取这个结点,更新它的 value 值,然后手动调用一次 Get 操作,因为下面的更新逻辑和 Get 操作一致。如果 map 中不存在,接下来进行插入或者删除操作。判断 capacity 是否装满,如果装满,执行删除操作。在 min 对应的双向链表中删除表尾的结点,对应的也要删除 nodes map 中的键值。 |
| 87 | + |
| 88 | +由于新插入的页面访问次数一定为 1,所以 min 此时置为 1。新建结点,插入到 2 个 map 中。 |
| 89 | + |
| 90 | +```go |
| 91 | + |
| 92 | +func (this *LFUCache) Put(key int, value int) { |
| 93 | + if this.capacity == 0 { |
| 94 | + return |
| 95 | + } |
| 96 | + // 如果存在,更新访问次数 |
| 97 | + if currentValue, ok := this.nodes[key]; ok { |
| 98 | + currentNode := currentValue.Value.(*node) |
| 99 | + currentNode.value = value |
| 100 | + this.Get(key) |
| 101 | + return |
| 102 | + } |
| 103 | + // 如果不存在且缓存满了,需要删除 |
| 104 | + if this.capacity == len(this.nodes) { |
| 105 | + currentList := this.lists[this.min] |
| 106 | + backNode := currentList.Back() |
| 107 | + delete(this.nodes, backNode.Value.(*node).key) |
| 108 | + currentList.Remove(backNode) |
| 109 | + } |
| 110 | + // 新建结点,插入到 2 个 map 中 |
| 111 | + this.min = 1 |
| 112 | + currentNode := &node{ |
| 113 | + key: key, |
| 114 | + value: value, |
| 115 | + frequency: 1, |
| 116 | + } |
| 117 | + if _, ok := this.lists[1]; !ok { |
| 118 | + this.lists[1] = list.New() |
| 119 | + } |
| 120 | + newList := this.lists[1] |
| 121 | + newNode := newList.PushFront(currentNode) |
| 122 | + this.nodes[key] = newNode |
| 123 | +} |
| 124 | + |
| 125 | +``` |
| 126 | + |
| 127 | +总结,LFU 是由两个 map 和一个 min 指针组成的数据结构。一个 map 中 key 存的是访问次数,对应的 value 是一个个的双向链表,此处双向链表的作用是在相同频次的情况下,淘汰表尾最旧的那个页面。另一个 map 中 key 对应的 value 是双向链表的结点,结点中比 LRU 多存储了一个访问次数的值,即结点中存储 key-value-frequency 的元组。此处双向链表的作用和 LRU 是类似的,可以根据 map 中的 key 更新双向链表结点中的 value 和 frequency 的值,也可以根据双向链表结点中的 key 和 frequency 反向更新 map 中的对应关系。如下图: |
| 128 | + |
| 129 | + |
| 130 | + |
| 131 | +提交代码以后,成功通过所有测试用例。 |
| 132 | + |
| 133 | + |
| 134 | + |
| 135 | + |
| 136 | + |
| 137 | +## 解法二 Get O(capacity) / Put O(capacity) |
| 138 | + |
| 139 | +LFU 的另外一个思路是利用 [Index Priority Queue](https://algs4.cs.princeton.edu/24pq/) 这个数据结构。别被名字吓到,Index Priority Queue = map + Priority Queue,仅此而已。 |
| 140 | + |
| 141 | +利用 Priority Queue 维护一个最小堆,堆顶是访问次数最小的元素。map 中的 value 存储的是优先队列中结点。 |
| 142 | + |
| 143 | +```go |
| 144 | +import "container/heap" |
| 145 | + |
| 146 | +type LFUCache struct { |
| 147 | + capacity int |
| 148 | + pq PriorityQueue |
| 149 | + hash map[int]*Item |
| 150 | + counter int |
| 151 | +} |
| 152 | + |
| 153 | +func Constructor(capacity int) LFUCache { |
| 154 | + lfu := LFUCache{ |
| 155 | + pq: PriorityQueue{}, |
| 156 | + hash: make(map[int]*Item, capacity), |
| 157 | + capacity: capacity, |
| 158 | + } |
| 159 | + return lfu |
| 160 | +} |
| 161 | + |
| 162 | +``` |
| 163 | + |
| 164 | +Get 和 Put 操作要尽量的快,有 2 个问题需要解决。当访问次数相同时,如何删除掉最久的元素?当元素的访问次数发生变化时,如何快速调整堆?为了解决这 2 个问题,定义如下的数据结构: |
| 165 | + |
| 166 | +```go |
| 167 | +// An Item is something we manage in a priority queue. |
| 168 | +type Item struct { |
| 169 | + value int // The value of the item; arbitrary. |
| 170 | + key int |
| 171 | + frequency int // The priority of the item in the queue. |
| 172 | + count int // use for evicting the oldest element |
| 173 | + // The index is needed by update and is maintained by the heap.Interface methods. |
| 174 | + index int // The index of the item in the heap. |
| 175 | +} |
| 176 | + |
| 177 | +``` |
| 178 | + |
| 179 | +堆中的结点存储这 5 个值。count 值用来决定哪个是最老的元素,类似一个操作时间戳。index 值用来 re-heapify 调整堆的。接下来实现 PriorityQueue 的方法。 |
| 180 | + |
| 181 | +```go |
| 182 | +// A PriorityQueue implements heap.Interface and holds Items. |
| 183 | +type PriorityQueue []*Item |
| 184 | + |
| 185 | +func (pq PriorityQueue) Len() int { return len(pq) } |
| 186 | + |
| 187 | +func (pq PriorityQueue) Less(i, j int) bool { |
| 188 | + // We want Pop to give us the highest, not lowest, priority so we use greater than here. |
| 189 | + if pq[i].frequency == pq[j].frequency { |
| 190 | + return pq[i].count < pq[j].count |
| 191 | + } |
| 192 | + return pq[i].frequency < pq[j].frequency |
| 193 | +} |
| 194 | + |
| 195 | +func (pq PriorityQueue) Swap(i, j int) { |
| 196 | + pq[i], pq[j] = pq[j], pq[i] |
| 197 | + pq[i].index = i |
| 198 | + pq[j].index = j |
| 199 | +} |
| 200 | + |
| 201 | +func (pq *PriorityQueue) Push(x interface{}) { |
| 202 | + n := len(*pq) |
| 203 | + item := x.(*Item) |
| 204 | + item.index = n |
| 205 | + *pq = append(*pq, item) |
| 206 | +} |
| 207 | + |
| 208 | +func (pq *PriorityQueue) Pop() interface{} { |
| 209 | + old := *pq |
| 210 | + n := len(old) |
| 211 | + item := old[n-1] |
| 212 | + old[n-1] = nil // avoid memory leak |
| 213 | + item.index = -1 // for safety |
| 214 | + *pq = old[0 : n-1] |
| 215 | + return item |
| 216 | +} |
| 217 | + |
| 218 | +// update modifies the priority and value of an Item in the queue. |
| 219 | +func (pq *PriorityQueue) update(item *Item, value int, frequency int, count int) { |
| 220 | + item.value = value |
| 221 | + item.count = count |
| 222 | + item.frequency = frequency |
| 223 | + heap.Fix(pq, item.index) |
| 224 | +} |
| 225 | +``` |
| 226 | + |
| 227 | +在 Less() 方法中,frequency 从小到大排序,frequency 相同的,按 count 从小到大排序。按照优先队列建堆规则,可以得到,frequency 最小的在堆顶,相同的 frequency,count 最小的越靠近堆顶。 |
| 228 | + |
| 229 | +在 Swap() 方法中,记得要更新 index 值。在 Push() 方法中,插入时队列的长度即是该元素的 index 值,此处也要记得更新 index 值。update() 方法调用 Fix() 函数。Fix() 函数比先 Remove() 再 Push() 一个新的值,花销要小。所以此处调用 Fix() 函数,这个操作的时间复杂度是 O(log n)。 |
| 230 | + |
| 231 | +这样就维护了最小 Index Priority Queue。Get 操作非常简单: |
| 232 | + |
| 233 | +```go |
| 234 | +func (this *LFUCache) Get(key int) int { |
| 235 | + if this.capacity == 0 { |
| 236 | + return -1 |
| 237 | + } |
| 238 | + if item, ok := this.hash[key]; ok { |
| 239 | + this.counter++ |
| 240 | + this.pq.update(item, item.value, item.frequency+1, this.counter) |
| 241 | + return item.value |
| 242 | + } |
| 243 | + return -1 |
| 244 | +} |
| 245 | + |
| 246 | +``` |
| 247 | + |
| 248 | +在 hashmap 中查询 key,如果存在,counter 时间戳累加,调用 Priority Queue 的 update 方法,调整堆。 |
| 249 | + |
| 250 | +```go |
| 251 | +func (this *LFUCache) Put(key int, value int) { |
| 252 | + if this.capacity == 0 { |
| 253 | + return |
| 254 | + } |
| 255 | + this.counter++ |
| 256 | + // 如果存在,增加 frequency,再调整堆 |
| 257 | + if item, ok := this.hash[key]; ok { |
| 258 | + this.pq.update(item, value, item.frequency+1, this.counter) |
| 259 | + return |
| 260 | + } |
| 261 | + // 如果不存在且缓存满了,需要删除。在 hashmap 和 pq 中删除。 |
| 262 | + if len(this.pq) == this.capacity { |
| 263 | + item := heap.Pop(&this.pq).(*Item) |
| 264 | + delete(this.hash, item.key) |
| 265 | + } |
| 266 | + // 新建结点,在 hashmap 和 pq 中添加。 |
| 267 | + item := &Item{ |
| 268 | + value: value, |
| 269 | + key: key, |
| 270 | + count: this.counter, |
| 271 | + } |
| 272 | + heap.Push(&this.pq, item) |
| 273 | + this.hash[key] = item |
| 274 | +} |
| 275 | +``` |
| 276 | + |
| 277 | + |
| 278 | +用最小堆实现的 LFU,Put 时间复杂度是 O(capacity),Get 时间复杂度是 O(capacity),不及 2 个 map 实现的版本。巧的是最小堆的版本居然打败了 100%。 |
| 279 | + |
| 280 | +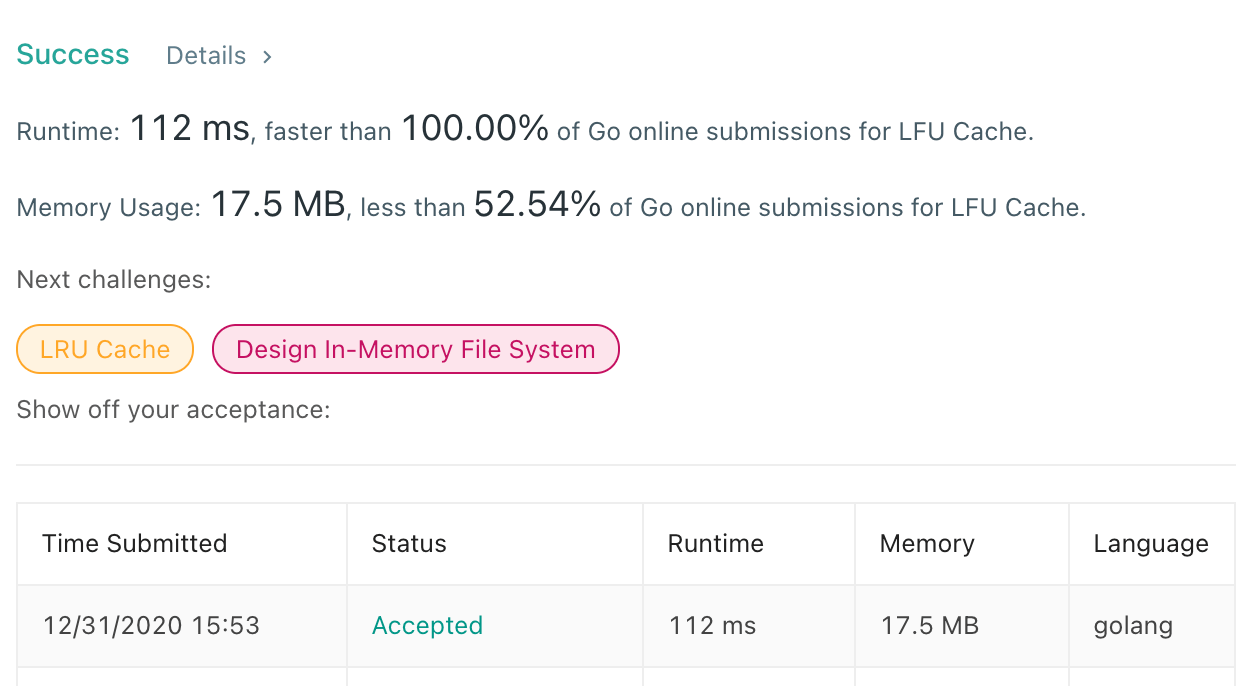 |
| 281 | + |
| 282 | + |
| 283 | +## 模板 |
| 284 | + |
| 285 | + |
| 286 | +```go |
| 287 | +import "container/list" |
| 288 | + |
| 289 | +type LFUCache struct { |
| 290 | + nodes map[int]*list.Element |
| 291 | + lists map[int]*list.List |
| 292 | + capacity int |
| 293 | + min int |
| 294 | +} |
| 295 | + |
| 296 | +type node struct { |
| 297 | + key int |
| 298 | + value int |
| 299 | + frequency int |
| 300 | +} |
| 301 | + |
| 302 | +func Constructor(capacity int) LFUCache { |
| 303 | + return LFUCache{nodes: make(map[int]*list.Element), |
| 304 | + lists: make(map[int]*list.List), |
| 305 | + capacity: capacity, |
| 306 | + min: 0, |
| 307 | + } |
| 308 | +} |
| 309 | + |
| 310 | +func (this *LFUCache) Get(key int) int { |
| 311 | + value, ok := this.nodes[key] |
| 312 | + if !ok { |
| 313 | + return -1 |
| 314 | + } |
| 315 | + currentNode := value.Value.(*node) |
| 316 | + this.lists[currentNode.frequency].Remove(value) |
| 317 | + currentNode.frequency++ |
| 318 | + if _, ok := this.lists[currentNode.frequency]; !ok { |
| 319 | + this.lists[currentNode.frequency] = list.New() |
| 320 | + } |
| 321 | + newList := this.lists[currentNode.frequency] |
| 322 | + newNode := newList.PushBack(currentNode) |
| 323 | + this.nodes[key] = newNode |
| 324 | + if currentNode.frequency-1 == this.min && this.lists[currentNode.frequency-1].Len() == 0 { |
| 325 | + this.min++ |
| 326 | + } |
| 327 | + return currentNode.value |
| 328 | +} |
| 329 | + |
| 330 | +func (this *LFUCache) Put(key int, value int) { |
| 331 | + if this.capacity == 0 { |
| 332 | + return |
| 333 | + } |
| 334 | + if currentValue, ok := this.nodes[key]; ok { |
| 335 | + currentNode := currentValue.Value.(*node) |
| 336 | + currentNode.value = value |
| 337 | + this.Get(key) |
| 338 | + return |
| 339 | + } |
| 340 | + if this.capacity == len(this.nodes) { |
| 341 | + currentList := this.lists[this.min] |
| 342 | + frontNode := currentList.Front() |
| 343 | + delete(this.nodes, frontNode.Value.(*node).key) |
| 344 | + currentList.Remove(frontNode) |
| 345 | + } |
| 346 | + this.min = 1 |
| 347 | + currentNode := &node{ |
| 348 | + key: key, |
| 349 | + value: value, |
| 350 | + frequency: 1, |
| 351 | + } |
| 352 | + if _, ok := this.lists[1]; !ok { |
| 353 | + this.lists[1] = list.New() |
| 354 | + } |
| 355 | + newList := this.lists[1] |
| 356 | + newNode := newList.PushBack(currentNode) |
| 357 | + this.nodes[key] = newNode |
| 358 | +} |
| 359 | + |
| 360 | +``` |
0 commit comments