|
| 1 | +# [1203. Sort Items by Groups Respecting Dependencies](https://leetcode.com/problems/sort-items-by-groups-respecting-dependencies/) |
| 2 | + |
| 3 | + |
| 4 | +## 题目 |
| 5 | + |
| 6 | +There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`-th item belongs to and it's equal to `-1` if the `i`-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it. |
| 7 | + |
| 8 | +Return a sorted list of the items such that: |
| 9 | + |
| 10 | +- The items that belong to the same group are next to each other in the sorted list. |
| 11 | +- There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`th item in the sorted array (to the left of the `i`th item). |
| 12 | + |
| 13 | +Return any solution if there is more than one solution and return an **empty list** if there is no solution. |
| 14 | + |
| 15 | +**Example 1:** |
| 16 | + |
| 17 | + |
| 18 | + |
| 19 | +``` |
| 20 | +Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]] |
| 21 | +Output: [6,3,4,1,5,2,0,7] |
| 22 | +
|
| 23 | +``` |
| 24 | + |
| 25 | +**Example 2:** |
| 26 | + |
| 27 | +``` |
| 28 | +Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]] |
| 29 | +Output: [] |
| 30 | +Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list. |
| 31 | +
|
| 32 | +``` |
| 33 | + |
| 34 | +**Constraints:** |
| 35 | + |
| 36 | +- `1 <= m <= n <= 3 * 104` |
| 37 | +- `group.length == beforeItems.length == n` |
| 38 | +- `1 <= group[i] <= m - 1` |
| 39 | +- `0 <= beforeItems[i].length <= n - 1` |
| 40 | +- `0 <= beforeItems[i][j] <= n - 1` |
| 41 | +- `i != beforeItems[i][j]` |
| 42 | +- `beforeItems[i]` does not contain duplicates elements. |
| 43 | + |
| 44 | +## 题目大意 |
| 45 | + |
| 46 | +有 n 个项目,每个项目或者不属于任何小组,或者属于 m 个小组之一。group[i] 表示第 i 个小组所属的小组,如果第 i 个项目不属于任何小组,则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目,即没有任何项目属于这个小组。 |
| 47 | + |
| 48 | +请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表: |
| 49 | + |
| 50 | +- 同一小组的项目,排序后在列表中彼此相邻。 |
| 51 | +- 项目之间存在一定的依赖关系,我们用一个列表 beforeItems 来表示,其中 beforeItems[i] 表示在进行第 i 个项目前(位于第 i 个项目左侧)应该完成的所有项目。 |
| 52 | + |
| 53 | +如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。 |
| 54 | + |
| 55 | +## 解题思路 |
| 56 | + |
| 57 | +- 读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是,同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序,第二次拓扑排序排出组内的顺序。为了实现方便,用 map 给虚拟分组标记编号。如下图,将 3,4,6 三个任务打包到 0 号分组里面,将 2,5 两个任务打包到 1 号分组里面,其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里,所以 3 号分组依赖 0 号分组。先组间排序,确定分组顺序,再组内拓扑排序,排出最终顺序。 |
| 58 | + |
| 59 | + 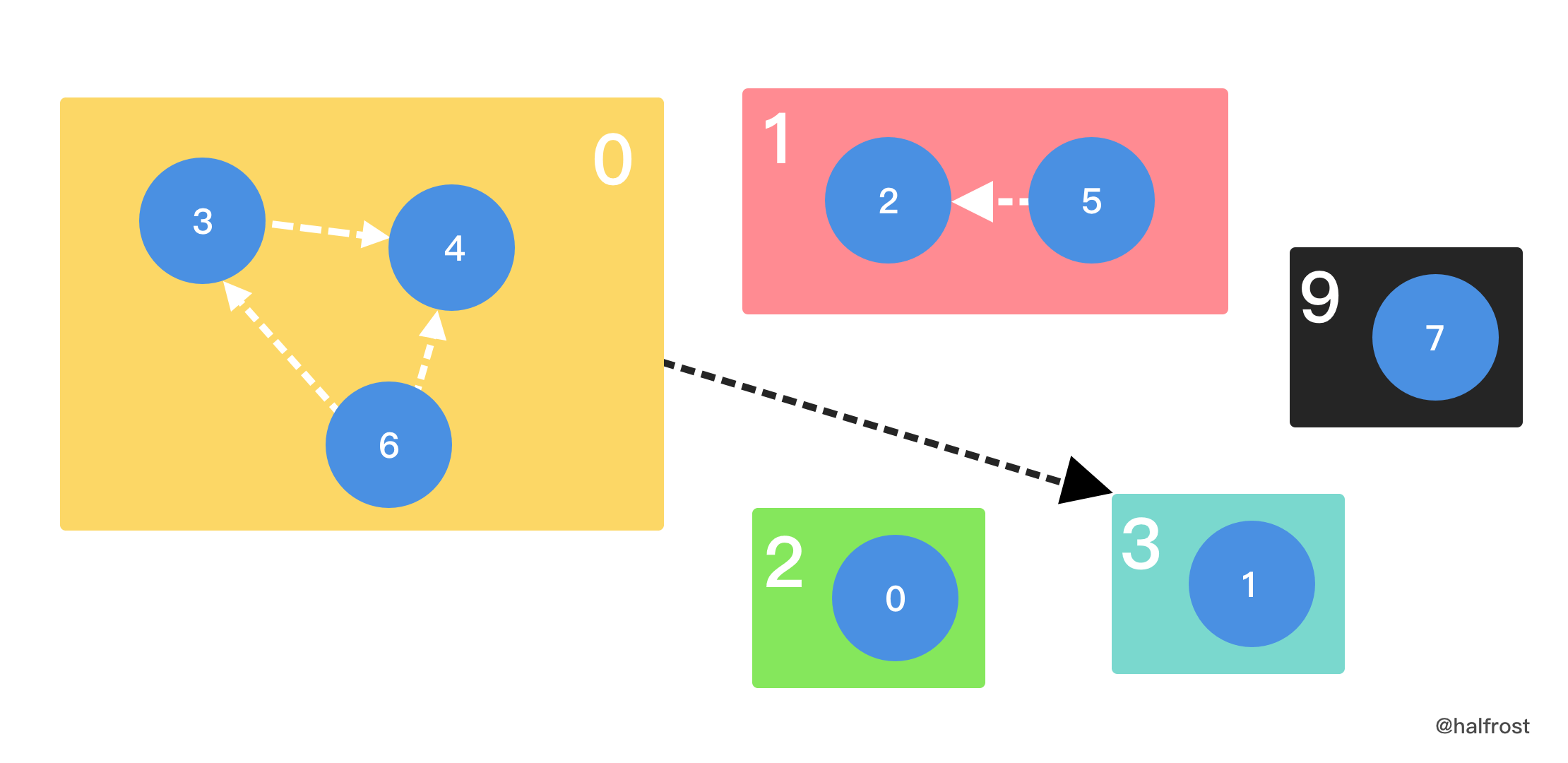 |
| 60 | + |
| 61 | +- 上面的解法可以 AC,但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢?将必须要在一起的结点统一依赖一个虚拟结点,例如下图中的虚拟结点 8 和 9 。3,4,6 都依赖 8 号任务,2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务,由于 6 由依赖 8 ,所以添加 1 依赖 8 的边。通过增加虚拟结点,增加了需要打包在一起结点的入度。构建出以上关系以后,按照入度为 0 的原则,依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ,对它们进行 DFS,必定会使得与它关联的节点都被安排在一起,这样就满足了题意:同一小组的项目,排序后在列表中彼此相邻。一遍扫完,满足题意的顺序就排出来了。这个解法 beat 100%! |
| 62 | + |
| 63 | + 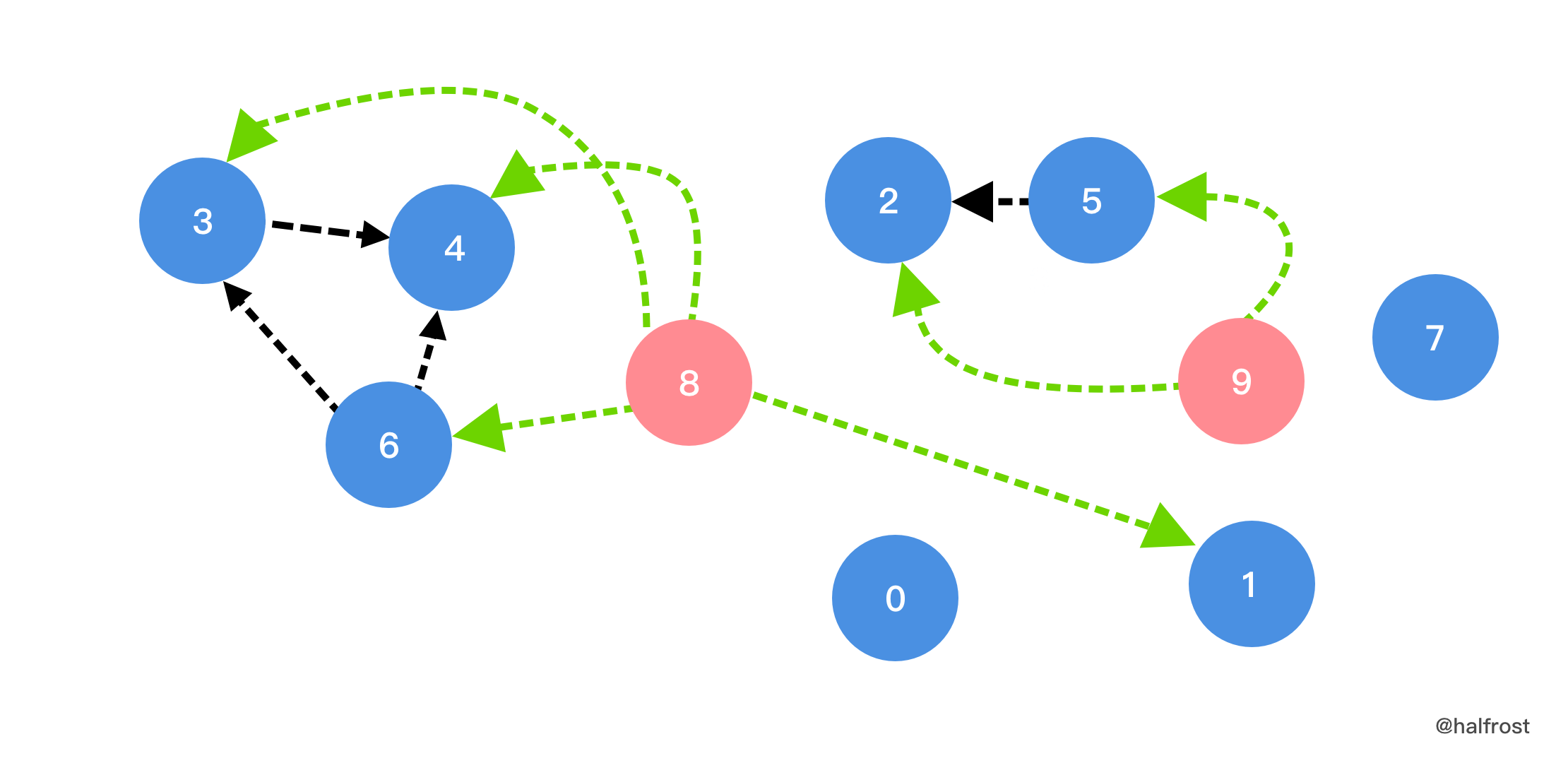 |
| 64 | + |
| 65 | +## 代码 |
| 66 | + |
| 67 | +```go |
| 68 | +package leetcode |
| 69 | + |
| 70 | +// 解法一 拓扑排序版的 DFS |
| 71 | +func sortItems(n int, m int, group []int, beforeItems [][]int) []int { |
| 72 | + groups, inDegrees := make([][]int, n+m), make([]int, n+m) |
| 73 | + for i, g := range group { |
| 74 | + if g > -1 { |
| 75 | + g += n |
| 76 | + groups[g] = append(groups[g], i) |
| 77 | + inDegrees[i]++ |
| 78 | + } |
| 79 | + } |
| 80 | + for i, ancestors := range beforeItems { |
| 81 | + gi := group[i] |
| 82 | + if gi == -1 { |
| 83 | + gi = i |
| 84 | + } else { |
| 85 | + gi += n |
| 86 | + } |
| 87 | + for _, ancestor := range ancestors { |
| 88 | + ga := group[ancestor] |
| 89 | + if ga == -1 { |
| 90 | + ga = ancestor |
| 91 | + } else { |
| 92 | + ga += n |
| 93 | + } |
| 94 | + if gi == ga { |
| 95 | + groups[ancestor] = append(groups[ancestor], i) |
| 96 | + inDegrees[i]++ |
| 97 | + } else { |
| 98 | + groups[ga] = append(groups[ga], gi) |
| 99 | + inDegrees[gi]++ |
| 100 | + } |
| 101 | + } |
| 102 | + } |
| 103 | + res := []int{} |
| 104 | + for i, d := range inDegrees { |
| 105 | + if d == 0 { |
| 106 | + sortItemsDFS(i, n, &res, &inDegrees, &groups) |
| 107 | + } |
| 108 | + } |
| 109 | + if len(res) != n { |
| 110 | + return nil |
| 111 | + } |
| 112 | + return res |
| 113 | +} |
| 114 | + |
| 115 | +func sortItemsDFS(i, n int, res, inDegrees *[]int, groups *[][]int) { |
| 116 | + if i < n { |
| 117 | + *res = append(*res, i) |
| 118 | + } |
| 119 | + (*inDegrees)[i] = -1 |
| 120 | + for _, ch := range (*groups)[i] { |
| 121 | + if (*inDegrees)[ch]--; (*inDegrees)[ch] == 0 { |
| 122 | + sortItemsDFS(ch, n, res, inDegrees, groups) |
| 123 | + } |
| 124 | + } |
| 125 | +} |
| 126 | + |
| 127 | +// 解法二 二维拓扑排序 时间复杂度 O(m+n),空间复杂度 O(m+n) |
| 128 | +func sortItems1(n int, m int, group []int, beforeItems [][]int) []int { |
| 129 | + groupItems, res := map[int][]int{}, []int{} |
| 130 | + for i := 0; i < len(group); i++ { |
| 131 | + if group[i] == -1 { |
| 132 | + group[i] = m + i |
| 133 | + } |
| 134 | + groupItems[group[i]] = append(groupItems[group[i]], i) |
| 135 | + } |
| 136 | + groupGraph, groupDegree, itemGraph, itemDegree := make([][]int, m+n), make([]int, m+n), make([][]int, n), make([]int, n) |
| 137 | + for i := 0; i < len(beforeItems); i++ { |
| 138 | + for j := 0; j < len(beforeItems[i]); j++ { |
| 139 | + if group[beforeItems[i][j]] != group[i] { |
| 140 | + // 不同组项目,确定组间依赖关系 |
| 141 | + groupGraph[group[beforeItems[i][j]]] = append(groupGraph[group[beforeItems[i][j]]], group[i]) |
| 142 | + groupDegree[group[i]]++ |
| 143 | + } else { |
| 144 | + // 同组项目,确定组内依赖关系 |
| 145 | + itemGraph[beforeItems[i][j]] = append(itemGraph[beforeItems[i][j]], i) |
| 146 | + itemDegree[i]++ |
| 147 | + } |
| 148 | + } |
| 149 | + } |
| 150 | + items := []int{} |
| 151 | + for i := 0; i < m+n; i++ { |
| 152 | + items = append(items, i) |
| 153 | + } |
| 154 | + // 组间拓扑 |
| 155 | + groupOrders := topSort(groupGraph, groupDegree, items) |
| 156 | + if len(groupOrders) < len(items) { |
| 157 | + return nil |
| 158 | + } |
| 159 | + for i := 0; i < len(groupOrders); i++ { |
| 160 | + items := groupItems[groupOrders[i]] |
| 161 | + // 组内拓扑 |
| 162 | + orders := topSort(itemGraph, itemDegree, items) |
| 163 | + if len(orders) < len(items) { |
| 164 | + return nil |
| 165 | + } |
| 166 | + res = append(res, orders...) |
| 167 | + } |
| 168 | + return res |
| 169 | +} |
| 170 | + |
| 171 | +func topSort(graph [][]int, deg, items []int) (orders []int) { |
| 172 | + q := []int{} |
| 173 | + for _, i := range items { |
| 174 | + if deg[i] == 0 { |
| 175 | + q = append(q, i) |
| 176 | + } |
| 177 | + } |
| 178 | + for len(q) > 0 { |
| 179 | + from := q[0] |
| 180 | + q = q[1:] |
| 181 | + orders = append(orders, from) |
| 182 | + for _, to := range graph[from] { |
| 183 | + deg[to]-- |
| 184 | + if deg[to] == 0 { |
| 185 | + q = append(q, to) |
| 186 | + } |
| 187 | + } |
| 188 | + } |
| 189 | + return |
| 190 | +} |
| 191 | +``` |
0 commit comments