|
| 1 | +## 1. 位运算简介 |
| 2 | + |
| 3 | +> **位运算(Bit Operation)**:在计算机内部,数是以「二进制(Binary)」的形式表示的。位运算就是直接对数的二进制进行计算操作,在程序中使用位运算进行操作,会大大提高程序的性能。 |
| 4 | +
|
| 5 | +- **二进制数(Binary)**:用 `0` 和 `1` 两个数码来表示的数,它的基数是 `2`,进位规则是「逢二进一」,借位规则是「借一当二」。例如,十进制中的 `1`、`2`、`3`、`4` 对应的二进制数分别为 `001`、`010`、`011`、`100`。 |
| 6 | + |
| 7 | +二进制数中的每一位数字称为「位(Bit)」, `3` 位所能表示的最大二进制数是 `111`,也就是十进制中的 `7`,即 $1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 7$。 |
| 8 | + |
| 9 | +在二进制的基础上,我们可以对二进制数进行相应的位运算。基本的位运算共 `6` 种,分别是:「按位与」、「按位或」、「按位异或」、「按位取反」、「左移」和「右移」。 |
| 10 | + |
| 11 | +## 2. 位运算基础操作 |
| 12 | + |
| 13 | +### 2.1 按位与运算 |
| 14 | + |
| 15 | +> **按位与运算(AND)**:按位与运算符 `&` 是双目运算符。其功能是对两个二进制数的每一个二进制位相与。只有对应的两个二进值位都为 `1` 时,结果位才为 `1`。当参与运算的是负数时,参与两个数均以补码出现。 |
| 16 | +
|
| 17 | +- 按位与运算规则: |
| 18 | + - `1 & 1 = 1` |
| 19 | + - `1 & 0 = 0` |
| 20 | + - `0 & 1 = 0` |
| 21 | + - `0 & 0 = 0` |
| 22 | + |
| 23 | +例如,十进制中的 `3` 和 `5` 进行按位与运算,则结果如图所示: |
| 24 | + |
| 25 | + |
| 26 | + |
| 27 | +按位与运算的通常用法: |
| 28 | + |
| 29 | +1. **清零**:任何数与 `0` 做按位与运算结果都为 `0`。 |
| 30 | + - `(x & 0) == 0`。 |
| 31 | +2. **取指定位**:比如要取一个数的低 `4` 位,则只需使用该数与二进制数 `00001111 (后 4 位为 1)`做按位与运算,结果就是这个数的低 `4` 位的值。 |
| 32 | +3. **奇偶判断**:通过与 `1` 进行按位与运算,即可判断某个数是奇数还是偶数。 |
| 33 | + - `(x & 1) == 0` 为偶数,`(x & 1) == 1` 为奇数。 |
| 34 | + |
| 35 | +### 2.2 按位或运算 |
| 36 | + |
| 37 | +> **按位或运算(OR)**:按位或运算符 `|` 是双目运算符。其功能对两个二进制数的每一个二进制位相或。只要对应的 `2` 个二进位有一个为 `1` 时,结果位就为 `1`。当参与运算的是负数时,参与两个数均以补码出现。 |
| 38 | +
|
| 39 | +- 按位或运算规则: |
| 40 | + - `1 | 1 = 1` |
| 41 | + - `1 | 0 = 1` |
| 42 | + - `0 | 1 = 1` |
| 43 | + - `0 | 0 = 0` |
| 44 | + |
| 45 | +例如,十进制中的 `3` 和 `5` 进行按位或运算,则结果如图所示: |
| 46 | + |
| 47 | + |
| 48 | + |
| 49 | +按位或运算的通常用法: |
| 50 | + |
| 51 | +1. **将某位设置为 `1`**:比如需要将一个数的低 `4` 位设置为 `1`,则只需使用该数与二进制数 `00001111 (后 4 位为 1)` 做按位或运算即可得到。 |
| 52 | + |
| 53 | +### 2.3 按位异或运算 |
| 54 | + |
| 55 | +> **按位异或运算(XOR)**:按位异或运算符 `^` 是双目运算符。其功能是对两个二进制数的每一个二进制位相异或。如果某位不相同则该位为 `1`,如果某位相同则该位为 `0`。当参与运算的是负数时,参与两个数均以补码出现。 |
| 56 | +
|
| 57 | +- 按位异或运算规则: |
| 58 | + - `0 ^ 0 = 0` |
| 59 | + - `1 ^ 0 = 1` |
| 60 | + - `0 ^ 1 = 1` |
| 61 | + - `1 ^ 1 = 0` |
| 62 | + |
| 63 | +例如,十进制中的 `3` 和 `5` 进行按位异或运算,则结果如图所示: |
| 64 | + |
| 65 | + |
| 66 | + |
| 67 | +按位异或运算的通常用法: |
| 68 | + |
| 69 | +1. **翻转指定位**:比如需要将一个数的低 `4` 位进行反转,则只需使用该数与二进制数 `00001111 (后 4 位为 1)` 做按位异或运算即可得到。 |
| 70 | +2. **与 `0` 相异或值不变**:一个数与 `0` 做按位异或运算的结果不变。例如,`10101100 ^ 00000000 = 10101100`。 |
| 71 | +3. **交换两个数**:通过按位异或运算可以实现交换两个数的目的。 |
| 72 | + |
| 73 | +```Python |
| 74 | +a, b = 10, 20 |
| 75 | +a ^= b |
| 76 | +b ^= a |
| 77 | +a ^= b |
| 78 | +print(a, b) |
| 79 | +``` |
| 80 | + |
| 81 | +### 2.4 按位取反运算 |
| 82 | + |
| 83 | +>**按位取反运算(NOT)**:按位取反运算符 `~` 是单目运算符。其功能是对一个二进制数的每一个二进制位取反。使数字 `1` 变为 `0`,`0` 变为 `1`。当参与运算的是负数时,参与的该数以补码出现。 |
| 84 | +
|
| 85 | +- 按位取反运算规则: |
| 86 | + - `~0 = 1` |
| 87 | + - `~1 = 0` |
| 88 | + |
| 89 | +例如,十进制中的 `3` 进行按位取反运算,则结果如图所示: |
| 90 | + |
| 91 | + |
| 92 | + |
| 93 | +### 2.5 按位左移运算 |
| 94 | + |
| 95 | +> **按位左移运算(SHL)**: 按位左移运算符 `<<` 是双目运算符。其功能是对一个二进制数的各个二进制位全部左移若干位(左边的二进制位丢弃,右边末尾补 `0`)。 |
| 96 | +
|
| 97 | +例如,十进制中的 `3` 进行左移 `1` 位运算,则结果如图所示: |
| 98 | + |
| 99 | +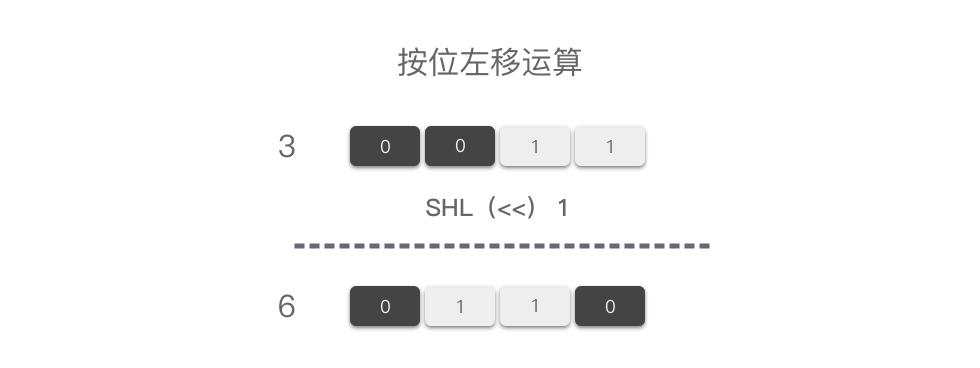 |
| 100 | + |
| 101 | +### 2.6 按位右移运算 |
| 102 | + |
| 103 | +> **按位右移运算(SHR)**: 按位右移运算符 `>>` 是双目运算符。其功能是对一个二进制数的各个二进制位全部右移若干位(右边的二进制位丢弃,正数左边开补 `0`,负数左边补 `1`)。 |
| 104 | +
|
| 105 | +例如,十进制中的 `3` 进行右移 `1` 位运算,则结果如图所示: |
| 106 | + |
| 107 | + |
| 108 | + |
| 109 | +## 2. 位运算的应用 |
| 110 | + |
| 111 | +### 2.1 位运算的常用应用 |
| 112 | + |
| 113 | +| 功 能 | 位运算 | 示例 | |
| 114 | +| ----------------------------------------- | -------------------------------- | ---------------------- | |
| 115 | +| **去掉最后一位** | <code>x >> 1</code> | `101101 -> 10110` | |
| 116 | +| **在最后加一个 `0`** | <code>x << 1</code> | `101101 -> 1011010` | |
| 117 | +| **在最后加一个 `1`** | <code>(x << 1) + 1</code> | `101101 -> 1011011` | |
| 118 | +| **把最后一位变成 `1`** | <code>x | 1</code> | `101100 -> 101101` | |
| 119 | +| **把最后一位变成 `0`** | <code>x | 1 - 1</code> | `101101 -> 101100` | |
| 120 | +| **最后一位取反** | <code>x ^ 1</code> | `101101 -> 101100` | |
| 121 | +| **把右数第 `k` 位变成 `1`** | <code>x | (1 << (k - 1))</code> | `101001 -> 101101, k = 3` | |
| 122 | +| **把右数第 `k` 位变成 `0`** | <code>x & ~(1 << (k - 1))</code> | `101101 -> 101001, k = 3` | |
| 123 | +| **右数第 `k` 位取反** | <code>x ^ (1 << (k - 1))</code> | `101001 -> 101101, k = 3` | |
| 124 | +| **取末尾 `3` 位** | <code>x & 7</code> | `1101101 -> 101` | |
| 125 | +| **取末尾 `k` 位** | <code>x & 15</code> | `1101101 -> 1101, k = 4` | |
| 126 | +| **取右数第 `k` 位** | <code>x >> (k - 1) & 1</code> | `1101101 -> 1, k = 4` | |
| 127 | +| **把末尾 `k` 位变成 `1`** | <code>x | (1 << k - 1)</code> | `101001 -> 101111, k = 4` | |
| 128 | +| **末尾 `k` 位取反** | <code>x ^ (1 << k - 1)</code> | `101001 -> 100110, k = 4` | |
| 129 | +| **把右边连续的 `1` 变成 `0`** | <code>x & (x + 1)</code> | `100101111 -> 100100000` | |
| 130 | +| **把右边起第一个 `0` 变成 `1`** | <code>x | (x + 1)</code> | `100101111 -> 100111111` | |
| 131 | +| **把右边连续的 `0` 变成 `1`** | <code>x | (x - 1)</code> | `11011000 -> 11011111` | |
| 132 | +| **只保留右边连续的 `1`** | <code>(x ^ (x + 1)) >> 1</code> | `100101111 -> 1111` | |
| 133 | +| **去掉右边起第一个 `1` 的左边** | <code>x & (x ^ (x - 1))</code> 或 <code>x & (-x)</code> | `100101000 -> 1000` | |
| 134 | +| **从右边开始,把最后一个 `1` 改写成 `0`** | <code>x & (x - 1)</code> | `100101000 -> 100100000` | |
| 135 | + |
| 136 | +### 2.1 Brian Kernighan 算法 |
| 137 | + |
| 138 | + |
| 139 | + |
| 140 | +## 参考资料 |
| 141 | + |
| 142 | +- 【博文】[Python 中的按位运算符 |【生长吧!Python!】- 云社区 - 华为云](https://bbs.huaweicloud.com/blogs/280901) |
| 143 | +- 【博文】[一文读懂位运算的使用 - 小黑说 Java - 掘金](https://juejin.cn/post/7011407264581943326) |
0 commit comments