|
1 | | -# 方法一:辅助矩阵 |
| 1 | +## 解题思路: |
2 | 2 |
|
3 | | -如下图所示,矩阵顺时针旋转 90º 后,可找到以下规律: |
| 3 | +设窗口区间为 $[i, j]$ ,最大值为 $x_j$ 。当窗口向前移动一格,则区间变为 $[i+1,j+1]$ ,即添加了 $nums[j + 1]$ ,删除了 $nums[i]$ 。 |
4 | 4 |
|
5 | | -- 「第 $i$ 行」元素旋转到「第 $n - 1 - i$ 列」元素; |
6 | | -- 「第 $j$ 列」元素旋转到「第 $j$ 行」元素; |
7 | | - |
8 | | -因此,对于矩阵任意第 $i$ 行、第 $j$ 列元素 $matrix[i][j]$ ,矩阵旋转 90º 后「元素位置旋转公式」为: |
| 5 | +若只向窗口 $[i, j]$ 右边添加数字 $nums[j + 1]$ ,则新窗口最大值可以 **通过一次对比** 使用 $O(1)$ 时间得到,即: |
9 | 6 |
|
10 | 7 | $$ |
11 | | -\begin{aligned} |
12 | | -matrix[i][j] & \rightarrow matrix[j][n - 1 - i] \\ |
13 | | -原索引位置 & \rightarrow 旋转后索引位置 |
14 | | -\end{aligned} |
| 8 | +x_{j+1} = \max(x_{j}, nums[j + 1]) |
15 | 9 | $$ |
16 | 10 |
|
17 | | - |
18 | | - |
19 | | -根据以上「元素旋转公式」,考虑遍历矩阵,将各元素依次写入到旋转后的索引位置。但仍**存在问题**:在写入一个元素 $matrix[i][j] \rightarrow matrix[j][n - 1 - i]$ 后,原矩阵元素 $matrix[j][n - 1 - i]$ 就会**被覆盖(即丢失)**,而此丢失的元素就无法被写入到旋转后的索引位置了。 |
20 | | - |
21 | | -为解决此问题,考虑借助一个「辅助矩阵」暂存原矩阵,通过遍历辅助矩阵所有元素,将各元素填入「原矩阵」旋转后的新索引位置即可。 |
22 | | - |
23 | | -```Python [] |
24 | | -class Solution: |
25 | | - def rotate(self, matrix: List[List[int]]) -> None: |
26 | | - n = len(matrix) |
27 | | - # 深拷贝 matrix -> tmp |
28 | | - tmp = copy.deepcopy(matrix) |
29 | | - # 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素 |
30 | | - for i in range(n): |
31 | | - for j in range(n): |
32 | | - matrix[j][n - 1 - i] = tmp[i][j] |
33 | | -``` |
34 | | - |
35 | | -```Java [] |
36 | | -class Solution { |
37 | | - public void rotate(int[][] matrix) { |
38 | | - int n = matrix.length; |
39 | | - // 深拷贝 matrix -> tmp |
40 | | - int[][] tmp = new int[n][]; |
41 | | - for (int i = 0; i < n; i++) |
42 | | - tmp[i] = matrix[i].clone(); |
43 | | - // 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素 |
44 | | - for (int i = 0; i < n; i++) { |
45 | | - for (int j = 0; j < n; j++) { |
46 | | - matrix[j][n - 1 - i] = tmp[i][j]; |
47 | | - } |
48 | | - } |
49 | | - } |
50 | | -} |
51 | | -``` |
52 | | - |
53 | | -```C++ [] |
54 | | -class Solution { |
55 | | -public: |
56 | | - void rotate(vector<vector<int>>& matrix) { |
57 | | - int n = matrix.size(); |
58 | | - // 深拷贝 matrix -> tmp |
59 | | - vector<vector<int>> tmp = matrix; |
60 | | - // 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素 |
61 | | - for (int i = 0; i < n; i++) { |
62 | | - for (int j = 0; j < n; j++) { |
63 | | - matrix[j][n - 1 - i] = tmp[i][j]; |
64 | | - } |
65 | | - } |
66 | | - } |
67 | | -}; |
68 | | -``` |
69 | | -
|
70 | | -如以上代码所示,遍历矩阵所有元素的时间复杂度为 $O(N^2)$ ;由于借助了一个辅助矩阵,**空间复杂度**为 $O(N^2)$ 。 |
71 | | -
|
72 | | -# 方法二:原地修改 |
73 | | -
|
74 | | -考虑不借助辅助矩阵,通过在原矩阵中直接「原地修改」,实现空间复杂度 $O(1)$ 的解法。 |
75 | | -
|
76 | | -以位于矩阵四个角点的元素为例,设矩阵左上角元素 $A$ 、右上角元素 $B$ 、右下角元素 $C$ 、左下角元素 $D$ 。矩阵旋转 90º 后,相当于依次先后执行 $D \rightarrow A$ , $C \rightarrow D$ , $B \rightarrow C$ , $A \rightarrow B$ 修改元素,即如下「首尾相接」的元素旋转操作: |
| 11 | +而由于删除的 $nums[i]$ 可能恰好是窗口内唯一的最大值 $x_j$ ,因此不能通过以上方法计算 $x_{j+1}$ ,而必须使用 $O(j-i)$ 时间, **遍历整个窗口区间** 获取最大值,即: |
77 | 12 |
|
78 | 13 | $$ |
79 | | -A \leftarrow D \leftarrow C \leftarrow B \leftarrow A |
| 14 | +x_{j+1} = \max(nums(i+1), \cdots , num(j+1)) |
80 | 15 | $$ |
81 | 16 |
|
82 | | -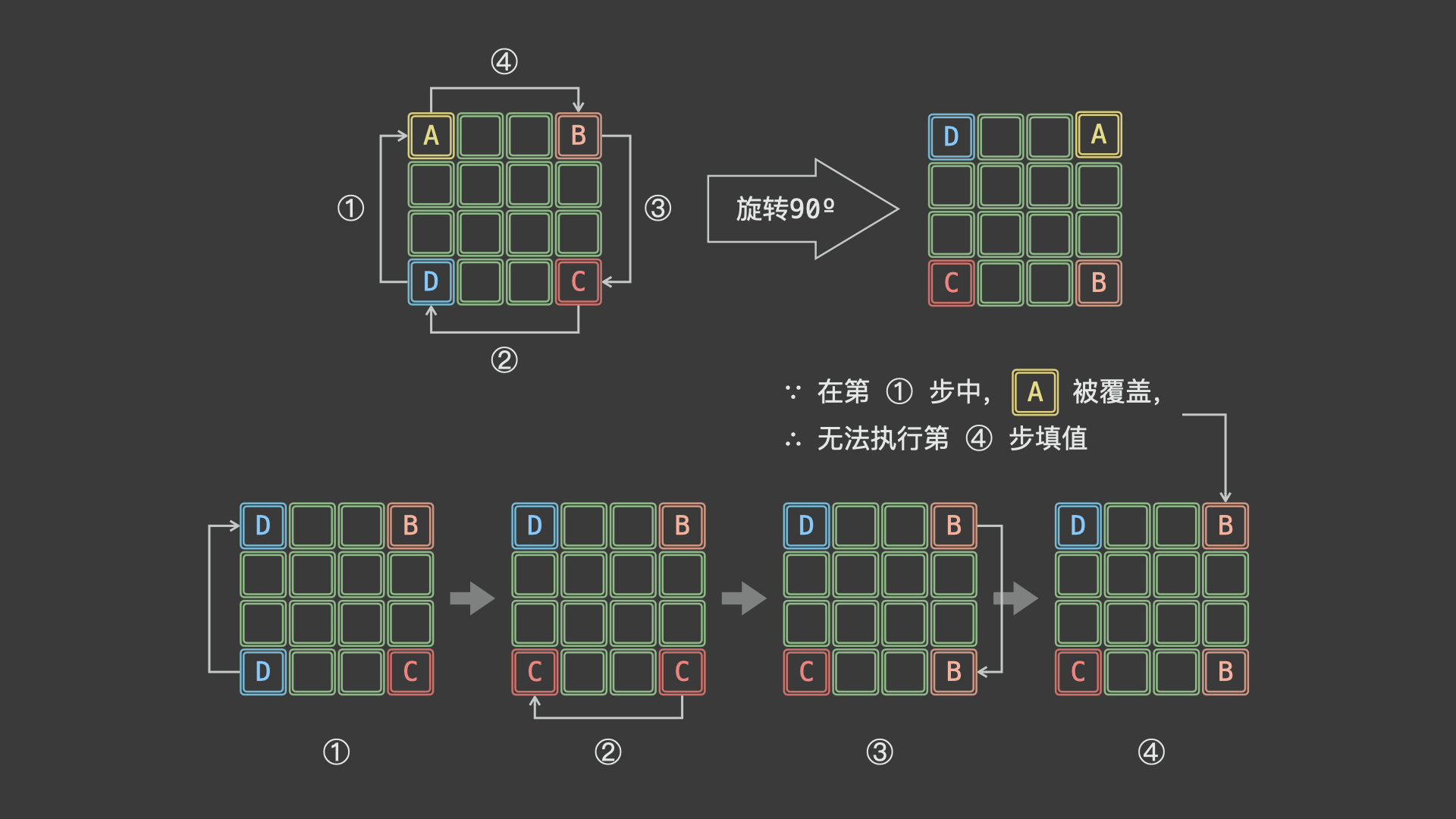 |
| 17 | +根据以上分析,可得 **暴力法** 的时间复杂度为 $O((n-k+1)k) \approx O(nk)$ 。 |
83 | 18 |
|
84 | | -如上图所示,由于第 $1$ 步 $D \rightarrow A$ 已经将 $A$ 覆盖(导致 $A$ 丢失),此丢失导致最后第 $4$ 步 $A \rightarrow B$ 无法赋值。为解决此问题,考虑借助一个「辅助变量 $tmp$ 」预先存储 $A$ ,此时的旋转操作变为: |
| 19 | +- 设数组 $nums$ 的长度为 $n$ ,则共有 $(n-k+1)$ 个窗口; |
| 20 | +- 获取每个窗口最大值需线性遍历,时间复杂度为 $O(k)$ 。 |
85 | 21 |
|
86 | | -$$ |
87 | | -暂存 \ tmp = A \\ |
88 | | -A \leftarrow D \leftarrow C \leftarrow B \leftarrow tmp |
89 | | -$$ |
| 22 | +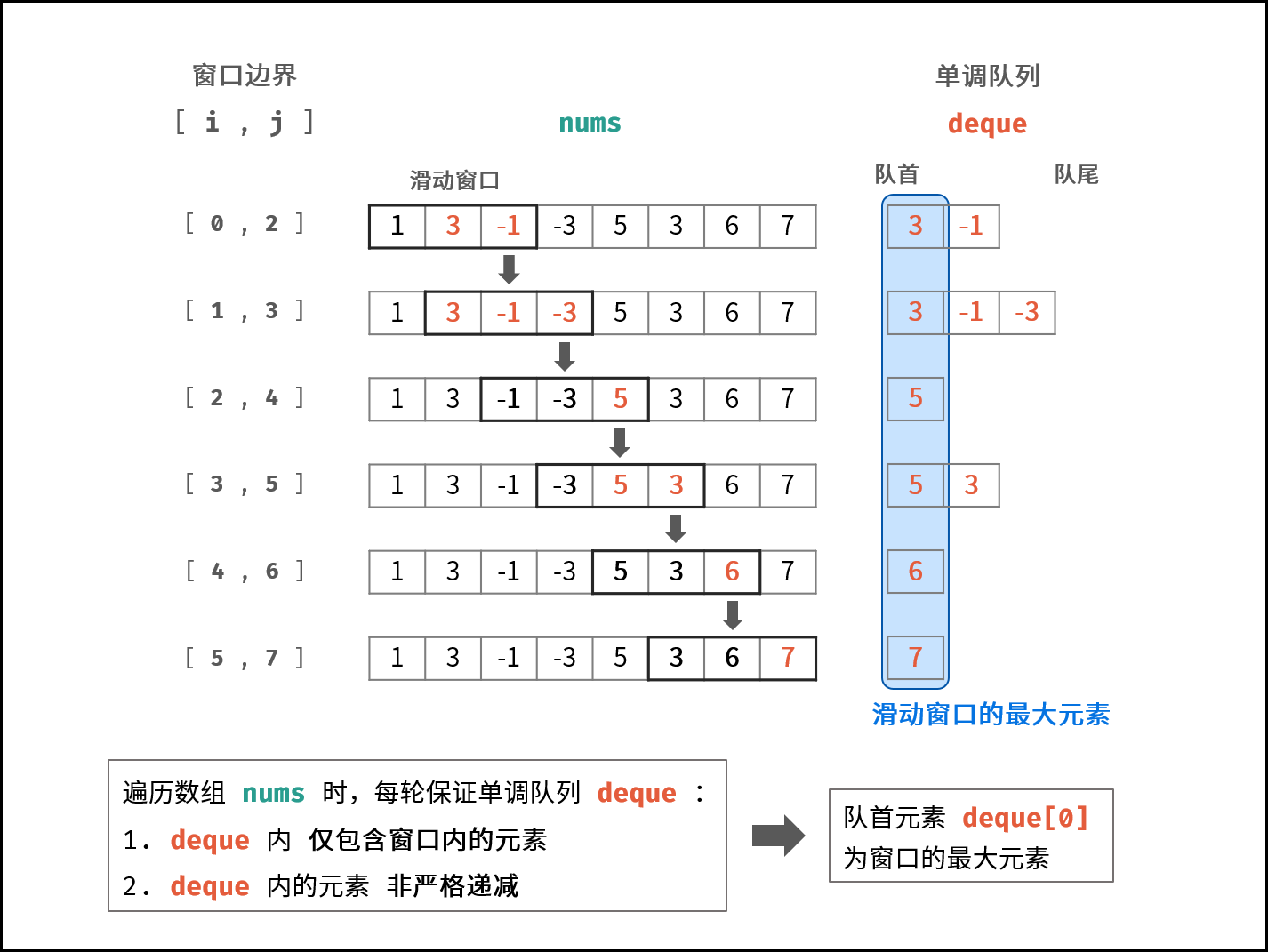{:width=650} |
90 | 23 |
|
91 | | -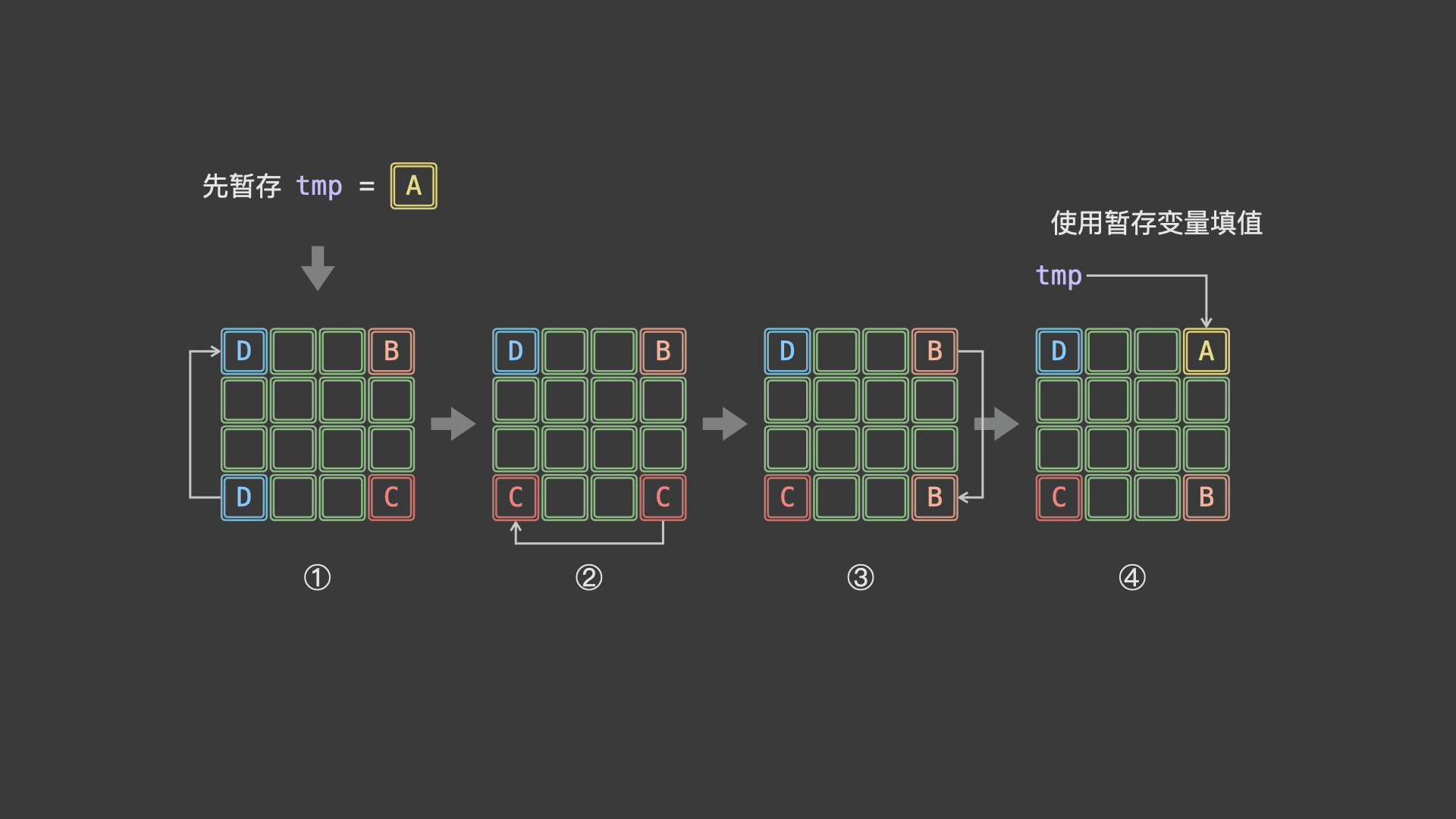 |
| 24 | +> **本题难点:** 如何在每次窗口滑动后,将 “获取窗口内最大值” 的时间复杂度从 $O(k)$ 降低至 $O(1)$ 。 |
92 | 25 |
|
93 | | -如上图所示,一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 $1/4$ 的各元素为起始点执行以上旋转操作,即可完整实现矩阵旋转。 |
| 26 | +回忆 [最小栈](https://leetcode.cn/problems/min-stack/) ,其使用 **单调栈** 实现了随意入栈、出栈情况下的 $O(1)$ 时间获取 “栈内最小值” 。本题同理,不同点在于 “出栈操作” 删除的是 “列表尾部元素” ,而 “窗口滑动” 删除的是 “列表首部元素” 。 |
94 | 27 |
|
95 | | -具体来看,当矩阵大小 $n$ 为偶数时,取前 $\frac{n}{2}$ 行、前 $\frac{n}{2}$ 列的元素为起始点;当矩阵大小 $n$ 为奇数时,取前 $\frac{n}{2}$ 行、前 $\frac{n + 1}{2}$ 列的元素为起始点。 |
| 28 | +窗口对应的数据结构为 **双端队列** ,本题使用 **单调队列** 即可解决以上问题。遍历数组时,每轮保证单调队列 $deque$ : |
96 | 29 |
|
97 | | -令 $matrix[i][j] = A$ ,根据文章开头的元素旋转公式,可推导得适用于任意起始点的元素旋转操作: |
| 30 | +1. $deque$ 内 **仅包含窗口内的元素** $\Rightarrow$ 每轮窗口滑动移除了元素 $nums[i - 1]$ ,需将 $deque$ 内的对应元素一起删除。 |
| 31 | +2. $deque$ 内的元素 **非严格递减** $\Rightarrow$ 每轮窗口滑动添加了元素 $nums[j + 1]$ ,需将 $deque$ 内所有 $< nums[j + 1]$ 的元素删除。 |
98 | 32 |
|
99 | | -$$ |
100 | | -暂存 tmp = matrix[i][j] \\ |
101 | | -matrix[i][j] \leftarrow matrix[n - 1 - j][i] \leftarrow matrix[n - 1 - i][n - 1 - j] \leftarrow matrix[j][n - 1 - i] \leftarrow tmp |
102 | | -$$ |
| 33 | +### 算法流程: |
103 | 34 |
|
104 | | -> 如下图所示,为示例矩阵的算法执行流程。 |
| 35 | +1. **初始化:** 双端队列 $deque$ ,结果列表 $res$ ,数组长度 $n$ ; |
| 36 | +2. **滑动窗口:** 左边界范围 $i \in [1 - k, n - k]$ ,右边界范围 $j \in [0, n - 1]$ ; |
| 37 | + 1. 若 $i > 0$ 且 队首元素 $deque[0]$ $=$ 被删除元素 $nums[i - 1]$ :则队首元素出队; |
| 38 | + 2. 删除 $deque$ 内所有 $< nums[j]$ 的元素,以保持 $deque$ 递减; |
| 39 | + 3. 将 $nums[j]$ 添加至 $deque$ 尾部; |
| 40 | + 4. 若已形成窗口(即 $i \geq 0$ ):将窗口最大值(即队首元素 $deque[0]$ )添加至列表 $res$ ; |
| 41 | +3. **返回值:** 返回结果列表 $res$ ; |
105 | 42 |
|
106 | | -<,,,,,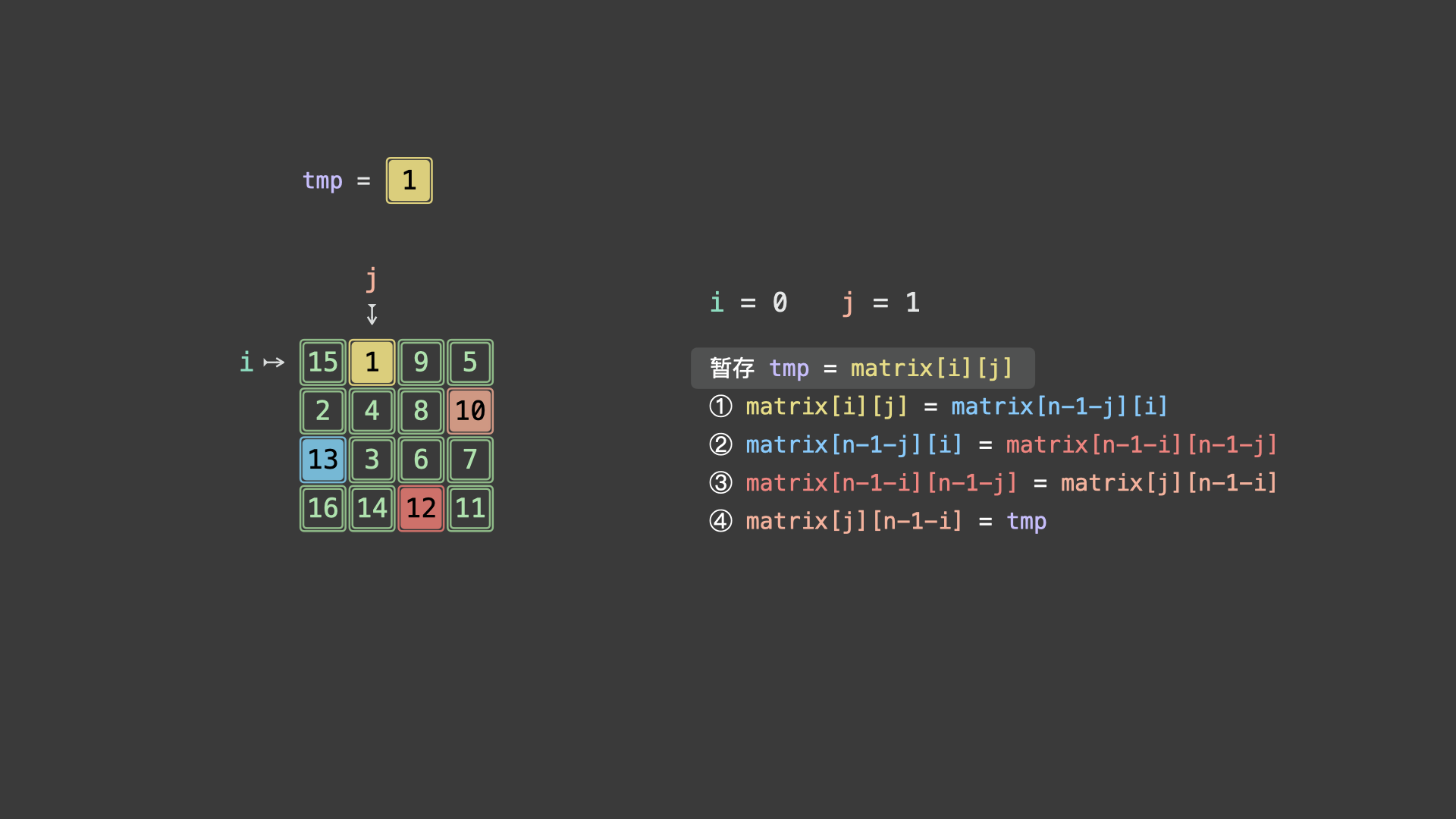,,,,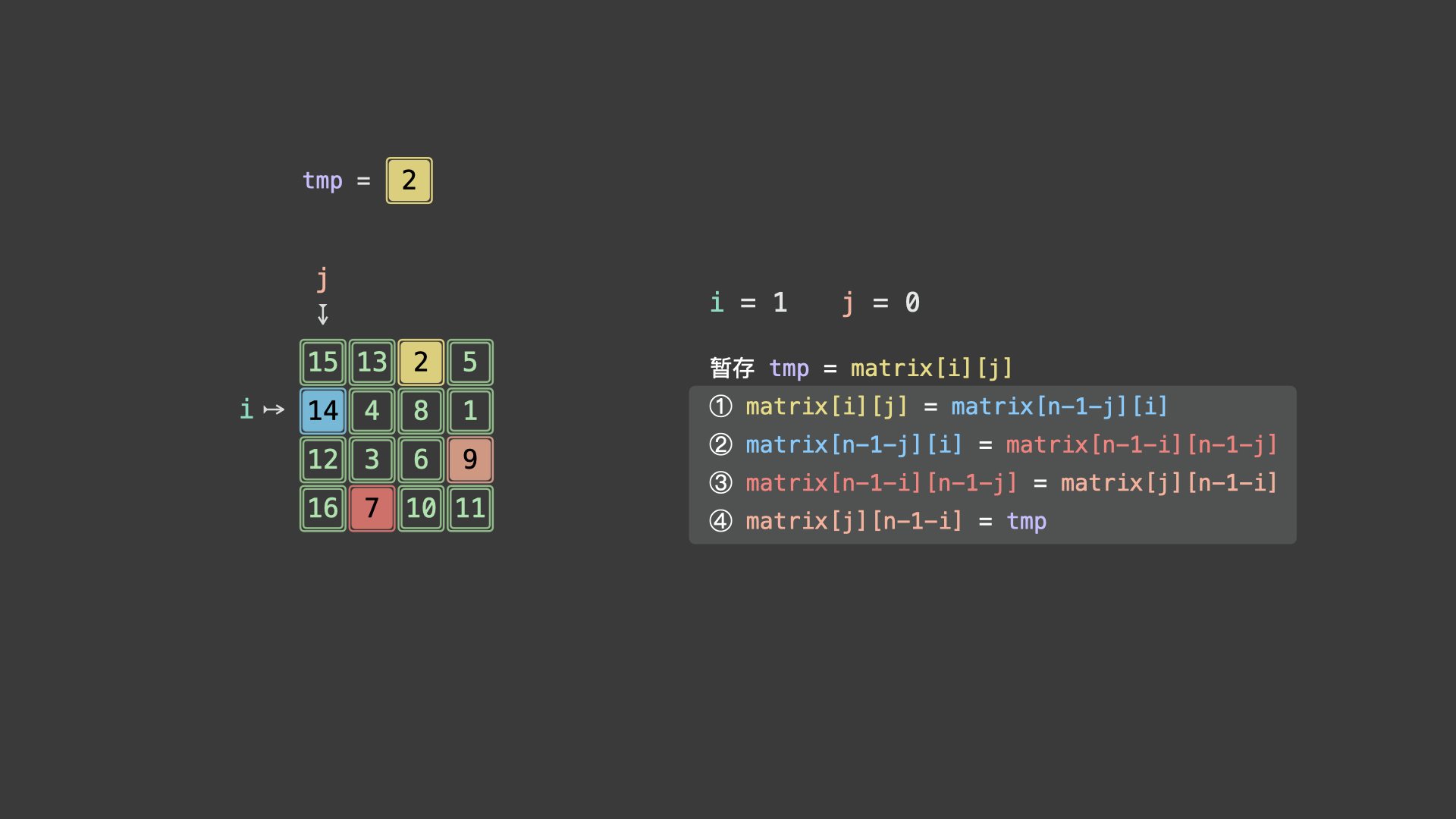,,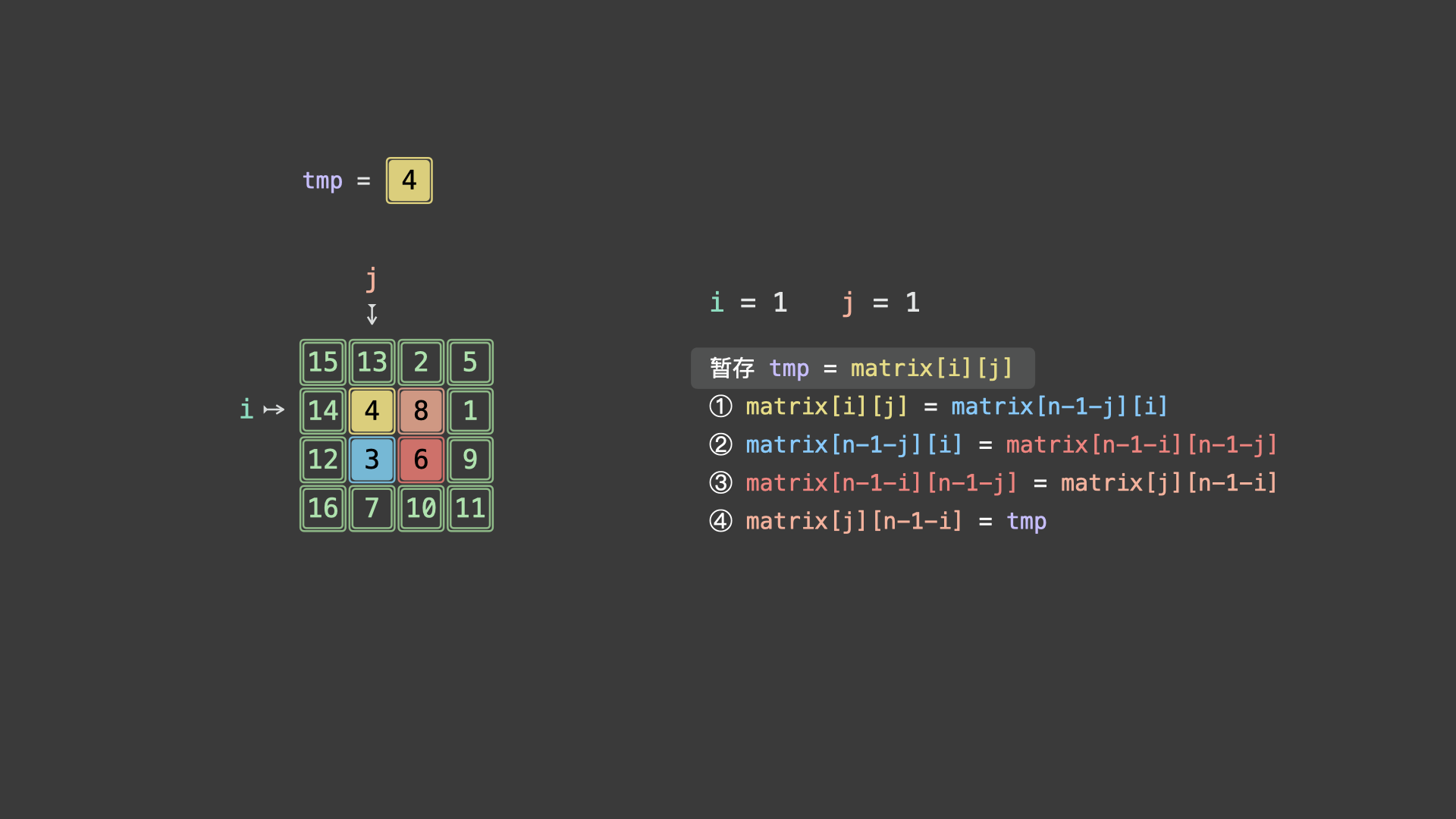,,> |
| 43 | +<,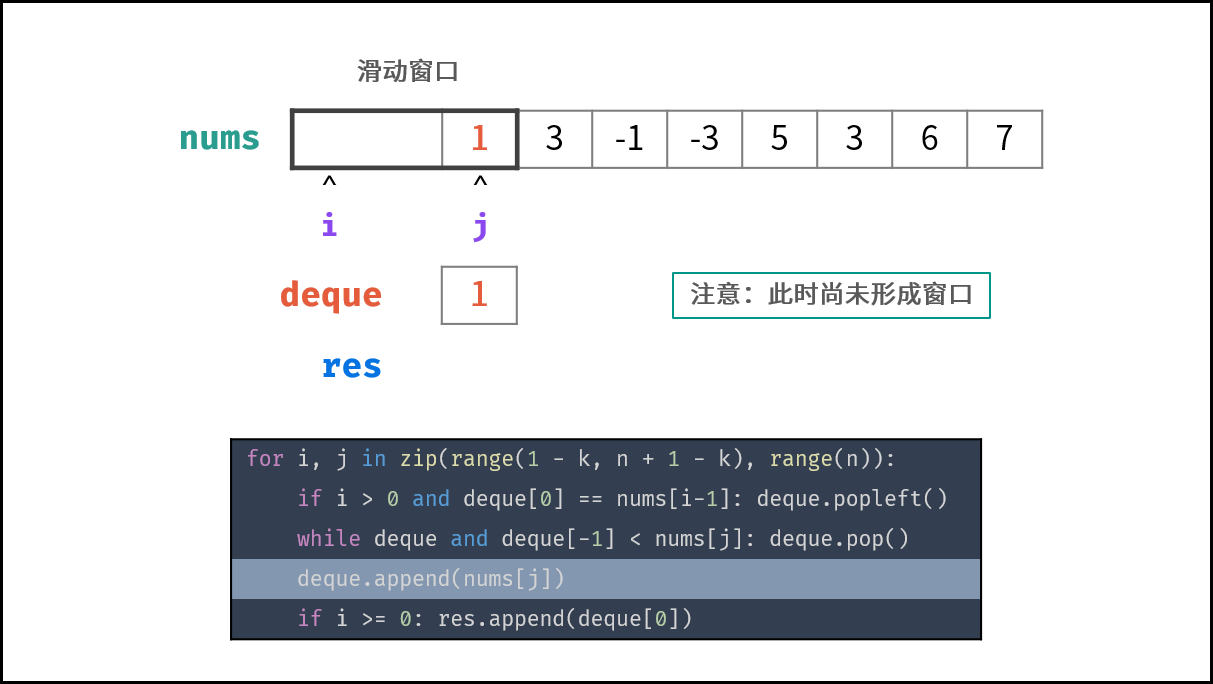,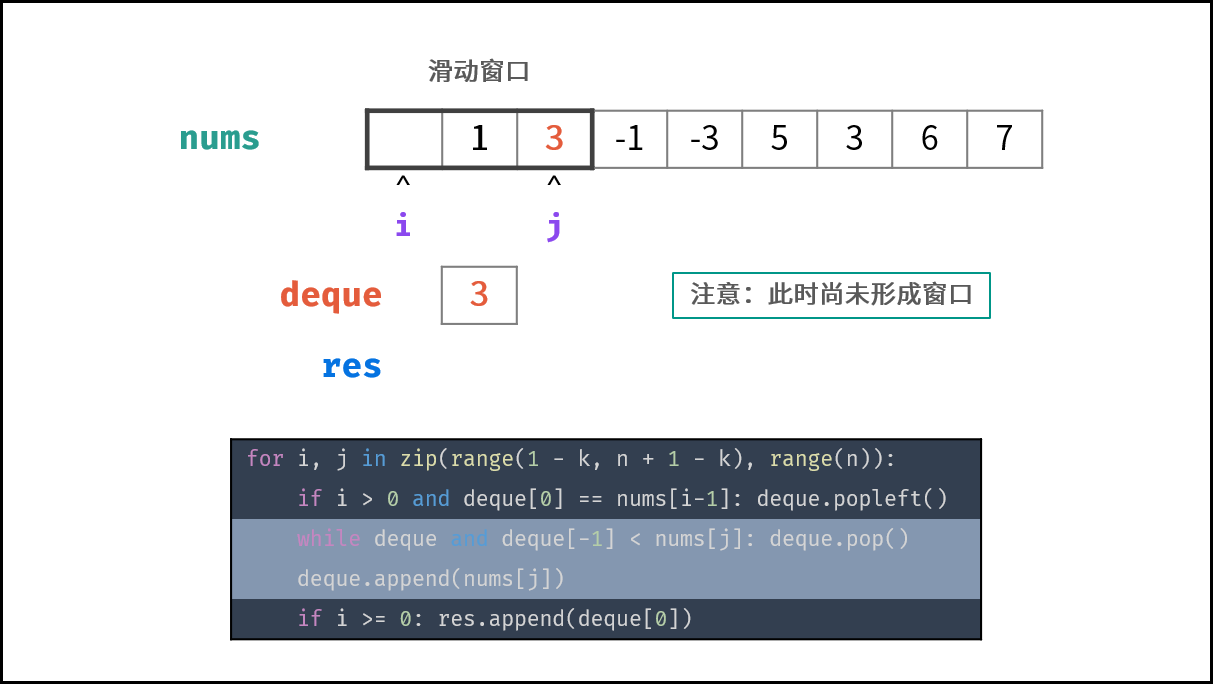,,,,,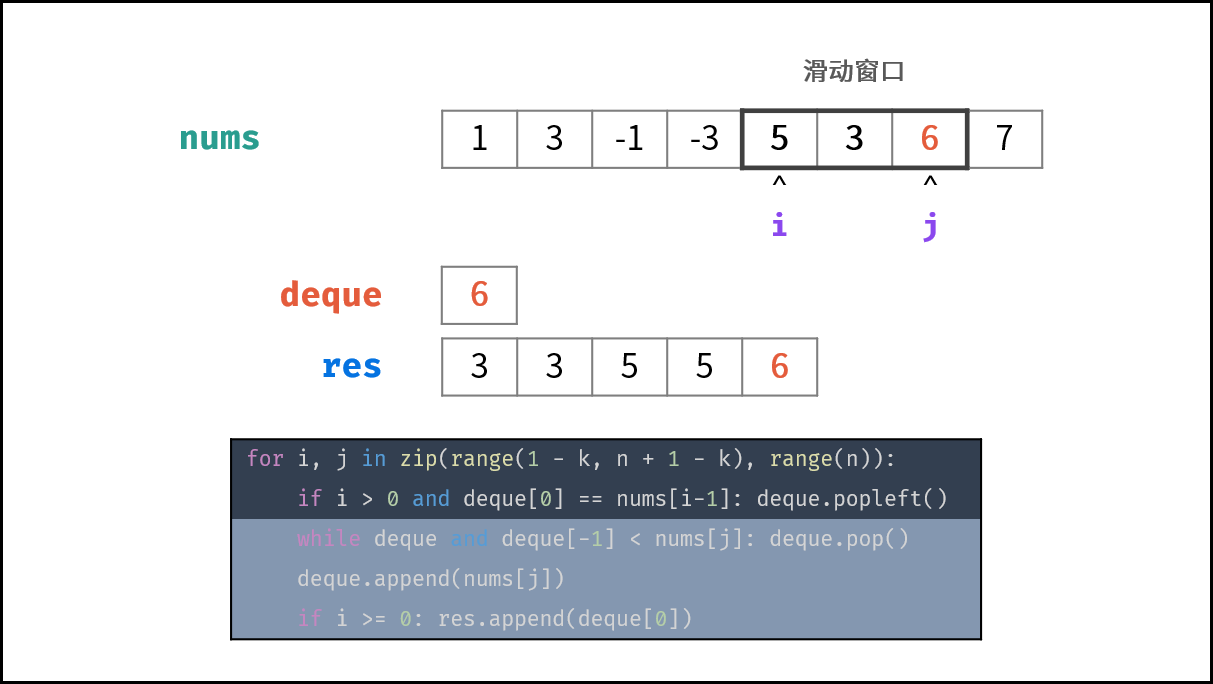,,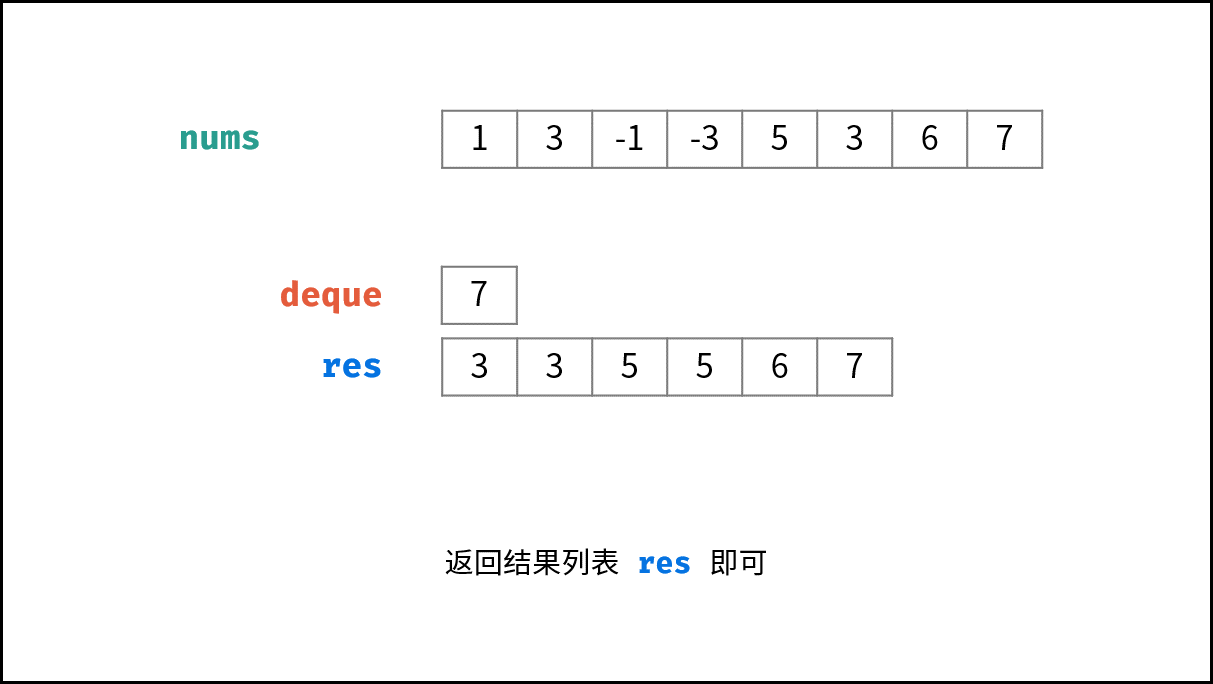> |
107 | 44 |
|
108 | | -## 代码 |
| 45 | +## 代码: |
109 | 46 |
|
110 | | -> 后三个 Tab 为「代码注释解析」。 |
| 47 | +Python 通过 `zip(range(), range())` 可实现滑动窗口的左右边界 `i, j` 同时遍历。 |
111 | 48 |
|
112 | 49 | ```Python [] |
113 | 50 | class Solution: |
114 | | - def rotate(self, matrix: List[List[int]]) -> None: |
115 | | - n = len(matrix) |
116 | | - for i in range(n // 2): |
117 | | - for j in range((n + 1) // 2): |
118 | | - tmp = matrix[i][j] |
119 | | - matrix[i][j] = matrix[n - 1 - j][i] |
120 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j] |
121 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i] |
122 | | - matrix[j][n - 1 - i] = tmp |
| 51 | + def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]: |
| 52 | + deque = collections.deque() |
| 53 | + res, n = [], len(nums) |
| 54 | + for i, j in zip(range(1 - k, n + 1 - k), range(n)): |
| 55 | + # 删除 deque 中对应的 nums[i-1] |
| 56 | + if i > 0 and deque[0] == nums[i - 1]: |
| 57 | + deque.popleft() |
| 58 | + # 保持 deque 递减 |
| 59 | + while deque and deque[-1] < nums[j]: |
| 60 | + deque.pop() |
| 61 | + deque.append(nums[j]) |
| 62 | + # 记录窗口最大值 |
| 63 | + if i >= 0: |
| 64 | + res.append(deque[0]) |
| 65 | + return res |
123 | 66 | ``` |
124 | 67 |
|
125 | 68 | ```Java [] |
126 | 69 | class Solution { |
127 | | - public void rotate(int[][] matrix) { |
128 | | - int n = matrix.length; |
129 | | - for (int i = 0; i < n / 2; i++) { |
130 | | - for (int j = 0; j < (n + 1) / 2; j++) { |
131 | | - int tmp = matrix[i][j]; |
132 | | - matrix[i][j] = matrix[n - 1 - j][i]; |
133 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]; |
134 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]; |
135 | | - matrix[j][n - 1 - i] = tmp; |
136 | | - } |
| 70 | + public int[] maxSlidingWindow(int[] nums, int k) { |
| 71 | + if(nums.length == 0 || k == 0) return new int[0]; |
| 72 | + Deque<Integer> deque = new LinkedList<>(); |
| 73 | + int[] res = new int[nums.length - k + 1]; |
| 74 | + for(int j = 0, i = 1 - k; j < nums.length; i++, j++) { |
| 75 | + // 删除 deque 中对应的 nums[i-1] |
| 76 | + if(i > 0 && deque.peekFirst() == nums[i - 1]) |
| 77 | + deque.removeFirst(); |
| 78 | + // 保持 deque 递减 |
| 79 | + while(!deque.isEmpty() && deque.peekLast() < nums[j]) |
| 80 | + deque.removeLast(); |
| 81 | + deque.addLast(nums[j]); |
| 82 | + // 记录窗口最大值 |
| 83 | + if(i >= 0) |
| 84 | + res[i] = deque.peekFirst(); |
137 | 85 | } |
| 86 | + return res; |
138 | 87 | } |
139 | 88 | } |
140 | 89 | ``` |
141 | 90 |
|
142 | 91 | ```C++ [] |
143 | 92 | class Solution { |
144 | 93 | public: |
145 | | - void rotate(vector<vector<int>>& matrix) { |
146 | | - int n = matrix.size(); |
147 | | - for (int i = 0; i < n / 2; i++) { |
148 | | - for (int j = 0; j < (n + 1) / 2; j++) { |
149 | | - int tmp = matrix[i][j]; |
150 | | - matrix[i][j] = matrix[n - 1 - j][i]; |
151 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]; |
152 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]; |
153 | | - matrix[j][n - 1 - i] = tmp; |
154 | | - } |
| 94 | + vector<int> maxSlidingWindow(vector<int>& nums, int k) { |
| 95 | + if(nums.size() == 0 || k == 0) return {}; |
| 96 | + deque<int> deque; |
| 97 | + vector<int> res(nums.size() - k + 1); |
| 98 | + for(int j = 0, i = 1 - k; j < nums.size(); i++, j++) { |
| 99 | + // 删除 deque 中对应的 nums[i-1] |
| 100 | + if(i > 0 && deque.front() == nums[i - 1]) |
| 101 | + deque.pop_front(); |
| 102 | + // 保持 deque 递减 |
| 103 | + while(!deque.empty() && deque.back() < nums[j]) |
| 104 | + deque.pop_back(); |
| 105 | + deque.push_back(nums[j]); |
| 106 | + // 记录窗口最大值 |
| 107 | + if(i >= 0) |
| 108 | + res[i] = deque.front(); |
155 | 109 | } |
| 110 | + return res; |
| 111 | + } |
156 | 112 | } |
157 | 113 | }; |
158 | 114 | ``` |
159 | 115 |
|
| 116 | +可以将 “未形成窗口” 和 “形成窗口后” 两个阶段拆分到两个循环里实现。代码虽变长,但减少了冗余的判断操作。 |
| 117 | +
|
160 | 118 | ```Python [] |
161 | 119 | class Solution: |
162 | | - def rotate(self, matrix: List[List[int]]) -> None: |
163 | | - # 设矩阵行列数为 n |
164 | | - n = len(matrix) |
165 | | - # 起始点范围为 0 <= i < n // 2 , 0 <= j < (n + 1) // 2 |
166 | | - # 其中 '//' 为整数除法 |
167 | | - for i in range(n // 2): |
168 | | - for j in range((n + 1) // 2): |
169 | | - # 暂存 A 至 tmp |
170 | | - tmp = matrix[i][j] |
171 | | - # 元素旋转操作 A <- D <- C <- B <- tmp |
172 | | - matrix[i][j] = matrix[n - 1 - j][i] |
173 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j] |
174 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i] |
175 | | - matrix[j][n - 1 - i] = tmp |
| 120 | + def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]: |
| 121 | + if not nums or k == 0: return [] |
| 122 | + deque = collections.deque() |
| 123 | + # 未形成窗口 |
| 124 | + for i in range(k): |
| 125 | + while deque and deque[-1] < nums[i]: |
| 126 | + deque.pop() |
| 127 | + deque.append(nums[i]) |
| 128 | + res = [deque[0]] |
| 129 | + # 形成窗口后 |
| 130 | + for i in range(k, len(nums)): |
| 131 | + if deque[0] == nums[i - k]: |
| 132 | + deque.popleft() |
| 133 | + while deque and deque[-1] < nums[i]: |
| 134 | + deque.pop() |
| 135 | + deque.append(nums[i]) |
| 136 | + res.append(deque[0]) |
| 137 | + return res |
176 | 138 | ``` |
177 | 139 |
|
178 | 140 | ```Java [] |
179 | 141 | class Solution { |
180 | | - public void rotate(int[][] matrix) { |
181 | | - // 设矩阵行列数为 n |
182 | | - int n = matrix.length; |
183 | | - // 起始点范围为 0 <= i < n / 2 , 0 <= j < (n + 1) / 2 |
184 | | - // 其中 '/' 为整数除法 |
185 | | - for (int i = 0; i < n / 2; i++) { |
186 | | - for (int j = 0; j < (n + 1) / 2; j++) { |
187 | | - // 暂存 A 至 tmp |
188 | | - int tmp = matrix[i][j]; |
189 | | - // 元素旋转操作 A <- D <- C <- B <- tmp |
190 | | - matrix[i][j] = matrix[n - 1 - j][i]; |
191 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]; |
192 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]; |
193 | | - matrix[j][n - 1 - i] = tmp; |
194 | | - } |
| 142 | + public int[] maxSlidingWindow(int[] nums, int k) { |
| 143 | + if(nums.length == 0 || k == 0) return new int[0]; |
| 144 | + Deque<Integer> deque = new LinkedList<>(); |
| 145 | + int[] res = new int[nums.length - k + 1]; |
| 146 | + // 未形成窗口 |
| 147 | + for(int i = 0; i < k; i++) { |
| 148 | + while(!deque.isEmpty() && deque.peekLast() < nums[i]) |
| 149 | + deque.removeLast(); |
| 150 | + deque.addLast(nums[i]); |
195 | 151 | } |
| 152 | + res[0] = deque.peekFirst(); |
| 153 | + // 形成窗口后 |
| 154 | + for(int i = k; i < nums.length; i++) { |
| 155 | + if(deque.peekFirst() == nums[i - k]) |
| 156 | + deque.removeFirst(); |
| 157 | + while(!deque.isEmpty() && deque.peekLast() < nums[i]) |
| 158 | + deque.removeLast(); |
| 159 | + deque.addLast(nums[i]); |
| 160 | + res[i - k + 1] = deque.peekFirst(); |
| 161 | + } |
| 162 | + return res; |
196 | 163 | } |
197 | 164 | } |
198 | 165 | ``` |
199 | 166 |
|
200 | 167 | ```C++ [] |
201 | 168 | class Solution { |
202 | 169 | public: |
203 | | - void rotate(vector<vector<int>>& matrix) { |
204 | | - // 设矩阵行列数为 n |
205 | | - int n = matrix.size(); |
206 | | - // 起始点范围为 0 <= i < n / 2 , 0 <= j < (n + 1) / 2 |
207 | | - // 其中 '/' 为整数除法 |
208 | | - for (int i = 0; i < n / 2; i++) { |
209 | | - for (int j = 0; j < (n + 1) / 2; j++) { |
210 | | - // 暂存 A 至 tmp |
211 | | - int tmp = matrix[i][j]; |
212 | | - // 元素旋转操作 A <- D <- C <- B <- tmp |
213 | | - matrix[i][j] = matrix[n - 1 - j][i]; |
214 | | - matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]; |
215 | | - matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]; |
216 | | - matrix[j][n - 1 - i] = tmp; |
217 | | - } |
| 170 | + vector<int> maxSlidingWindow(vector<int>& nums, int k) { |
| 171 | + if(nums.size() == 0 || k == 0) return {}; |
| 172 | + deque<int> deque; |
| 173 | + vector<int> res(nums.size() - k + 1); |
| 174 | + // 未形成窗口 |
| 175 | + for(int i = 0; i < k; i++) { |
| 176 | + while(!deque.empty() && deque.back() < nums[i]) |
| 177 | + deque.pop_back(); |
| 178 | + deque.push_back(nums[i]); |
| 179 | + } |
| 180 | + res[0] = deque.front(); |
| 181 | + // 形成窗口后 |
| 182 | + for(int i = k; i < nums.size(); i++) { |
| 183 | + if(deque.front() == nums[i - k]) |
| 184 | + deque.pop_front(); |
| 185 | + while(!deque.empty() && deque.back() < nums[i]) |
| 186 | + deque.pop_back(); |
| 187 | + deque.push_back(nums[i]); |
| 188 | + res[i - k + 1] = deque.front(); |
218 | 189 | } |
| 190 | + return res; |
219 | 191 | } |
220 | 192 | }; |
221 | 193 | ``` |
222 | 194 |
|
223 | | -## 复杂度分析 |
| 195 | +### 复杂度分析: |
224 | 196 |
|
225 | | -- **时间复杂度 $O(N^2)$ :** 其中 $N$ 为输入矩阵的行(列)数。需要将矩阵中每个元素旋转到新的位置,即对矩阵所有元素操作一次,使用 $O(N^2)$ 时间。 |
226 | | -- **空间复杂度 $O(1)$ :** 临时变量 $tmp$ 使用常数大小的额外空间。值得注意,当循环中进入下轮迭代,上轮迭代初始化的 $tmp$ 占用的内存就会被自动释放,因此无累计使用空间。 |
| 197 | +- **时间复杂度 $O(n)$ :** 其中 $n$ 为数组 $nums$ 长度;线性遍历 $nums$ 占用 $O(n)$ ;每个元素最多仅入队和出队一次,因此单调队列 $deque$ 占用 $O(2n)$ 。 |
| 198 | +- **空间复杂度 $O(k)$ :** 双端队列 $deque$ 中最多同时存储 $k$ 个元素(即窗口大小)。 |
0 commit comments