|
| 1 | +# Red–Black Tree |
| 2 | + |
| 3 | +A red–black tree is a kind of self-balancing binary search |
| 4 | +tree in computer science. Each node of the binary tree has |
| 5 | +an extra bit, and that bit is often interpreted as the |
| 6 | +color (red or black) of the node. These color bits are used |
| 7 | +to ensure the tree remains approximately balanced during |
| 8 | +insertions and deletions. |
| 9 | + |
| 10 | +Balance is preserved by painting each node of the tree with |
| 11 | +one of two colors in a way that satisfies certain properties, |
| 12 | +which collectively constrain how unbalanced the tree can |
| 13 | +become in the worst case. When the tree is modified, the |
| 14 | +new tree is subsequently rearranged and repainted to |
| 15 | +restore the coloring properties. The properties are |
| 16 | +designed in such a way that this rearranging and recoloring |
| 17 | +can be performed efficiently. |
| 18 | + |
| 19 | +The balancing of the tree is not perfect, but it is good |
| 20 | +enough to allow it to guarantee searching in `O(log n)` time, |
| 21 | +where `n` is the total number of elements in the tree. |
| 22 | +The insertion and deletion operations, along with the tree |
| 23 | +rearrangement and recoloring, are also performed |
| 24 | +in `O(log n)` time. |
| 25 | + |
| 26 | +An example of a red–black tree: |
| 27 | + |
| 28 | + |
| 29 | + |
| 30 | +## Properties |
| 31 | + |
| 32 | +In addition to the requirements imposed on a binary search |
| 33 | +tree the following must be satisfied by a red–black tree: |
| 34 | + |
| 35 | +- Each node is either red or black. |
| 36 | +- The root is black. This rule is sometimes omitted. |
| 37 | +Since the root can always be changed from red to black, |
| 38 | +but not necessarily vice versa, this rule has little |
| 39 | +effect on analysis. |
| 40 | +- All leaves (NIL) are black. |
| 41 | +- If a node is red, then both its children are black. |
| 42 | +- Every path from a given node to any of its descendant |
| 43 | +NIL nodes contains the same number of black nodes. |
| 44 | + |
| 45 | +Some definitions: the number of black nodes from the root |
| 46 | +to a node is the node's **black depth**; the uniform |
| 47 | +number of black nodes in all paths from root to the leaves |
| 48 | +is called the **black-height** of the red–black tree. |
| 49 | + |
| 50 | +These constraints enforce a critical property of red–black |
| 51 | +trees: _the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf_. |
| 52 | +The result is that the tree is roughly height-balanced. |
| 53 | +Since operations such as inserting, deleting, and finding |
| 54 | +values require worst-case time proportional to the height |
| 55 | +of the tree, this theoretical upper bound on the height |
| 56 | +allows red–black trees to be efficient in the worst case, |
| 57 | +unlike ordinary binary search trees. |
| 58 | + |
| 59 | +## Balancing during insertion |
| 60 | + |
| 61 | +### If uncle is RED |
| 62 | +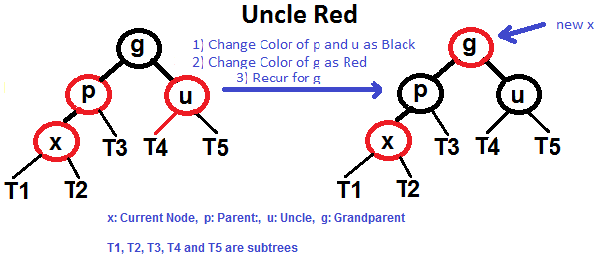 |
| 63 | + |
| 64 | +### If uncle is BLACK |
| 65 | + |
| 66 | +- Left Left Case (`p` is left child of `g` and `x` is left child of `p`) |
| 67 | +- Left Right Case (`p` is left child of `g` and `x` is right child of `p`) |
| 68 | +- Right Right Case (`p` is right child of `g` and `x` is right child of `p`) |
| 69 | +- Right Left Case (`p` is right child of `g` and `x` is left child of `p`) |
| 70 | + |
| 71 | +#### Left Left Case (See g, p and x) |
| 72 | + |
| 73 | +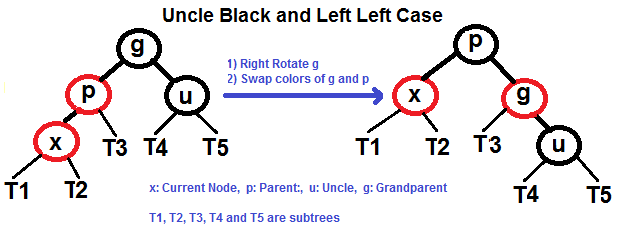 |
| 74 | + |
| 75 | +#### Left Right Case (See g, p and x) |
| 76 | + |
| 77 | +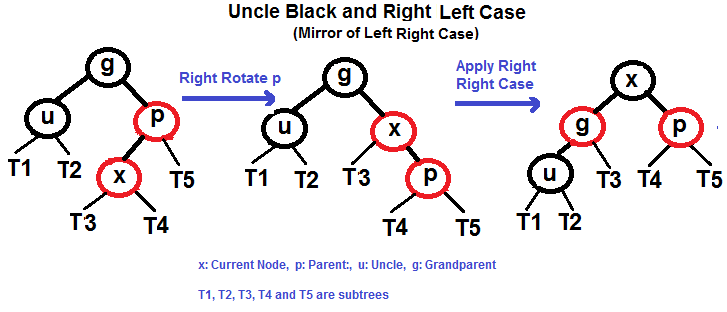 |
| 78 | + |
| 79 | +#### Right Right Case (See g, p and x) |
| 80 | + |
| 81 | +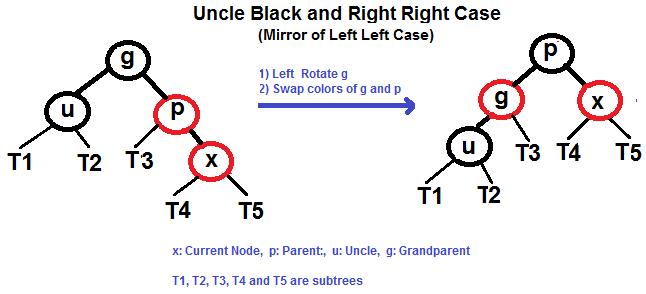 |
| 82 | + |
| 83 | +#### Right Left Case (See g, p and x) |
| 84 | + |
| 85 | + |
| 86 | + |
| 87 | +## References |
| 88 | + |
| 89 | +- [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree) |
| 90 | +- [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63) |
| 91 | +- [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64) |
| 92 | +- [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/) |
| 93 | +- [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html) |
0 commit comments