添加了基础排序算法和二叉树的遍历

hicf · hicf · commit c171854b46bb · 2019-06-11T18:06:29.000+08:00
diff --git a/README.md b/README.md
@@ -4,7 +4,16 @@
 
 ### :lollipop::lollipop::lollipop:全文持续更新中 ... :recycle::recycle::recycle:
 
+
+
+### 零、:rocket::rocket::rocket:数据结构与算法
+
+* [数据结构与算法 （第 01 篇） Java版：常见基础排序算法与复杂度](https://github.com/about-cloud/JavaCore/blob/master/resource/markdown/algorithm/BasicSorting.md)
+* [数据结构与算法 （第 02 篇） Java版：二叉树遍历的n种方法](https://github.com/about-cloud/JavaCore/blob/master/resource/markdown/algorithm/BinaryTreeTraversal.md)
+
+
 ### 一、:bullettrain_side::railway_car::railway_car::railway_car:集合框架源码分析
+
 * [集合框架 （第 01 篇） 源码分析：Collection<E> 框架总览](https://github.com/about-cloud/JavaCore/blob/master/resource/markdown/collection/JavaCollections.md)
 * [集合框架 （第 02 篇） 源码分析：Map<K,V > 框架总览](https://github.com/about-cloud/JavaCore/blob/master/resource/markdown/collection/JavaMaps.md)
 * [集合框架 （第 03 篇） 源码分析：ArrayList<E>](https://github.com/about-cloud/JavaCore/blob/master/resource/markdown/collection/ArrayList.md)
@@ -190,6 +199,5 @@
 
 ### 联系作者:flags:：
 
-> :postbox:aboutcloud@163.com
->
-> :dizzy:[https://www.FooVv.com](https://www.foovv.com)
+> :postbox:linkedme@qq.com
+>
diff --git a/resource/markdown/algorithm/BasicSorting.md b/resource/markdown/algorithm/BasicSorting.md
@@ -0,0 +1,245 @@
+### 常见基础排序算法
+
+
+
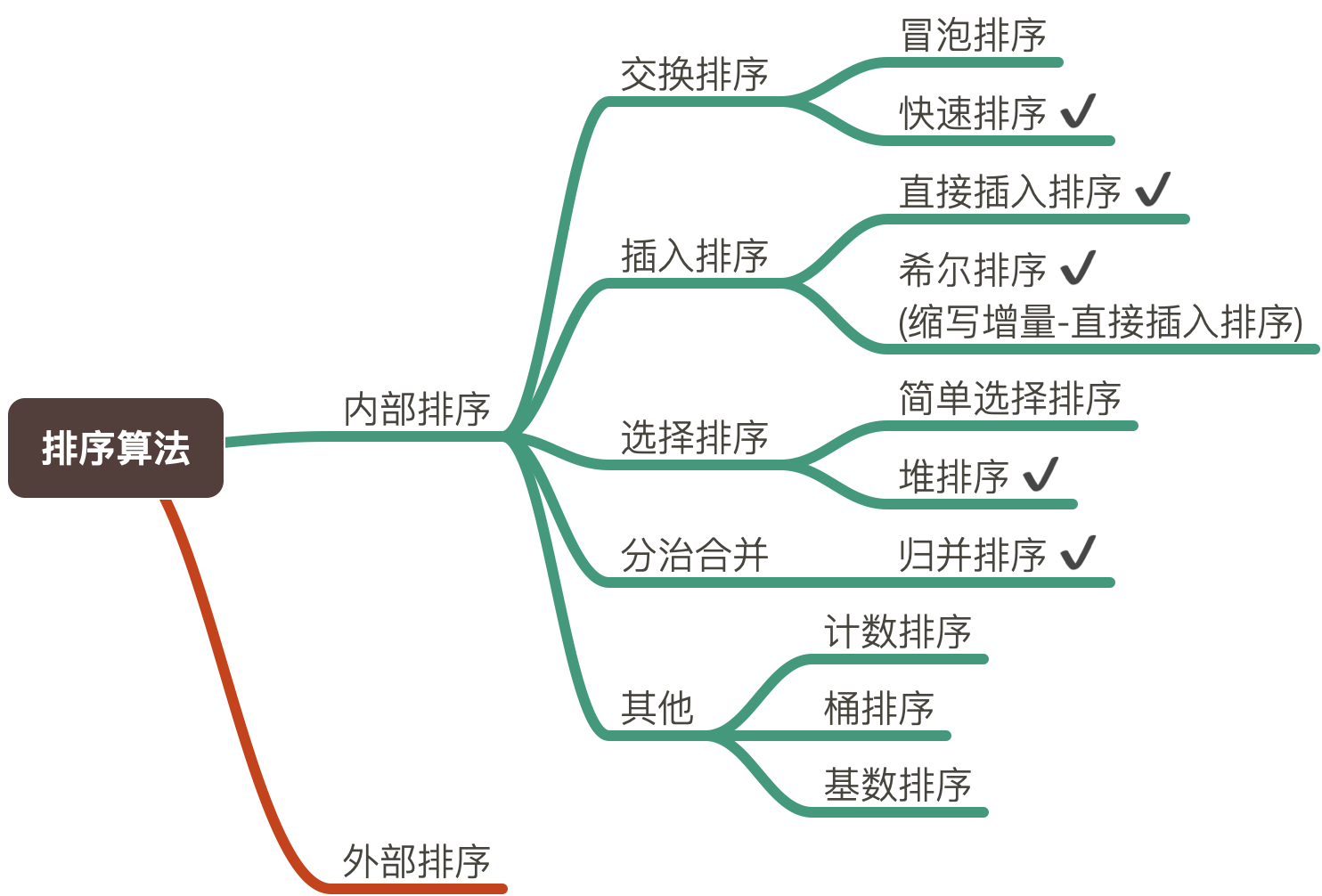+#### 排序算法分类
+
+![排序算法分类](https://i.loli.net/2019/06/10/5cfe3bf15a32392750.png)
+
+
+#### 时间复杂度
+
+| 排序算法     | 最好(时间复杂度)          | 平均(时间复杂度)          | 最坏(时间复杂度)          | 稳定性 | 空间复杂度                       |
+| ------------ | ------------------------- | ------------------------- | ------------------------- | ------ | -------------------------------- |
+| 冒泡排序     | **O**(n)                  | **O**(n<sup>2</sup>)      | **O**(n<sup>2</sup>)      | 稳定   | **O**(1)                         |
+| **快速排序** | **O**(n*log<sub>2</sub>n) | **O**(n*log<sub>2</sub>n) | **O**(n<sup>2</sup>)      | 不稳定 | **O**(log<sub>2</sub>n)~**O**(n) |
+| 直接插入排序 | **O**(n)                  | **O**(n<sup>2</sup>)      | **O**(n<sup>2</sup>)      | 稳定   | **O**(1)                         |
+| **希尔排序** | **O**(n)                  | **O**(n<sup>1.3</sup>)    | **O**(n<sup>2</sup>)      | 不稳定 | **O**(1)                         |
+| 简单选择排序 | **O**(n)                  | **O**(n<sup>2</sup>)      | **O**(n<sup>2</sup>)      | 不稳定 | **O**(1)                         |
+| **堆排序**   | **O**(n*log<sub>2</sub>n) | **O**(n*log<sub>2</sub>n) | **O**(n*log<sub>2</sub>n) | 不稳定 | **O**(1)                         |
+| **归并排序** | **O**(n*log<sub>2</sub>n) | **O**(n*log<sub>2</sub>n) | **O**(n*log<sub>2</sub>n) | 稳定   | **O**(n)                         |
+| 基数排序     | **O**(d*(r+n))            | **O**(d*(r+n))            | **O**(d*(r+n))            | 稳定   | **O**(r*d+n)                     |
+
+
+
+#### 各种复杂度效率比较图
+
+```java
+O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n^3) < O(n^n)
+```
+
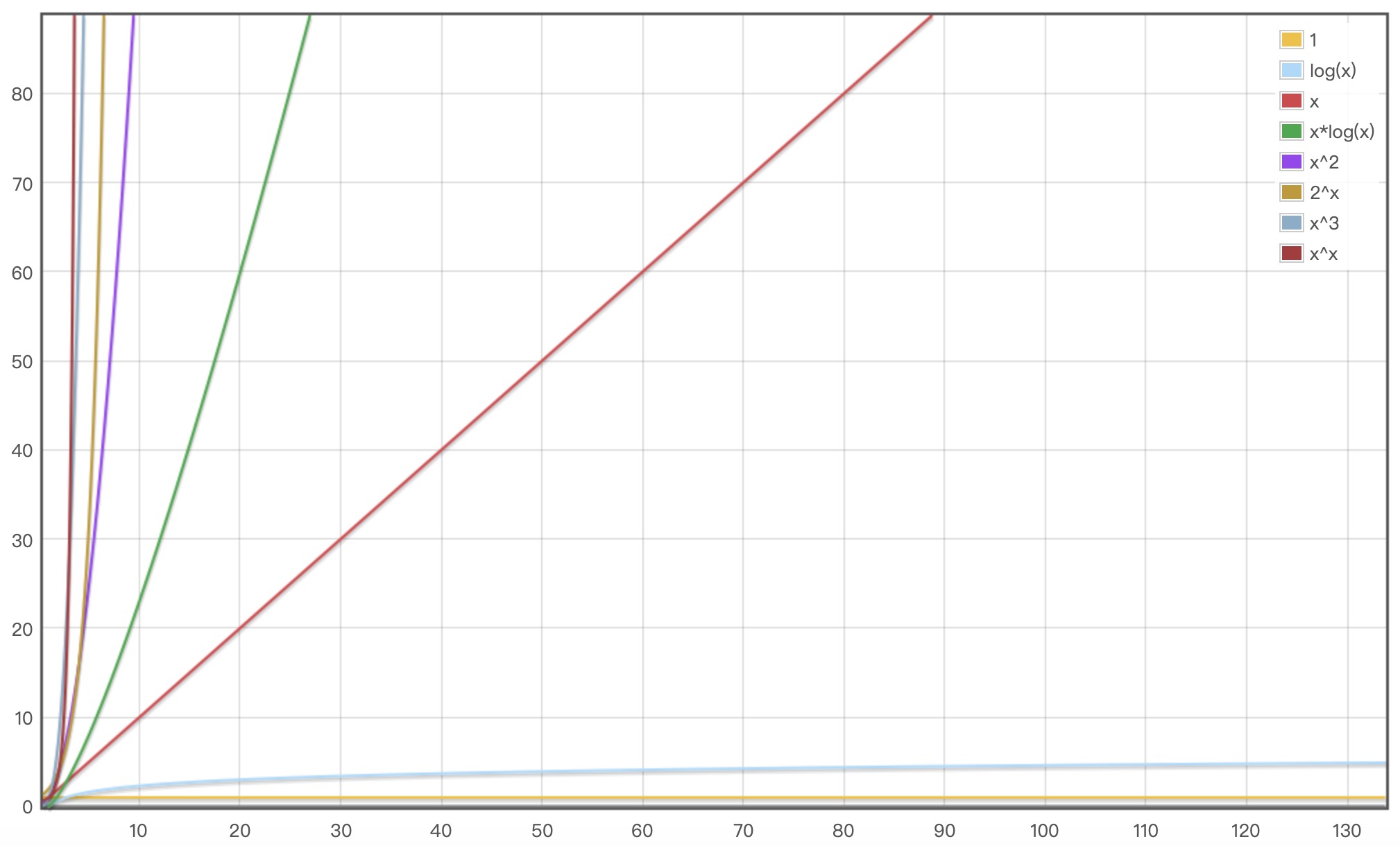+![各种时间复杂度效率比较图](https://i.loli.net/2019/06/11/5cff235ba9b9a93703.jpg)
+
+**说明：** n 越大，越能体现算法效率。当 n 比较小时，复杂度会有一波小交叉，上图不考虑 n 比较小的情况。
+
+
+
+##### 1. 冒泡排序 ★☆☆☆☆
+
+```java
+public void bubbleSort(int[] array) {
+    int temp;
+    // 外层移动基准元素索引
+    for (int i = 0; i < array.length - 1; i++) {
+        // 内层对基准元素与之后的每个做比较，冒泡排序
+        for (int j = i + 1; j < array.length; j++) {
+            // 大的值，向上冒泡
+            if ((temp = array[i]) > array[j]) {
+                array[i] = array[j];
+                array[j] = temp;
+            }
+        }
+    }
+}
+```
+
+
+
+##### 2. 快速排序 ★★★★★
+
+```java
+public void quickSort(int[] array, int left, int right) {
+    if (left < right) {
+        int i = left;
+        int j = right;
+        int temp = array[i];
+        
+        while (i < j) {
+            while (i < j && array[j] >= temp) {
+                j--;
+            }
+            if (i < j) {
+                array[i++] = array[j];
+            }
+            
+            while (i < j && array[i] <= temp) {
+                i++;
+            }
+            if (i < j) {
+                array[j--] = array[i];
+            }
+            
+            array[i] = temp;
+            quickSort(array, left, i - 1);
+            quickSort(array, i + 1, right);
+        }
+    }
+}
+```
+
+
+
+##### 3. 直接插入排序 ★★★☆☆
+
+```java
+public void insertionSort(int[] array) {
+    for (int i = 0; i < array.length; i++) {
+        int temp = array[i];
+        int j;
+        for (j = i; j > 0 && array[j - 1] > temp; j--) {
+            array[j] = array[j - 1];
+        }
+        if (array[j] > temp) {
+            array[j] = temp;
+        }
+    }
+}
+```
+
+
+
+##### 4. 希尔排序 ★★★☆☆
+
+```java
+public void shellSort(int[] array) {
+    // 增量
+    for (int d = array.length / 2; d > 0; d /= 2) {
+        // 分组
+        for (int x = 0; x < d; x++) {
+            // 直接插入排序(第 x 组的第2个元素起步)
+            for (int i = x + d; i < array.length; i += d) {
+                int temp = array[i];
+                int j = i;
+                for (; j > d && array[j - d] > temp; j -= d) {
+                    array[j] = array[j - d];
+                }
+                if (array[j] > temp) {
+                    array[j] = temp;
+                }
+            }
+        }
+    }
+}
+```
+
+
+
+##### 5. 简单选择排序 ★★☆☆☆
+
+```java
+public void selectionSort(int[] array) {
+    int minIndex;
+    int temp;
+    for (int i = 0; i < array.length - 1; i++) {
+        minIndex = i;
+        for (int j = i + 1; j < array.length; j ++) {
+            if (array[minIndex] > array[j]) {
+                minIndex = j;
+            }
+        }
+        if (minIndex > i) {
+            temp = array[i];
+            array[i] = array[minIndex];
+            array[minIndex] = temp;
+        }
+    }
+}
+```
+
+
+
+##### 6. 堆排序 ★★★★☆
+
+```java
+public void heapSort(int[] array) {
+	for (int i = array.length / 2 - 1; i >= 0; i--) {
+		adjustHeap(array, i, array.length);
+	}
+
+	for (int i = array.length - 1; i > 0; i--) {
+		swap(array, 0, i);
+		adjustHeap(array, 0, i);
+	}
+}
+
+private void adjustHeap(int[] array, int i, int length) {
+	int temp = array[i];
+
+	for (int j = i * 2 + 1; j < length; j = j * 2 + 1) {
+		if (j + 1 < length && array[j + 1] > array[j]) {
+			j++;
+		}
+		if (array[j] > temp) {
+			array[i] = array[j];
+			i = j;
+		} else {
+			break;
+		}
+	}
+	array[i] = temp;
+}
+
+private void swap(int[] array, int a, int b) {
+	int temp = array[a];
+	array[a] = array[b];
+	array[b] = temp;
+}
+```
+
+
+
+##### 7. 归并排序 ★★★★☆
+
+```java
+public void mergeSort(int[] array) {
+    int[] aux = new int[array.length];
+    sort(array, 0, array.length - 1, aux);
+}
+
+private void sort(int[] array, int left, int right,int[] aux) {
+	if (left < right) {
+        int mid = (left + right) / 2;
+        sort(array, left , mid, aux);
+        sort(array, mid + 1, right, aux);
+        merge(array, left, mid, right, aux);
+    }
+}
+
+private void merge(int[] array, int left, int mid, int right, int[] aux){
+    int l = left;
+    int m = mid + 1;
+    int t = 0;
+    
+    while (l <= mid && m <= right) {
+        if (array[l] <= array[m]) {
+            aux[t++] = array[l++];
+        } else {
+            aux[t++] = array[m++];
+        }
+    }
+    
+    // 填充剩余元素
+    while (l <= mid) {
+        aux[t++] = array[l++];
+    }
+    while (m <= right) {
+        aux[t++] = array[m++];
+    }
+    
+    t = 0;
+    while (left <= right) {
+        array[left++] = aux[t++];
+    }
+}
+```
+
diff --git a/resource/markdown/algorithm/BinaryTreeTraversal.md b/resource/markdown/algorithm/BinaryTreeTraversal.md
@@ -0,0 +1,120 @@
+### 二叉树的遍历 ★★★★★
+
+
+
+##### 0. TreeNode 结点
+
+```java
+private static class TreeNode<T> {
+    T data;
+    TreeNode left, right;
+
+    TreeNode(T data) {
+      this.data = data;
+    }
+    TreeNode() {
+    }
+}
+```
+
+
+
+##### 1. 递归调用 (深度优先遍历) ★☆☆☆☆
+
+```java
+public void preorderTraversal(TreeNode node) {
+    if (node == null) {
+      return;
+    }
+  // 可调整前、中、后序遍历
+  System.out.print(node.data);
+  preorderTraversal(node.left);
+  preorderTraversal(node.right);
+}
+```
+
+
+
+##### 2. 非递归遍历 - 基于栈 (深度优先遍历) ★★★☆☆
+
+```java
+public void preorderTraversalWithStack(TreeNode root) {
+    Stack<TreeNode> stack = new Stack<>();
+    TreeNode node = root;
+    while (node != null || !stack.isEmpty()) {
+      // 访问结点的数据，并且移动到左子结点
+      while (node != null) {
+        System.out.println(node.data);
+        stack.push(node);
+        node = node.left;
+      }
+      // 回溯，遍历右子结点
+      if (!stack.isEmpty()) {
+        node = stack.pop();
+        node = node.right;
+      }
+    }
+}
+```
+
+
+
+##### 3. 非递归遍历 - 基于队列 (层次遍历、广度优先遍历、O(n)) ★★★★☆
+
+```java
+public void levelorderTraversal(TreeNode root) {
+    if (root == null) {
+        return;
+    }
+    Queue<TreeNode> queue = new LinkedList<>();
+    queue.offer(root);
+    TreeNode node;
+    // 遍历队列
+    while (!queue.isEmpty()) {
+        // 从队列头部取出一个结点
+        node = queue.poll();
+        System.out.println(node.data);
+        // 将左右子结点放入队列尾部
+        if (node.left != null) {
+            queue.offer(node.left);
+        }
+    	if (node.right != null) {
+            queue.offer(node.right);
+    	}
+    }
+}
+```
+
+
+
+##### 4. Morris Traversal(莫里斯遍历、O(n)) ★★★★☆
+
+```java
+public void morrisTraversal(TreeNode root) {
+    TreeNode curr = root;
+    TreeNode prev;
+    while (curr != null) {
+        // 向左子结点遍历
+        if (curr.left != null) {
+            prev = curr.left;
+            while (prev.right != null && prev.right != curr) {
+                prev = prev.right;
+            }
+            // 右子结点的回溯指针绑定
+            if (prev.right == null) {
+                prev.right = curr;
+                curr = curr.left;
+            } else {
+                System.out.println(curr.data);
+                prev.right = null;
+                curr = curr.right;
+            }
+            // 向右子结点遍历
+        } else {
+            System.out.print(curr.data);
+            curr = curr.right;
+        }
+    }
+}
+```
+
