|
| 1 | +# 【数组中超过一半的数字】三种解法,最后一个解法太牛逼了! |
| 2 | + |
| 3 | +今天分享的题目来源于 LeetCode 上第 169 号问题:求众数(求数组中超过一半的数字)。题目难度为 Easy,目前通过率为 45.8% 。 |
| 4 | + |
| 5 | +最后一种解法 **Cool** !!! |
| 6 | + |
| 7 | +# 题目描述 |
| 8 | + |
| 9 | +给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。 |
| 10 | + |
| 11 | +你可以假设数组是非空的,并且给定的数组总是存在众数。 |
| 12 | + |
| 13 | +**示例 1:** |
| 14 | + |
| 15 | +``` |
| 16 | +输入: [3,2,3] |
| 17 | +输出: 3 |
| 18 | +``` |
| 19 | + |
| 20 | +**示例 2:** |
| 21 | + |
| 22 | +``` |
| 23 | +输入: [2,2,1,1,1,2,2] |
| 24 | +输出: 2 |
| 25 | +``` |
| 26 | + |
| 27 | +# 题目解析 |
| 28 | + |
| 29 | +题目意思很好理解:给你一个数组,里面有一个数字出现的次数超过了一半,你要找到这个数字并返回。 |
| 30 | + |
| 31 | +## 解法一:暴力解法 |
| 32 | + |
| 33 | +遍历整个数组,同时统计每个数字出现的次数。 |
| 34 | + |
| 35 | +最后将出现次数大于一半的元素返回即可。 |
| 36 | + |
| 37 | +### 动画描述 |
| 38 | + |
| 39 | +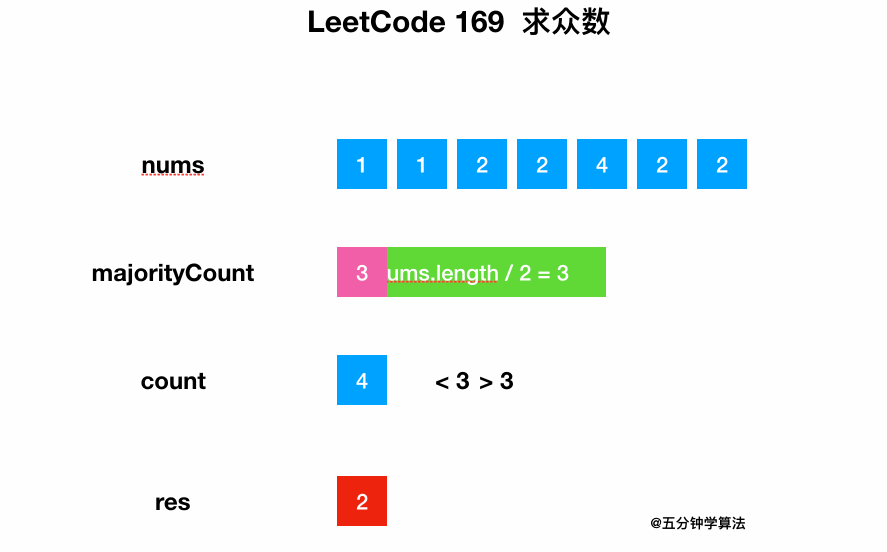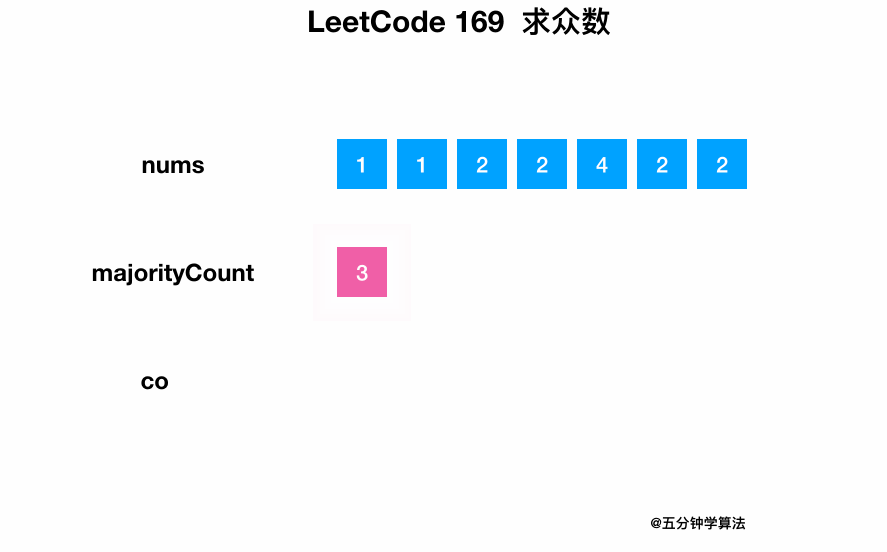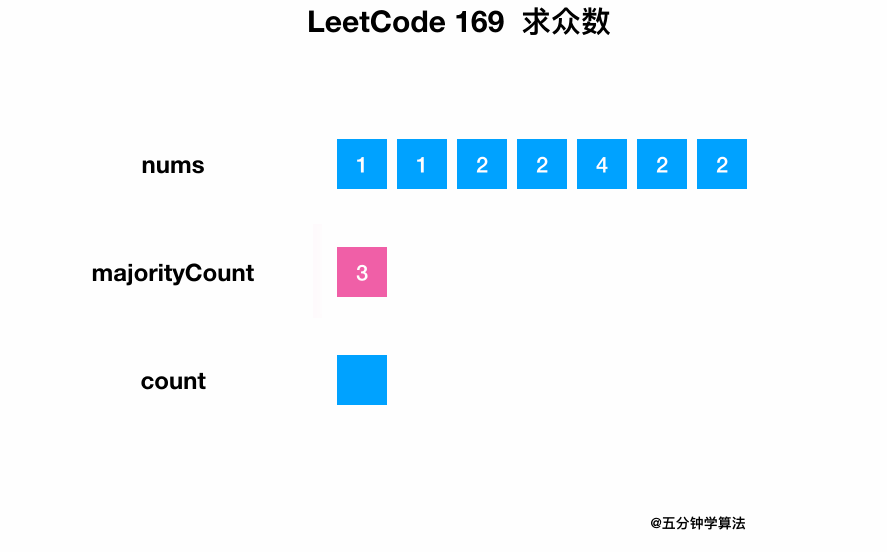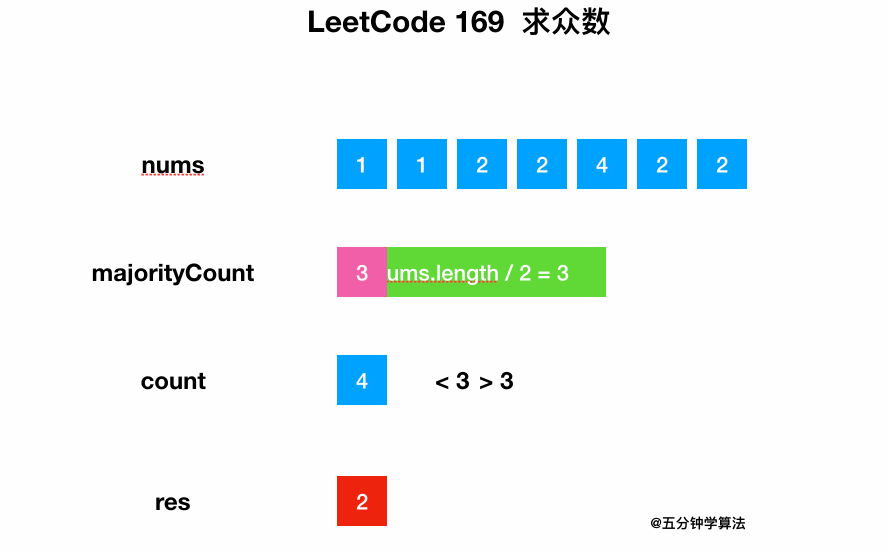 |
| 40 | + |
| 41 | +### **代码实现** |
| 42 | + |
| 43 | +```java |
| 44 | +class Solution { |
| 45 | + public int majorityElement(int[] nums) { |
| 46 | + int majorityCount = nums.length/2; |
| 47 | + |
| 48 | + for (int num : nums) { |
| 49 | + int count = 0; |
| 50 | + for (int elem : nums) { |
| 51 | + if (elem == num) { |
| 52 | + count += 1; |
| 53 | + } |
| 54 | + } |
| 55 | + if (count > majorityCount) { |
| 56 | + return num; |
| 57 | + } |
| 58 | + |
| 59 | + } |
| 60 | + } |
| 61 | +} |
| 62 | +``` |
| 63 | + |
| 64 | +### 复杂度分析 |
| 65 | + |
| 66 | +**时间复杂度**:O(n<sup>2</sup>) |
| 67 | + |
| 68 | +暴力解法包含两重嵌套的 for 循环,每一层 n 次迭代,因此时间复杂度为 O(n<sup>2</sup>) 。 |
| 69 | + |
| 70 | +**空间复杂度**:O(1) |
| 71 | + |
| 72 | +暴力解法没有分配任何与输入规模成比例的额外的空间,因此空间复杂度为 O(1)。 |
| 73 | + |
| 74 | +## 解法二:哈希表法 |
| 75 | + |
| 76 | +这个问题可以视为查找问题,对于查找问题往往可以使用时间复杂度为 O(1) 的 **哈希表**,通过以空间换时间的方式进行优化。 |
| 77 | + |
| 78 | +直接遍历整个 **数组** ,将每一个数字(num)与它出现的次数(count)存放在 **哈希表** 中,同时判断该数字出现次数是否是最大的,动态更新 maxCount,最后输出 maxNum。 |
| 79 | + |
| 80 | +### 动画描述 |
| 81 | + |
| 82 | + |
| 83 | + |
| 84 | +### 代码实现 |
| 85 | + |
| 86 | +```java |
| 87 | +class Solution { |
| 88 | + public int majorityElement(int[] nums) { |
| 89 | + Map<Integer, Integer> map = new HashMap<>(); |
| 90 | + // maxNum 表示元素,maxCount 表示元素出现的次数 |
| 91 | + int maxNum = 0, maxCount = 0; |
| 92 | + for (int num: nums) { |
| 93 | + int count = map.getOrDefault(num, 0) + 1; |
| 94 | + map.put(num, count); |
| 95 | + if (count > maxCount) { |
| 96 | + maxCount = count; |
| 97 | + maxNum = num; |
| 98 | + } |
| 99 | + } |
| 100 | + return maxNum; |
| 101 | + } |
| 102 | +} |
| 103 | +``` |
| 104 | + |
| 105 | +### 复杂度分析 |
| 106 | + |
| 107 | +**时间复杂度**:O(n) |
| 108 | + |
| 109 | +总共有一个循环,里面哈希表的插入是常数时间的,因此时间复杂度为 O(n)。 |
| 110 | + |
| 111 | +**空间复杂度**:O(n) |
| 112 | + |
| 113 | +哈希表占用了额外的空间 O(n),因此空间复杂度为 O(n)。 |
| 114 | + |
| 115 | +## 解法三:摩尔投票法 |
| 116 | + |
| 117 | +再来回顾一下题目:寻找数组中超过一半的数字,这意味着数组中**其他数字出现次数的总和都是比不上这个数字出现的次数** 。 |
| 118 | + |
| 119 | +即如果把 该众数记为 `+1` ,把其他数记为 `−1` ,将它们全部加起来,和是大于 0 的。 |
| 120 | + |
| 121 | +所以可以这样操作: |
| 122 | + |
| 123 | +* 设置两个变量 candidate 和 count,**candidate** 用来保存数组中遍历到的某个数字,**count** 表示当前数字的出现次数,一开始 **candidate** 保存为数组中的第一个数字,**count** 为 1 |
| 124 | +* 遍历整个数组 |
| 125 | +* 如果数字与之前 **candidate** 保存的数字相同,则 **count** 加 1 |
| 126 | +* 如果数字与之前 **candidate** 保存的数字不同,则 **count** 减 1 |
| 127 | +* 如果出现次数 **count** 变为 0 ,**candidate** 进行变化,保存为当前遍历的那个数字,并且同时把 **count** 重置为 1 |
| 128 | +* 遍历完数组中的所有数字即可得到结果 |
| 129 | + |
| 130 | +### 动画描述 |
| 131 | + |
| 132 | + |
| 133 | + |
| 134 | +### 代码实现 |
| 135 | + |
| 136 | +```java |
| 137 | +class Solution { |
| 138 | + public int majorityElement(int[] nums) { |
| 139 | + int candidate = nums[0], count = 1; |
| 140 | + for (int i = 1; i < nums.length; ++i) { |
| 141 | + if (count == 0) { |
| 142 | + candidate = nums[i]; |
| 143 | + count = 1; |
| 144 | + } else if (nums[i] == candidate) { |
| 145 | + count++; |
| 146 | + } else{ |
| 147 | + count--; |
| 148 | + } |
| 149 | + } |
| 150 | + return candidate; |
| 151 | + } |
| 152 | +} |
| 153 | +``` |
| 154 | + |
| 155 | +### 复杂度分析 |
| 156 | + |
| 157 | +**时间复杂度**:O(n) |
| 158 | + |
| 159 | +总共只有一个循环,因此时间复杂度为 O(n)。 |
| 160 | + |
| 161 | +**空间复杂度**:O(1) |
| 162 | + |
| 163 | +只需要常数级别的额外空间,因此空间复杂度为 O(1)。 |
0 commit comments