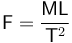Newton (unit)

Not to be confused with Newton scale, a rarely used non-SI temperature scale.

Newton
Unit system	SI derived unit
Unit of	Force
Symbol	N
Named after	Sir Isaac Newton
In SI base units:	kg⋅m⋅s-2

The newton (symbol: N) is the International System of Units (SI) derived unit of force. It is named after Isaac Newton in recognition of his work on classical mechanics, specifically Newton's second law of motion.

See below for the conversion factors and SI unitizing.

Definition

One newton is the force needed to accelerate one kilogram of mass at the rate of one metre per second squared.

In 1946 Conférence Générale des Poids et Mesures (CGPM) resolution 2 standardized the unit of force in the MKS system of units to be the amount needed to accelerate 1 kilogram of mass at the rate of 1 metre per second squared. In 1948 the 9th CGPM resolution 7 adopted the name "newton" for this force. The MKS system then became the blueprint for today's SI system of units. The newton thus became the standard unit of force in le Système International d'Unités (SI), or International System of Units.

This SI unit is named after Isaac Newton. As with every International System of Units (SI) unit named for a person, the first letter of its symbol is upper case (N). However, when an SI unit is spelled out in English, it should always begin with a lower case letter (newton)—except in a situation where any word in that position would be capitalized, such as at the beginning of a sentence or in material using title case. Note that "degree Celsius" conforms to this rule because the "d" is lowercase.— Based on The International System of Units, section 5.2.

Newton's second law of motion states that F = ma, where F is the force applied, m is the mass of the object receiving the force, and a is the acceleration of the object. The newton is therefore:

F	=	m	⋅	a
1 N	=	1 kg	⋅	m/s2

where the following symbols are used for the units:

N: newton

kg: kilogram

m: metre

s: second.

In dimensional analysis:

${\mathsf F} = \frac{\mathsf {ML}} {{\mathsf T}^2}$

where

F: force

M: mass

L: length

T: time.

Examples

At average gravity on earth, (conventionally g = 9.80665 m/s²), a kilogram mass exerts a force of about 9.8 newtons, and one newton is the force exerted by about half a medium-sized apple.

1 N = 0.102 kg × 9.80665 m/s²    (0.102 kg ≅ 100 g)

The weight of an average adult exerts a force of about 550 - 800 N.

566 N = 57.7 kg (average adult weight in Asia) × 9.80665 m/s²

791 N = 80.7 kg (average adult weight in North America) × 9.80665 m/s²

Bench pressing 100 pounds (45 kg) takes a little under 450 N of force.

441 N = 45 kg × 9.80665 m/s²

Commonly seen as kilonewtons

A newton is not much force, so it is common to see forces expressed in kilonewtons, or kN, where 1 kN = 1000 N. For example, the tractive effort of a Class Y steam train and the thrust of a an F100 fighter jet are both around 130 kN.

Where units are commonly in kilonewtons, a common rule of thumb is to multiply the kilonewton value by a factor of 100 to get the kilograms. One kilonewton, 1 kN, is 102.0 kgf, or about 100 kg of load.

1 kN = 102 kg × 9.81 m/s²    (102 kg ≅ 100 kg)

So for example, a platform rated at 321 kilonewtons (72,000 lb_f) will safely support a 32,100 kilograms (70,800 lb) load.

Specifications in kilonewtons are common in safety specifications for:

• the holding values of fasteners, Earth anchors, and more, in the building industry.
• working loads in tension and in shear.
• rock climbing equipment.
• clamping forces of the various moulds in injection moulding machines used to manufacture plastic parts.

Conversion factors

Units of force

	newton (SI unit)	dyne	kilogram-force, kilopond	pound-force	poundal
1 N	≡ 1 kg⋅m/s2	= 105 dyn	≈ 0.10197 kp	≈ 0.22481 lbF	≈ 7.2330 pdl
1 dyn	= 10−5 N	≡ 1 g⋅cm/s2	≈ 1.0197 × 10−6 kp	≈ 2.2481 × 10−6 lbF	≈ 7.2330 × 10−5 pdl
1 kp	= 9.80665 N	= 980665 dyn	≡ gn⋅(1 kg)	≈ 2.2046 lbF	≈ 70.932 pdl
1 lbF	≈ 4.448222 N	≈ 444822 dyn	≈ 0.45359 kp	≡ gn⋅(1 lb)	≈ 32.174 pdl
1 pdl	≈ 0.138255 N	≈ 13825 dyn	≈ 0.014098 kp	≈ 0.031081 lbF	≡ 1 lb⋅ft/s2
The value of gn as used in the official definition of the kilogram-force is used here for all gravitational units.

Three approaches to mass and force units

Base	force, length, time		weight, length, time		mass, length, time
Force (F)	F = m⋅a = w⋅a/g		F = m⋅a/gc = w⋅a/g		F = m⋅a = w⋅a/g
Weight (w)	w = m⋅g		w = m⋅g/gc ≈ m		w = m⋅g
System	BG	GM	EE	M	AE	CGS	MTS	SI
Acceleration (a)	ft/s2	m/s2	ft/s2	m/s2	ft/s2	Gal	m/s2	m/s2
Mass (m)	slug	hyl	lbm	kg	lb	g	t	kg
Force (F)	lb	kp	lbF	kp	pdl	dyn	sn	N
Pressure (p)	lb/in2	at	PSI	atm	pdl/ft2	Ba	pz	Pa

Standard prefixes for the SI units of measure

Multiples	Prefix name		deca	hecto	kilo	mega	giga	tera	peta	exa	zetta	yotta
	Prefix symbol		da	h	k	M	G	T	P	E	Z	Y
	Factor	100	101	102	103	106	109	1012	1015	1018	1021	1024
Fractions	Prefix name		deci	centi	milli	micro	nano	pico	femto	atto	zepto	yocto
	Prefix symbol		d	c	m	μ	n	p	f	a	z	y
	Factor	100	10−1	10−2	10−3	10−6	10−9	10−12	10−15	10−18	10−21	10−24

See also

• Force gauge
• International System of Units (SI)
• Joule, SI unit of energy, 1 newton exerted over a distance of 1 metre
• Kilogram-force, force exerted by Earth's gravity at sea level on one kilogram of mass
• Kip (unit)
• Pascal, SI unit of pressure, 1 newton acting on an area of 1 square metre
• Orders of magnitude (force)
• Pound (force)
• Sthène
• Newton metre, SI unit of torque