List of probabilistic proofs of non-probabilistic theorems

Probability theory routinely uses results from other fields of mathematics (mostly, analysis). The opposite cases, collected below, are relatively rare; however, probability theory is used systematically in combinatorics via the probabilistic method. They are particularly used for non-constructive proofs.

Analysis

• Normal numbers exist. Moreover, computable normal numbers exist. These non-probabilistic existence theorems follow from probabilistic results: (a) a number chosen at random (uniformly on (0,1)) is normal almost surely (which follows easily from the strong law of large numbers); (b) some probabilistic inequalities behind the strong law. The existence of a normal number follows from (a) immediately. The proof of the existence of computable normal numbers, based on (b), involves additional arguments. All known proofs use probabilistic arguments.
• Dvoretzky's theorem which states that high-dimensional convex bodies have ball-like slices is proved probabilistically. No deterministic construction is known, even for many specific bodies.
• The diameter of the Banach–Mazur compactum was calculated using a probabilistic construction. No deterministic construction is known.
• The original proof that the Hausdorff–Young inequality cannot be extended to 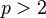$p > 2$ is probabilistic. The proof of the de Leeuw–Kahane–Katznelson theorem (which is a stronger claim) is partially probabilistic.
• The first construction of a Salem set was probabilistic. Only in 1981 did Kaufman give a deterministic construction.
• Every continuous function on an compact interval can be uniformly approximated by polynomials, which is the Weierstrass approximation theorem. A probabilistic proof uses the weak law of large numbers. Non-probabilistic proofs were available earlier.
• Existence of a nowhere differentiable continuous function follows easily from properties of Wiener process. A non-probabilistic proof was available earlier.
• Stirling's formula was first discovered by Abraham de Moivre in his `The Doctrine of Chances' (with a constant identified later by Stirling) in order to be used in probability theory. Several probabilistic proofs of Stirling's formula (and related results) were found in the 20th century.

• The only bounded harmonic functions defined on the whole plane are constant functions by Liouville's theorem. A probabilistic proof via two-dimensional Brownian motion is well known. Non-probabilistic proofs were available earlier.
• Non-tangential boundary values of an analytic or harmonic function exist at almost all boundary points of non-tangential boundedness. This result (Privalov's theorem), and several results of this kind, are deduced from martingale convergence. Non-probabilistic proofs were available earlier.
• The boundary Harnack principle is proved using Brownian motion (see also). Non-probabilistic proofs were available earlier.
• Euler's Basel sum, $\qquad \sum_{n=1}^\infin \frac{1}{n^2} = \frac{\pi^2}{6},$ can be demonstrated by considering the expected exit time of planar Brownian motion from an infinite strip. A number of other less well-known identities can be deduced in a similar manner.

• The Picard Theorem can be proved using the winding properties of planar Brownian motion.

Combinatorics

• A number of theorems stating existence of graphs (and other discrete structures) with desired properties are proved by the probabilistic method. Non-probabilistic proofs are available for some of them.
• The maximum-minimums identity admits a probabilistic proof.

Algebra

• The fundamental theorem of algebra can be proved using two-dimensional Brownian motion. Non-probabilistic proofs were available earlier.
• The index theorem for elliptic complexes is proved using probabilistic methods (rather than heat equation methods). A non-probabilistic proof was available earlier.

Topology and geometry

• A smooth boundary is evidently two-sided, but a non-smooth (especially, fractal) boundary can be quite complicated. It was conjectured to be two-sided in the sense that the natural projection of the Martin boundary to the topological boundary is at most 2 to 1 almost everywhere. This conjecture is proved using Brownian motion, local time, stochastic integration, coupling, hypercontractivity etc. (see also). Known non-probabilistic approaches give weaker results: at most 10 sides in four (and more) dimensions; at most 4 sides in three dimensions; and 2 sides on the plane.
• The Loewner's torus inequality relates the area of a compact surface (topologically, a torus) to its systole. It can be proved most easily by using the probabilistic notion of variance. A non-probabilistic proof was available earlier.
• The weak halfspace theorem for minimal surfaces states that any complete minimal surface of bounded curvature which is not a plane is not contained in any halfspace. This theorem is proved using a coupling between Brownian motions on minimal surfaces. A non-probabilistic proof was available earlier.

Number theory

• The normal number theorem (1909), due to Émile Borel, could be one of the first examples of the probabilistic method, providing the first proof of existence of normal numbers, with the help of the first version of the strong law of large numbers (see also the first item of the section Analysis).
• The Rogers–Ramanujan identities are proved using Markov chains. A non-probabilistic proof was available earlier.

Quantum theory

• Non-commutative dynamics (called also quantum dynamics) is formulated in terms of Von Neumann algebras and continuous tensor products of Hilbert spaces. Several results (for example, a continuum of mutually non-isomorphic models) are obtained by probabilistic means (random compact sets and Brownian motion). One part of this theory (so-called type III systems) is translated into the analytic language and is developing analytically; the other part (so-called type II systems) exists still in the probabilistic language only.
• Tripartite quantum states can lead to arbitrary large violations of Bell inequalities (in sharp contrast to the bipartite case). The proof uses random unitary matrices. No other proof is available.

Information theory

• The proof of Shannon's channel coding theorem uses random coding to show the existence of a code that achieves channel capacity.

See also

• Probabilistic method

External links

• Probabilistic Proofs of Analytic Facts at MathOverflow

• Karel de Leeuw, Yitzhak Katznelson and Jean-Pierre Kahane, Sur les coefficients de Fourier des fonctions continues. (French) C. R. Acad. Sci. Paris Sér. A–B 285:16 (1977), A1001–A1003.
• .
• .
• (see Exercise (2.17) in Section V.2, page 187).
• See Fatou's theorem.
• .
• .
• .
• .
• .
• .
• .
• As long as we have no article on Martin boundary, see Compactification (mathematics)#Other compactification theories.
• (see Section 6).
• . author's site
• .
• . Also arXiv:0805.0556.
• . Also arXiv:math.CO/0001078.
• .
• . Also arXiv:math.FA/0210457.
• .
• . Also arXiv:math.OA/0405276.
• . Also arXiv:0705.3280.