Getransponeerde matrix

In de lineaire algebra is de getransponeerde matrix of kortweg de getransponeerde van een matrix $A$ de matrix die ontstaat door een van de onderstaande twee acties op $A$ uit te voeren:

• Schrijf de rijen van $A$ als de kolommen van $A^{\text{T}}$.
• Schrijf de kolommen van $A$ als de rijen van $A^{\text{T}}$.

Het bepalen van de getransponeerde matrix $A^{\text{T}}$ van een matrix $A$ en hetzelfde nog een keer uitvoeren, zodat $A$ er weer komt.

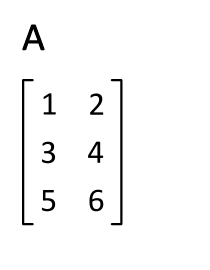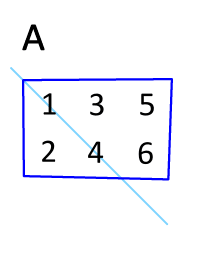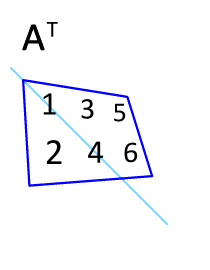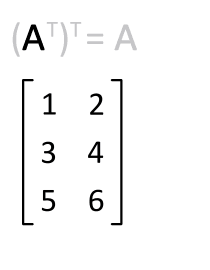
Als $A$ een vierkante matrix is komt dat er op neer dat $A$ om zijn hoofddiagonaal wordt gespiegeld. Als men hetzelfde voor de tweede keer uitvoert, is het resultaat de oorspronkelijke matrix $A$, ook als $A$ geen vierkante matrix is.

$A^{\text{T}}$ wordt ook geschreven als $A^{\top }$ of als $A'$. De notatie $A'$ wordt in MATLAB voor de getransponeerde matrix van $A$ gebruikt.

De Britse wiskunde Arthur Cayley heeft de getransponeerde matrix in 1858 ingevoerd.

Definitie

De getransponeerde matrix van een $m\times n$-matrix $A$ is de $n\times m$-matrix $A^{\text{T}}$ gedefinieerd door:

$A_{ij}^{\text{T}}=A_{ji}$ voor $1\leq i\leq n,\quad 1\leq j\leq m$

Voorbeelden

• ${\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\text{T}}={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}$

• ${\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\text{T}}={\begin{bmatrix}1&3\\2&4\end{bmatrix}}$

Eigenschappen

Voor de matrices $A$ en $B$ en de scalair $c$ gelden de volgende eigenschappen van de transpositie-operatie:

• $(A^{\text{T}})^{\text{T}}=A$

De getransponeerde matrix van een getransponeerde matrix is de oorspronkelijke matrix. Transponeren is een involutie, een bewerking die haar eigen inverse is.

• $(A+B)^{\text{T}}=A^{\text{T}}+B^{\text{T}}$

Transponeren behoudt optelling.

• $(AB)^{\text{T}}=B^{\text{T}}A^{\text{T}}$

Merk op dat de volgorde van de factoren omdraait. Hieruit kan worden afgeleid dat een vierkante matrix $A$ inverteerbaar is dan en slechts dan als $A^{\text{T}}$ inverteerbaar is en in dat geval is $(A^{-1})^{\text{T}}=(A^{\text{T}})^{-1}.$ Dit resultaat kan worden uitgebreid naar het algemene geval van meer dan twee matrices. Dan geldt $(AB\ldots C)^{\text{T}}=C^{\text{T}}\ldots B^{\text{T}}A^{\text{T}}$.

• $(cA)^{\text{T}}=cA^{\text{T}}$

De getransponeerde van een scalair is dezelfde scalair. Samen met (2) volgt daaruit dat transponeren een lineaire afbeelding is van de vectorruimte van $m\times n$-matrices naar de ruimte van alle $n\times m$-matrices.

• ${\text{sp}}(A^{\text{T}})={\text{sp}}(A)$

Het spoor van een vierkante matrix is gelijk aan het spoor van zijn getransponeerde matrix.

• $\det(A^{\text{T}})=\det(A)$

De determinant van een vierkante matrix is gelijk aan de determinant van zijn getransponeerde matrix.

• ${\text{rang}}(A^{\mathrm {T} })={\text{rang}}(A)$

De rang van iedere matrix $A$ is gelijk aan de rang van de getransponeerde matrix $A^{T}$ van $A$

• Het inwendige product van twee kolomvectoren $a$ en $b$ kan worden berekend als

$a\cdot b=a^{\mathrm {T} }b$

• Als de matrix $A$ alleen reële elementen heeft, dan is $A^{\text{T}}A$ een positief-semidefiniete matrix.
• Als $A$ een matrix is over een lichaam/veld, dan is $A$ gelijksoortig met $A^{\text{T}}.$
• $(A^{\text{T}})^{-1}=(A^{-1})^{\text{T}}$

Voor een inverteerbare matrix $A$ is de getransponeerde van de inverse matrix de inverse van de getransponeerde.

• Als $A$ een vierkante matrix is, dan zijn de eigenwaardes gelijk aan de eigenwaardes van zijn getransponeerde matrix.

Matrices met bijzondere eigenschappen onder transpositie

• Een vierkante matrix die gelijk is aan zijn getransponeerde wordt een symmetrische matrix genoemd, dat wil zeggen dat $A$ symmetrisch is als geldt

$A^{\text{T}}=A$

• Een vierkante matrix waarvan de getransponeerde ook de inverse matrix is, is een orthogonale matrix. Dat wil zeggen dat de matrix $A$ orthogonaal is als geldt

$AA^{\text{T}}=A^{\text{T}}A=I$, waarin $I$ de eenheidsmatrix is

dus

$A^{\text{T}}=A^{-1}$

De kolommen van $A$ zijn orthonormaal.

• Een vierkante matrix die gelijk is aan de tegengestelde van zijn getransponeerde matrix, wordt een antisymmetrische matrix genoemd. Dat wil zeggen dat de matrix $A$ antisymmetrisch is als

$A^{\text{T}}=-A$

• Een hermitische matrix is een matrix die gelijk is aan de geconjugeerde getransponeerde matrix ervan, genoteerd

${\overline {A}}^{\text{T}}$

Dit wordt vaak afgekort tot $A^{*}$. Dus $A^{*}={\overline {A}}^{\text{T}}$

• Een normale matrix is een matrix die commuatief is met de geconjugeerde getransponeerde matrix ervan:

$A\ {\overline {A}}^{\text{T}}\ =\ {\overline {A}}^{\text{T}}\ A$

Voetnoten