Espaço conexo: diferenças entre revisões

← Ver a alteração anterior Ver a alteração posterior →

Conteúdo apagado Conteúdo adicionado

Em linha

Revisão das 23h53min de 3 de abril de 2023

De cima para baixo: os espaços vermelho A, magenta B, amarelo C e laranja D são todos **conexos**, enquanto o espaço verde E (composto pelos subconjuntos E1, E2, E3 e E4) é **desconexo**. Para além disso, A e B são também **simplesmente conexos** (género 0), enquanto C e D não o são: C tem género 1 e D tem género 4.

Em topologia, conexidade ^{(português brasileiro)} ou conectividade ^{(português europeu)} é a propriedade de um espaço conexo, isto é, um espaço topológico que não pode ser representado como a união de dois ou mais conjuntos abertos disjuntos e não-vazios.^[1]

Definição

Uma cisão de um conjunto é a decomposição $X=A\cup B$ em dois abertos disjuntos. Todo conjunto admite a cisão trivial em que $A=X$ e $B=\emptyset$ . Um conjunto chama-se conexo quando admite apenas a cisão trivial.^[1]

Equivalências

Os subconjuntos $\emptyset$ e $X$ são, ao mesmo tempo, abertos e fechados em qualquer topologia de $X$ . Assim, equivalentemente, se eles são os únicos conjuntos abertos e fechados, então $X$ é conexo. Por outro lado, se existe $A$ não-vazio aberto e fechado em $X$ , então $X$ é desconexo.^[2]

Exemplos

Um espaço conexo que não é conexo por arcos.

$\mathbb {R}$ e $\mathbb {C}$ são conexos, enquanto $\mathbb {N} ,$ $\mathbb {Z}$ e $\mathbb {Q}$ são desconexos.
Em $\mathbb {R}$ , os únicos subconjuntos conexos são os intervalos.^[3]
$R-\{0\}$ é desconexo pois possui a cisão não-trivial $(-\infty ,0)\cup (0,+\infty )$ .^[1]

Propriedades

A imagem de um conexo por uma aplicação contínua é um conexo.^[4]
Todo conjunto homeomorfo a um conexo é conexo.^[4]
A união de uma família de conjutnos conexos que possuam um ponto em comum é conexa.^[5]
O produto cartesiano de dois conjuntos é conexo se, e somente se, ambos são conexos.^[5]
O fecho de um conjunto conexo é conexo.^[6]

Conexo por caminhos

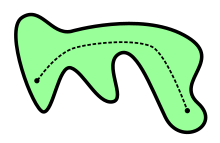
Um tipo de conexidade mais estrita é a conexidade por caminhos.^[7]

Um caminho num conjunto $X\subset \mathbb {R} ^{n}$ é uma função contínua definida num intervalo real que passa por pontos de $X$ . Dois pontos podem ser ligados por um caminho quando existe um caminho $f$ tal que esses pontos estejam na imagem de $f$ .^[8] Um conjunto se diz conexo por caminhos quando quaisquer dois pontos podem ser ligados por um caminho.^[8]

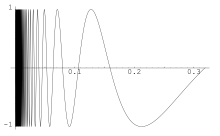
Todo conjunto conexo por caminhos é conexo, mas a recíproca é falsa.^[9] Por exemplo, no $\mathbb {R} ^{2},$ o gráfico da função $f(x)={\mbox{sen}}{\frac {1}{x}}$ para $0<x\leq 1$ com a origem $(0,0)$ é conexo mas não é conexo por caminhos.^[9]

Entretanto, no $\mathbb {R} ^{n}$ , um conjunto aberto é conexo se, e somente se, é conexo por caminhos.^[10]

Componentes conexas

Uma componente conexa de um espaço topológico é um subespaço conexo maximal.

Ver também

Referências

↑ ^a ^b ^c Lima 1981, p. 54.
↑ Lima 1981, p. 55.
↑ Lima 1981, p. 55, Teorema 31.
↑ ^a ^b Lima 1981, p. 55, Teorema 30.
↑ ^a ^b Lima 1981, p. 57, Teorema 33.
↑ Lima 1981, p. 59, Teorema 35.
↑ Lima 1981, p. 59.
↑ ^a ^b Lima 1981, pp. 59-60.
↑ ^a ^b Lima 1981, p. 61.
↑ Lima 1981, p. 61, Teorema 36.

Bibliografia

Lima, Elon Lages (1981). Curso de análise, Volume 2. Instituto de Matemática Pura e Aplicada. Rio de Janeiro: Instituto de Matemática Pura e Aplicada
Munkres, James R. (2000), Topology, ISBN 9780131816299, Prentice Hall, Incorporated .

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o.

[FOOTNOTELima198154-1] Lima 1981, p. 54.

[FOOTNOTELima198155-2] Lima 1981, p. 55.

[FOOTNOTELima198155Teorema_31-3] Lima 1981, p. 55, Teorema 31.

[FOOTNOTELima198155Teorema_30-4] Lima 1981, p. 55, Teorema 30.

[FOOTNOTELima198157Teorema_33-5] Lima 1981, p. 57, Teorema 33.

[FOOTNOTELima198159Teorema_35-6] Lima 1981, p. 59, Teorema 35.

[FOOTNOTELima198159-7] Lima 1981, p. 59.

[FOOTNOTELima198159-60-8] Lima 1981, pp. 59-60.

[FOOTNOTELima198161-9] Lima 1981, p. 61.

[FOOTNOTELima198161Teorema_36-10] Lima 1981, p. 61, Teorema 36.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

@@ Linha 1: / Linha 1: @@
 {{Mais notas|data=julho de 2013}}
 [[Imagem:Simply connected, connected, and non-connected spaces.svg|thumb|De cima para baixo: os espaços vermelho ''A'', magenta ''B'', amarelo ''C'' e laranja ''D'' são todos '''conexos''', enquanto o espaço verde ''E'' (composto pelos [[subconjunto]]s E1, E2, E3 e E4) é '''desconexo'''. Para além disso, ''A'' e ''B'' são também '''[[Grupo fundamental|simplesmente conexos]]''' ([[Género (matemática)|género]] 0), enquanto ''C'' e ''D'' não o são: ''C'' tem género 1 e ''D'' tem género 4.]]
 Em [[Topologia (matemática)|topologia]], {{PBPE|conexidade|conectividade}} é a propriedade de um '''espaço conexo''', isto é, um espaço topológico que não pode ser representado como a união de dois ou mais conjuntos abertos disjuntos e não-vazios.{{Sfn|Lima|1981|p=54}}
@@ Linha 27: / Linha 25: @@
 * O [[produto cartesiano]] de dois conjuntos é conexo se, e somente se, ambos são conexos.{{Sfn|Lima|1981|p=57|loc=Teorema 33}}
 * O [[fecho|fecho]] de um conjunto conexo é conexo.{{Sfn|Lima|1981|p=59|loc=Teorema 35}}
-== Componentes conexas ==
-* Uma '''componente conexa''' de um espaço topológico é um subespaço conexo maximal.
 == Conexo por caminhos ==
@@ Linha 41: / Linha 36: @@
 Entretanto, no <math>\R^n</math>, um [[conjunto aberto]] é conexo se, e somente se, é conexo por caminhos.{{Sfn|Lima|1981|p=61|loc=Teorema 36}}
+== Componentes conexas ==
+* Uma '''componente conexa''' de um espaço topológico é um subespaço conexo maximal.
 == Ver também ==
@@ Linha 47: / Linha 45: @@
 {{Referências}}
-* {{Citation | last1=Lima | first1=Elon L. | author1-link=Elon Lages Lima | title=Curso de Análise Vol.2 | publisher=[[IMPA]] | location=Rio De Janeiro | isbn=85-244-0049-8 | year=2006}}.
-* {{Citation | last1=Munkres | first1=James R. | author1-link=James R. Munkres | title=Topology | publisher=[[Prentice Hall, Incorporated]] | location= | isbn=9780131816299 | year=2000}}.
 == Bibliografia ==
 * {{Citar livro|título=Curso de análise, Volume 2|ultimo=Lima|primeiro=Elon Lages|autorlink=Elon Lages Lima|data=1981|outros=Instituto de Matemática Pura e Aplicada|local=Rio de Janeiro|editora=Instituto de Matemática Pura e Aplicada|ref=harv}}
+* {{Citation | last1=Munkres | first1=James R. | author1-link=James R. Munkres | title=Topology | publisher=[[Prentice Hall, Incorporated]] | location= | isbn=9780131816299 | year=2000}}.
 {{esboço-matemática}}