将棋と上達曲線と対数則
将棋を学び始めたころは勉強すればするほど強くなったような気がしたものです。ところが、しばらくすると上達速度が落ちてきて、しまいには「かえって下手になっているんじゃないか」と悩んだり。
そのような上達の揺れについての論文『長期的技能習得データの「見晴らし台」とその意義』についての解説記事がありました。この論文は計算機科学者・翻訳者としても著名な木村泉先生※2によるもので、みそさざいという折り紙を「15万回折り続け、折るのにかかった時間がどのように変化したかを記録」したものです。
- ※1 第50回 練習の効果 | WIRED VISION
- ※2 直接お会いしたことはありませんが、今は亡き雑誌bitの記事や書籍、ジェラルド.M.ワインバーグ先生の著作の翻訳等、大変勉強させていただきました
中京大学人工知能高等研究所 IASAI NEWS No.17(PDF)表紙より
目次
上達量はかけた努力の対数になる
折り紙を折る時間がどのように短くなったかのグラフを上記WIRED VISIONの記事から孫引きします。
このグラフを見るだけでも、「時間をかければ上達する」「時々下手になることがあるが、訓練を続けるとちゃんと上達する」ことがわかります。
上達曲線はほぼ直線に見えます。他の方の論文(スキル学習におけるスランプ発生に対する事例分析的アプローチ)でもこのことは指摘されています。下図はレゴブロックを組み立てる課題の上達曲線。実際に測定された時間(水色)はほぼ直線に乗っています。
上達に必要な時間はどんどん増える
これらのグラフは両対数グラフですので、上達度が直線に乗っているということは、実は上達に必要な時間は加速度的に増えるということを意味しています。上達速度が落ちると感じるのは、気のせいではありません。
たとえば2倍上達するのに100回の練習が必要なのであれば、2×2=4倍上達するのに100×100=10000回の練習が必要だということになります。なかなか上達の道は厳しいことがわかります。
(中略)
木村氏のデータでは1万回目から2万回目までほとんど上達がみられていません。これだけスランプが続くと嫌になりそうなものですが、巾乗則を信じていたならば必ずスランプを乗り越えられると期待できたでしょうし、スランプ脱出の時期も大体予測できたから実験を続行できたのかもしれません以前の記事「強くなるためには“serious study alone”がもっとも重要」で参照した論文でも、棋力ともっとも相関の高い要素は“Total log hours serious study”(真剣な自己学習の累積時間の対数)でした。
いずれの論文でも上達はかけた時間の対数に比例すると書かれています。強くなるには遠回りのようでも地道に勉強を積み重ねるしかないようです。
下手になるのは上達する兆し
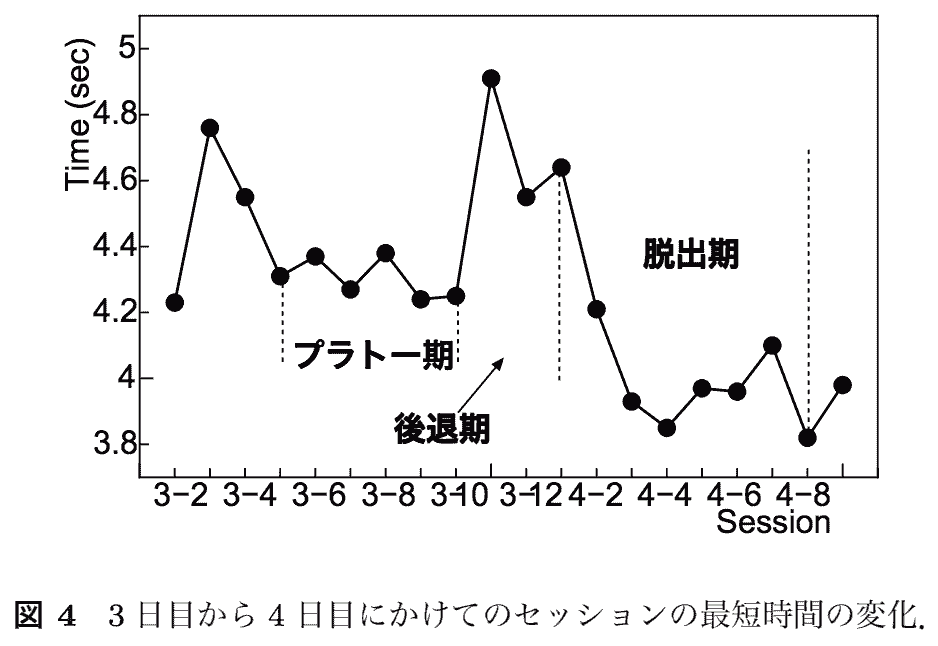
論文ではスランプが上達に欠かせないという指摘も書かれています。下図は上達する前に一時的にスランプに陥っている状態のグラフです。
この現象について論文ではこう指摘しています。
本研究では行為の微視的な分析を通して,新たに導入されたスキル(コンポーネント)がそれまでのスキルの実行環境とマッチしないこと,および実行環境を再構築する過程で混乱が生じ,その結果スランプが生じることを明らかにした。
つまり、上達するために得た能力は必ずしも今までに得た能力とは整合しないので、一時的にスランプになるわけです。例えば、将棋を始めたばかりのころは駒得することをまず覚えるべきなのですが、いつまでも駒得に拘っていては上手くなれません。どこかで駒得だけの価値観を捨てる必要があるのですが、捨てる過程では一時的に下手になるかもしれません。上達の過程でスランプに陥ることは避けられません。
これが理解できていれば、仮にスランプに陥ったとしても、それは上達の準備であると楽観できそうです。精神的にも良さそう。
参考リンク












ディスカッション
コメント一覧
素晴らしい記事です。
なんとなくわかってる事も論理的に示してもらえると支えになります。