Öz empedans

Öz direnç (Empedans), maddenin kimyasal özelliğinden dolayı direncinin artması ya da azalmasına neden olan her maddeye özgü ayırt edici bir özelliktir. Farklı maddelerin empedansları aynı olabilir ama öz dirençleri aynı olamaz. R= Lq/Q dur. (Rezistif Direnç= Uzunluk*öz direnç/kesit, (empedans ya da elektriksel empedans olarak da adlandırılır) Alternatif akım'a (İngilizce'de AC) karşı koyan zorluk olarak adlandırılır. İçinde kondansatör ve endüktans gibi zamanla değişen değerlere sahip olan elemanlar olan devrelerde direnç yerine öz direnç kullanılmaktadır. Öz direnç gerilim ve akımın sadece görünür genliğini açıklamakla kalmaz, ayrıca görünür fazını da açıklar. DA (DC) devrelerinde öz direnç ile direnç arasında hiçbir fark yoktur. Direnç sıfır faz açısına sahip öz direnç olarak adlandırılabilir.

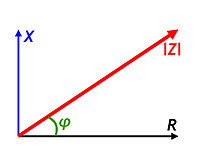
Öz direncin genellikle $\scriptstyle Z$ sembolü ile gösterilir ve hem genliğini hem de fazını ifade eden gösterim $\scriptstyle |Z|\angle \theta$ 'dir. Bununla beraber karmaşık sayı ifadesi devre analizi uygulamalarında daha sık kullanılır. Empedans (öz direnç) ifadesi ilk olarak Temmuz 1886'da Oliver Heaviside tarafından kullanıldı.^[1]^[2] 1893'te Arthur Kennelly de öz direnci karmaşık sayılarla ilk kullanandı.^[3]

Öz direnç, frekans domeninde gerilimin akıma bölümüdür. Diğer ifadeyse, gerilim–akım oranı belirli ω sıklıktaki tek bir karmaşık kuvvettir. Öz direnç genellikle karmaşık sayıdır. Fakat bu karmaşık sayı, Uluslararası Birimler Sistemi (SI)'ya göre direnç ile aynı birime sahiptir ve o da ohm'dur. Sinüzoid bir akım veya gerilim için, Karmaşık öz direncin kutupsal form, gerilim ve akımın genlik ve fazını ifade eder. Özellikle,

Karmaşık öz direncin genliği, voltaj genliğinin akımın genliğine oranıdır.
Karmaşık öz direncin fazı, akımla gerilim arasındaki faz farkıdır.

Empedansın çarpmaya göre tersi admittanstır (örn, admittans akımın gerilime oranıdır ve siemens olarak bilinir. Eskiden birimi mho idi.)

Karmaşık öz direnç

Öz direnç bir karmaşık büyüklük ile ifade edilir $\scriptstyle Z$ ve karmaşık öz direnç ifadesi de kullanılabilir. Kutupsal form hem genliği hem de faz karakteristiklerini uygun olarak karşılıyor,

\ Z=|Z|e^{i\theta }\quad

Burada $\scriptstyle |Z|$ büyüklüğü, gerilim fark genliğinin akım fark genliğine oranıdıyken, $\scriptstyle \theta$ değişkeni, gerilim ile akım arasındaki faz farkını verir ve $\scriptstyle i$ sanal kısımdır. Kartezyen formunda,

\ Z=R+iX\quad

Burada öz direncin, gerçel kısmı $\scriptstyle R$ resistans (direncini) ve sanal kısmı da $\scriptstyle X$ reaktansını verir.

Öz direnci daha uygun yapmak için kartezyen formuna ekleyip çıkartmak gerekir. Çarpma veya bölme gibi işlemlerde kutupsal form kullanılmak daha basittir. Bir devrede iki paralel öz direnç arasındaki toplam öz direnci bulmak için, hesaplamada formları birkaç kez birbirine dönüştürmek gerekebilir. Formların dönüşümü için normal karmaşık sayıların dönüşüm kuralları uygulanır.

Ohm kanunu

Bir AA devresinde

\scriptstyle Z

yüküne paralel bağlı gerilim kaynağı

\scriptstyle V

ve aynı yüke seri bağlı bir akım kaynağı

\scriptstyle I

.

Öz direncin anlamı Ohm kanununda daha iyi anlaşılabilir.^[4]^[5]

\ V=IZ=I|Z|e^{j\theta }\quad

Öz direncin büyüklüğü $\scriptstyle |Z|$ , belirli bir direnç gibidir. Belirli bir $\scriptstyle I$ akımı altında $\scriptstyle Z$ öz direncine karşı gerilimin şiddetidir. Faz faktörü, $\scriptstyle \theta$ fazına göre akımın gerilimden geri kaldığını söyler (örn, zaman domeninde akım sinyali, gerilim sinyali isteği üzerine o ana göre $\scriptstyle {\frac {\theta }{2\pi }}T$ kadar değiştirildi).^[6]

Ohm kanunlarını AA devrelerine uygulayarak öz direnç genişletilir. Gerilim bölücü, akım bölücü, Thevenin teoremi ve Norton Teoremi gibi DA (DC) devre analizindeki diğer sonuçlar da AA devrelerine, direnç yerine öz direnç konularak uygulanabilir.

Karmaşık gerilim ve akım

Bir devredeki toplam öz direnç, direnç sembolü ile aynı şekilde (US ANSI veya DIN Avro) veya etiketli bir kutu şeklinde çizilebilir.

Hesaplamaları basitleştirmek için, sinüzoidal gerilim ve akım dalgaları, yaygın olarak karmaşık değerli fonksiyonlar şu şekilde ifade edilir: $\scriptstyle V$ ve $\scriptstyle I$ .^[7]^[8]

\ V=|V|e^{j(\omega t+\phi _{V})}

\ I=|I|e^{j(\omega t+\phi _{I})}

Öz direnç, yukarıdaki niceliklerin oranı olarak tanımlanır.

\ Z={\frac {V}{I}}

Bunları Ohm kanununa uygularsak;

{\begin{aligned}|V|e^{j(\omega t+\phi _{V})}&=|I|e^{j(\omega t+\phi _{I})}|Z|e^{j\theta }\\&=|I||Z|e^{j(\omega t+\phi _{I}+\theta )}\end{aligned}}

Bu, tüm $t$ 'ler için geçerlidir. Büyüklük ve fazı şu şekilde eşitleyebiliriz:

\ |V|=|I||Z|\quad

\ \phi _{V}=\phi _{I}+\theta \quad

Büyüklük eşitliği, Ohm kanununun gerilim ve akım genliklerine uygulanmış haline benzerken ikinci eşitlik faz ilişkisini açıklar.

Karmaşık ifadenin geçerliliği

Karmaşık üs kullanılarak yukarıdaki ifade şu şekle dönüştürülebilir (Euler formülüne göre):

\ \cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}

örn, gerçek değerli sinüzoidal fonksiyon (bizim gerilim ve akım dalgasını ifade eder), iki karmaşık değerli fonksiyona ayrılabilir. Süperpozisyon ilkesine göre, sol taraftaki sinüzoidin davranışını, sağ taraftaki gibi iki karmaşık terimin davranışı gibi ayırarak analiz edebiliriz. Sadece sağ taraftaki bir terimin analizi gerçekleştirme bize diğeri için de benzer sonuç verecektir. Herhangi bir hesaplama sonunda, gerçel değerli sinüzoidleri şu ifade de yerine koyabiliriz:

\ \cos(\omega t+\phi )=\Re {\Big \{}e^{j(\omega t+\phi )}{\Big \}}

Diğer ifadeyse, basitçe sonucun gercel kısmı elde edilir.

Fazörler

Fazör, genellikle üstel formda ifade edilen sabit bir karmaşık sayıdır. Zamanın sinüzoidal fonksiyonunun karmaşık genliğini belirtir. Fazörler, sinüzoidlerin bulunduğu hesaplamaları basitleştirmek için elektrik mühendisleri tarafından kullanılırlar. Diferansiyel eşitliği cebirsel ifadeye dönüştürmek için kullanılırlar.

Bir devre elemanı olan öz direnç, fazör gerilim elemanının, fazör akım elemanına oranı olarak tanımlanabilirken ayrıca göreceli olarak gerilim ve akımın genliğini ve fazını da ifade eder. Buradaki fazör, yukarıda verilen Ohm kanunundaki $\scriptstyle e^{j\omega t}$ ifadesidir.

Aygıtsal örnekler

Eşitliklerde bobin ve kondansatörlerin öz direncinin faz açıları görülüyor. Kondansatörün gerilimi, akımını

\pi /2

kadarlık bir farkla takip ederken, bobinin gerilimi ise akımını

\pi /2

kadarlık bir farkla takip ediyor. Özdeş gerilim ve akım genlikleri, her birinin öz dirençlerinin büyüklüklerinin birbirine eşit olduğunu gösteriyor.

İdeal bir direncin empedansı tamamen gerçeldir ve rezistif empedans olarak ifade edilir:

\ Z_{R}=R.

İdeal bobinler ve kondansatörler tam sanal reaktif empedansa sahiptirler:

\ Z_{L}=j\omega L,

\ Z_{C}={\frac {1}{j\omega C}}\,.

Aşağıdaki öşdeşlikler sanal birim ve onun karşıtları içindir:

j=\cos {\left({\frac {\pi }{2}}\right)}+j\sin {\left({\frac {\pi }{2}}\right)}=e^{j{\frac {\pi }{2}}},

{\frac {1}{j}}=-j=\cos {\left(-{\frac {\pi }{2}}\right)}+j\sin {\left(-{\frac {\pi }{2}}\right)}=e^{j(-{\frac {\pi }{2}})}.

Buradan bobin ve kondansatörün empedanslarını kutupsal formda şöyle yazabiliriz:

\ Z_{L}=\omega Le^{j{\frac {\pi }{2}}},

\ Z_{C}={\frac {1}{\omega C}}e^{j(-{\frac {\pi }{2}})}.

Büyüklük, belirli bir akım genliği için, öz dirençteki, gerilimin genliğinin değişmesi, üstel faktörlerin faz ilişkisini verir.

Aygıta özgü öz direç türetme

Aşağıda, üç temel devre elemanı olan direnç, kondansatör ve bobin'in öz dirençlerinin türetilmesi gösteriliyor. Herhangi rastgele sinyalin gerilim ve akımı arasındaki ilişkiyi tanımlamak için, bu türetimlerde her rastgele sinyalin, Fourier analiziyle sinüzoidlerin toplamına yaklaşık olduğunda, sinüzoidal sinyaller varsayılacak.

Direnç

Direnç için şöyle bir ilişki vardır:

v_{\text{R}}\left(t\right)={i_{\text{R}}\left(t\right)}R.

Bu, Ohm kanununun basit ifadesidir.

Gerilim sinyaline göre,

v_{\text{R}}(t)=V_{p}\sin(\omega t)\,

olur.

Buradan

{\frac {v_{\text{R}}\left(t\right)}{i_{\text{R}}\left(t\right)}}={\frac {V_{p}\sin(\omega t)}{I_{p}\sin \left(\omega t\right)}}=R.

Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının $\scriptstyle R$ gibi bir direnç olduğunu gösteriyor ve AA gerilimini, AA akımının 0 dereceyle takip eden bir direnç olduğunu söylüyor.

Bu sonuç genellikle şu biçimde kısaltılır:

Z_{\text{direnc}}=R\,.

Kondansatör

Konsansatör için ise şöyle bir ilişki vardır:

i_{\text{C}}(t)=C{\frac {\operatorname {d} v_{\text{C}}(t)}{\operatorname {d} t}}.

Gerilim sinyaline göre

v_{\text{C}}(t)=V_{p}\sin(\omega t)\,

olur.

Buradan

{\frac {\operatorname {d} v_{\text{C}}(t)}{\operatorname {d} t}}=\omega V_{p}\cos \left(\omega t\right).

Sonrasında

{\frac {v_{\text{C}}\left(t\right)}{i_{\text{C}}\left(t\right)}}={\frac {V_{p}\sin(\omega t)}{\omega V_{p}C\cos \left(\omega t\right)}}={\frac {\sin(\omega t)}{\omega C\sin \left(\omega t+{\frac {\pi }{2}}\right)}}.

Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının $\scriptstyle {\frac {1}{\omega C}}$ gibi bir kondansatör olduğunu gösteriyor ve AA gerilimini, AA akımını -90 dereceyle takip eden bir kondansatör olduğunu söylüyor.

Bu sonuç genellikle kutupsal formda şöyle kısaltılır;

\ Z_{\text{kondansator}}={\frac {1}{\omega C}}e^{-j{\frac {\pi }{2}}}

veya Euler formülünü uygulayarak;

\ Z_{\text{kondansator}}=-j{\frac {1}{\omega C}}={\frac {1}{j\omega C}}\,.

Bobin

Bobin için şöyle ilişki vardır:

v_{\text{L}}(t)=L{\frac {\operatorname {d} i_{\text{L}}(t)}{\operatorname {d} t}}.

Bu sefer akım sinyaline göre

i_{\text{L}}(t)=I_{p}\sin(\omega t)\,,

olur

Buradan,

{\frac {\operatorname {d} i_{\text{L}}(t)}{\operatorname {d} t}}=\omega I_{p}\cos \left(\omega t\right).

Sonrasında,

{\frac {v_{\text{L}}\left(t\right)}{i_{\text{L}}\left(t\right)}}={\frac {\omega I_{p}L\cos(\omega t)}{I_{p}\sin \left(\omega t\right)}}={\frac {\omega L\sin \left(\omega t+{\frac {\pi }{2}}\right)}{\sin(\omega t)}}.

Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının $\scriptstyle \omega L$ gibi bir bobin olduğunu gösteriyor ve AA gerilimini, AA akımını 90 dereceyle takip eden bir bobin olduğunu söylüyor.

Bu sonuç kutupsal forma genellikle şöyle kısaltılabilir; : $\ Z_{\text{bobin}}=\omega Le^{j{\frac {\pi }{2}}}.$

Veya daha basit olarak Euler formülü kullanılarak; : $\ Z_{\text{bobin}}=j\omega L.\,$

Resistans ve reaktans

Direnç ve reaktans öz direncin genlik ve fazını birlikte şu şekilde ifade ederler:

|Z|={\sqrt {ZZ^{*}}}={\sqrt {R^{2}+X^{2}}}

\theta =\arctan {\left({\frac {X}{R}}\right)}

Birçok uygulamada gerilim ve akımın göreceli fazı, çok da önemli olmadığında, sadece öz direncin genliği önemlidir.

Direnç

Direnç $\scriptstyle R$ öz direncin gercel kısmıdır. Tam rezistif empedanslı bir aygıtta, akım ve gerilim arasında faz farkı yoktur.

\ R=|Z|\cos {\theta }\quad

Reaktans

Reaktans $\scriptstyle X$ , öz direncin sanal kısmını ifade eder. Sonlu reaktansa sahip bir bileşenin, akımı ile gerilimi arasında $\scriptstyle \theta$ kadar bir faz farkı vardır.

\ X=|Z|\sin {\theta }\quad

Tam reaktif bileşeninde, sinüzoidal gerilim, akımın tam çeyrek evre farkladır. Bu, bileşenin, devredeki enerjiyi çektiği ve sonra tekrar devreye geri verdiği anlamına gelir Saf reaktans hiçbir güç harcamaz.

Kapasitif reaktans

Kondansatör tam reaktif empedansa sahiptir, o da sinyal frekansı ile ters orantılıdır. Kondansatör, bir yalıtkanla (dielektrik olarak da bilinir) ayrılan iki iletkenden oluşur.

Düşük frekanslarda kondansatör açık devredir ve yalıtkandan akan yük yoktur...

İndüktif reaktans

İndüktif reaktans $\scriptstyle {X_{L}}$ , sinyal frekanslı $\scriptstyle {f}$ ve indüktans $\scriptstyle {L}$ ile orantılıdır.

X_{L}=\omega L=2\pi fL\quad

Bobin iletken sargılardan oluşur. Elektromanyetik indükleme, Faraday yasasına göre, $\scriptstyle {B}$ manyetik alanının yük miktarından dolayı bir akım çevriminde, $\scriptstyle {\mathcal {E}}$ emk'sını geri verir (akıma karşı gerilim)

{\mathcal {E}}=-{{d\Phi _{B}} \over dt}\quad

$N$ sarımlı bir bobindeki emk;

{\mathcal {E}}=-N{d\Phi _{B} \over dt}\quad

Geri emk, akan akımın karşısındaki kaynaktır. Sabit doğru akımda sıfır yük vardır ve bobin kısa devre gibi gözükür. Alternatif akım ortalama bir zamanda yüke sahiptir ve frekansla orantılıdır. Bundan dolayıdır ki indüktif reaktans frekansla artar.

Ayrıca bakınız

Empedans kontrolü

Kaynakça

^ Science, p. 18, 1888
^ Oliver Heaviside, Elektrikçi, p. 212, 23 Temmuz 1886'da Elektriksel sayfalara yazıldı, p64, AMS Bookstore, ISBN 0-8218-3465-7
^ Kennelly, Arthur. Öz direnç (IEEE, 1893)
^ AC Ohm's law 19 Şubat 2011 tarihinde Wayback Machine sitesinde arşivlendi., Hyperphysics
^ Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 32-33. ISBN 0-521-37095-7.
^ Capacitor/inductor phase relationships 3 Ağustos 2008 tarihinde Wayback Machine sitesinde arşivlendi., Yokogawa
^ Complex impedance 19 Temmuz 2010 tarihinde Wayback Machine sitesinde arşivlendi., Hyperphysics
^ Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 31-32. ISBN 0-521-37095-7.

[1] Science, p. 18, 1888

[2] Oliver Heaviside, Elektrikçi, p. 212, 23 Temmuz 1886'da Elektriksel sayfalara yazıldı, p64, AMS Bookstore, ISBN 0-8218-3465-7

[3] Kennelly, Arthur. Öz direnç (IEEE, 1893)

[4] AC Ohm's law 19 Şubat 2011 tarihinde Wayback Machine sitesinde arşivlendi., Hyperphysics

[HH1-5] Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 32-33. ISBN 0-521-37095-7.

[6] Capacitor/inductor phase relationships 3 Ağustos 2008 tarihinde Wayback Machine sitesinde arşivlendi., Yokogawa

[7] Complex impedance 19 Temmuz 2010 tarihinde Wayback Machine sitesinde arşivlendi., Hyperphysics

[HH2-8] Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 31-32. ISBN 0-521-37095-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]