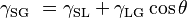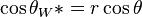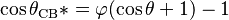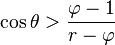Hydrophobe

For other uses, see Hydrophobia (disambiguation).

165 degree water contact angle on a surface modified using plasma technology system surface chemistry. The contact angle is the red angle plus 90 degrees.

Dew drop on a hydrophobic leaf surface

Cutting a water droplet using a superhydrophobic knife on superhydrophobic surfaces

Water drops on the hydrophobic surface of grass

In chemistry, hydrophobicity is the physical property of a molecule (known as a hydrophobe) that is seemingly repelled from a mass of water. (Strictly speaking, there is no repulsive force involved; it is an absence of attraction.)

Hydrophobic molecules tend to be non-polar and, thus, prefer other neutral molecules and non-polar solvents. Hydrophobic molecules in water often cluster together, forming micelles. Water on hydrophobic surfaces will exhibit a high contact angle.

Examples of hydrophobic molecules include the alkanes, oils, fats, and greasy substances in general. Hydrophobic materials are used for oil removal from water, the management of oil spills, and chemical separation processes to remove non-polar substances from polar compounds.

Hydrophobic is often used interchangeably with lipophilic, "fat-loving." However, the two terms are not synonymous. While hydrophobic substances are usually lipophilic, there are exceptions—such as the silicones and fluorocarbons.

The term hydrophobe comes from the Ancient Greek ὑδρόφοβος, "having a horror of water", constructed from ὕδωρ, "water", and φόβος, "fear".

Chemical background

Main article: Hydrophobic force

The hydrophobic interaction is mostly an entropic effect originating from the disruption of the highly dynamic hydrogen bonds between molecules of liquid water by the nonpolar solute forming a clathrate-like structure around the non-polar molecules. This structure formed is more highly ordered than free water molecules due to the water molecules arranging themselves to interact as much as possible with themselves, and thus results in a higher entropic state which causes non-polar molecules to clump together to reduce the surface area exposed to water and decrease the entropy of the system. Thus, the two immiscible phases (hydrophilic vs. hydrophobic) will change so that their corresponding interfacial area will be minimal. This effect can be visualized in the phenomenon called phase separation.

Superhydrophobicity

Main article: Superhydrophobe

A water drop on a Lotus plant leaf.

Superhydrophobic surfaces, such as the leaves of the lotus plant, are those that are extremely difficult to wet. The contact angles of a water droplet exceeds 150° and the roll-off angle is less than 10°. This is referred to as the Lotus effect, and is primarily a physical property related to interfacial tension, rather than a chemical property.

Theory

In 1805, Thomas Young defined the contact angle θ by analyzing the forces acting on a fluid droplet resting on a solid surface surrounded by a gas.

A liquid droplet rests on a solid surface and is surrounded by gas. The contact angle, θ_C, is the angle formed by a liquid at the three-phase boundary where the liquid, gas, and solid intersect.

A droplet resting on a solid surface and surrounded by a gas forms a characteristic contact angle θ. If the solid surface is rough, and the liquid is in intimate contact with the solid asperities, the droplet is in the Wenzel state. If the liquid rests on the tops of the asperities, it is in the Cassie–Baxter state.

$\gamma_\text{SG}\ =\gamma_\text{SL}+\gamma_\text{LG}\cos{\theta} \,$

where

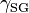$\gamma_\text{SG}\$ = Interfacial tension between the solid and gas

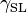$\gamma_\text{SL}\$ = Interfacial tension between the solid and liquid

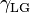$\gamma_\text{LG}\$ = Interfacial tension between the liquid and gas

θ can be measured using a contact angle goniometer.

Wenzel determined that when the liquid is in intimate contact with a microstructured surface, θ will change to θ_W*

$\cos{\theta}_W* = r \cos{\theta} \,$

where r is the ratio of the actual area to the projected area. Wenzel's equation shows that microstructuring a surface amplifies the natural tendency of the surface. A hydrophobic surface (one that has an original contact angle greater than 90°) becomes more hydrophobic when microstructured – its new contact angle becomes greater than the original. However, a hydrophilic surface (one that has an original contact angle less than 90°) becomes more hydrophilic when microstructured – its new contact angle becomes less than the original. Cassie and Baxter found that if the liquid is suspended on the tops of microstructures, θ will change to θ_CB*:

$\cos{\theta}_\text{CB}* = \varphi(\cos\theta + 1) - 1 \,$

where φ is the area fraction of the solid that touches the liquid. Liquid in the Cassie–Baxter state is more mobile than in the Wenzel state.

We can predict whether the Wenzel or Cassie–Baxter state should exist by calculating the new contact angle with both equations. By a minimization of free energy argument, the relation that predicted the smaller new contact angle is the state most likely to exist. Stated in mathematical terms, for the Cassie–Baxter state to exist, the following inequality must be true.

$\cos\theta>\frac{\varphi-1}{r-\varphi}$

A recent alternative criterion for the Cassie–Baxter state asserts that the Cassie–Baxter state exists when the following 2 criteria are met: 1) Contact line forces overcome body forces of unsupported droplet weight and 2) The microstructures are tall enough to prevent the liquid that bridges microstructures from touching the base of the microstructures.

A new criterion for the switch between Wenzel and Cassie-Baxter states has been developed recently based on surface roughness and surface energy. The criterion focuses on the air-trapping capability under liquid droplets on rough surfaces, which could tell whether Wenzel's model or Cassie-Baxter's model should be used for certain combination of surface roughness and energy.

Contact angle is a measure of static hydrophobicity, and contact angle hysteresis and slide angle are dynamic measures. Contact angle hysteresis is a phenomenon that characterizes surface heterogeneity. When a pipette injects a liquid onto a solid, the liquid will form some contact angle. As the pipette injects more liquid, the droplet will increase in volume, the contact angle will increase, but its three-phase boundary will remain stationary until it suddenly advances outward. The contact angle the droplet had immediately before advancing outward is termed the advancing contact angle. The receding contact angle is now measured by pumping the liquid back out of the droplet. The droplet will decrease in volume, the contact angle will decrease, but its three-phase boundary will remain stationary until it suddenly recedes inward. The contact angle the droplet had immediately before receding inward is termed the receding contact angle. The difference between advancing and receding contact angles is termed contact angle hysteresis and can be used to characterize surface heterogeneity, roughness, and mobility. Surfaces that are not homogeneous will have domains that impede motion of the contact line.The slide angle is another dynamic measure of hydrophobicity and is measured by depositing a droplet on a surface and tilting the surface until the droplet begins to slide. In general, liquids in the Cassie–Baxter state exhibit lower slide angles and contact angle hysteresis than those in the Wenzel state.

Research and development

Water droplets roll down an inclined hydrophobic surface.

Water droplets on an artificial hydrophobic surface (left)

Dettre and Johnson discovered in 1964 that the superhydrophobic, Lotus effect phenomenon was related to rough hydrophobic surfaces, and they developed a theoretical model based on experiments with glass beads coated with paraffin or TFE telomer. The self-cleaning property of superhydrophobic micro-nanostructured surfaces was reported in 1977. Perfluoroalkyl, perfluoropolyether and RF plasma formed superhydrophobic materials were developed, used for electrowetting and commercialized for bio-medical applications between 1986 and 1995. Other technology and applications have emerged since the mid 1990s. A durable superhydrophobic hierarchical composition, applied in one or two steps, was disclosed in 2002 comprising nano-sized particles ≤ 100 nanometers overlaying a surface having micrometer-sized features or particles ≤ 100 micrometers. The larger particles were observed to protect the smaller particles from mechanical abrasion.

In recent research, superhydrophobicity has been reported by allowing alkylketene dimer (AKD) to solidify into a nanostructured fractal surface. Many papers have since presented fabrication methods for producing superhydrophobic surfaces including particle deposition, sol-gel techniques, plasma treatments, vapor deposition, and casting techniques. Current opportunity for research impact lies mainly in fundamental research and practical manufacturing. Debates have recently emerged concerning the applicability of the Wenzel and Cassie–Baxter models. In an experiment designed to challenge the surface energy perspective of the Wenzel and Cassie–Baxter model and promote a contact line perspective, water drops were placed on a smooth hydrophobic spot in a rough hydrophobic field, a rough hydrophobic spot in a smooth hydrophobic field, and a hydrophilic spot in a hydrophobic field. Experiments showed that the surface chemistry and geometry at the contact line affected the contact angle and contact angle hysteresis, but the surface area inside the contact line had no effect. An argument that increased jaggedness in the contact line enhances droplet mobility has also been proposed.

Many very hydrophobic materials found in nature rely on Cassie's law and are biphasic on the submicrometer level with one component air. The Lotus effect is based on this principle. Inspired by it, a lot of functional superhydrophobic surfaces were prepared.

An example of a biomimetic superhydrophobic material in nanotechnology is nanopin film. In one study, a vanadium pentoxide surface that can switch reversibly between superhydrophobicity and superhydrophilicity under the influence of UV radiation is presented. According to the study, any surface can be modified to this effect by application of a suspension of rose-like V₂O₅ particles, for instance with an inkjet printer. Once again hydrophobicity is induced by interlaminar air pockets (separated by 2.1 nm distances). The UV effect is also explained. UV light creates electron-hole pairs, with the holes reacting with lattice oxygen, creating surface oxygen vacancies, while the electrons reduce V⁵⁺ to V³⁺. The oxygen vacancies are met by water, and it is this water absorbency by the vanadium surface that makes it hydrophilic. By extended storage in the dark, water is replaced by oxygen and hydrophilicity is once again lost.

Potential applications

Active recent research on superhydrophobic materials might eventually lead to industrial applications. For example, a simple routine of coating cotton fabric with silica or titania particles by sol-gel technique has been reported, which protects the fabric from UV light and makes it superhydrophobic. Also, an efficient routine has been reported for making polyethylene superhydrophobic and thus self-cleaning.—99% of dirt absorbed on such surface is easily washed away. Patterned superhydrophobic surfaces also have promise for lab-on-a-chip microfluidic devices and can drastically improve surface-based bioanalysis.

See also

• Amphiphile
• Froth flotation
• Hydrophile
• Hydrophobic effect
• Hydrophobicity scales
• Superhydrophobe
• Superhydrophobic coating
• Silicon organic water repellent