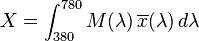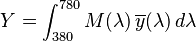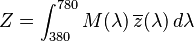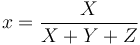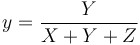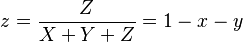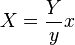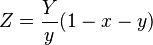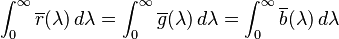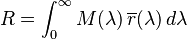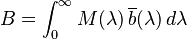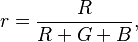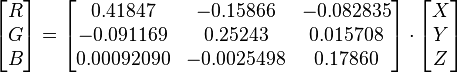CIE 1931 color space
The CIE 1931 colour spaces are the first defined quantitative links between physical pure colours (i.e. wavelengths) in the electromagnetic visible spectrum, and physiological perceived colours in human colour vision. The mathematical relationships that define these colour spaces are essential tools for colour management. They allow one to translate different physical responses to visible radiation in colour inks, illuminated displays, and recording devices such as digital cameras into a universal human colour vision response. CIE 1931 RGB colour space and CIE 1931 XYZ colour space were created by the International Commission on Illumination (CIE) in 1931.[1][2] The CIE XYZ colour space was derived from a series of experiments done in the late 1920s by William David Wright[3] and John Guild.[4] Their experimental results were combined into the specification of the CIE RGB colour space, from which the CIE XYZ colour space was derived.
Contents
Tristimulus values

The human eye with normal vision has three kinds of cone cells, which sense light, with spectral sensitivity peaks in short (S, 420–440 nm), middle (M, 530–540 nm), and long (L, 560–580 nm) wavelengths. These cone cells underlie human colour perception under medium- and high-brightness conditions (in very dim light, colour vision diminishes, and the low-brightness, monochromatic "night-vision" receptors, called rod cells, take over). Thus, three parameters, corresponding to levels of stimulus of the three types of cone cells, can in principle describe any colour sensation. Weighting a total light power spectrum by the individual spectral sensitivities of the three types of cone cells gives three effective stimulus values; these three values make up a tristimulus specification of the objective colour of the light spectrum. The three parameters, denoted S, M, and L, can be indicated using a 3-dimensional space, called LMS colour space, which is one of many colour spaces which have been devised to help quantify human colour vision.
A colour space maps a range of physically produced colours (from mixed light, pigments, etc.) to an objective description of colour sensations registered in the eye, typically in terms of tristimulus values, but not usually in the LMS space defined by the cone spectral sensitivities. The tristimulus values associated with a colour space can be conceptualized as amounts of three primary colours in a tri-chromatic additive colour model. In some colour spaces, including LMS and XYZ spaces, the primary colours used are not real colours, in the sense that they cannot be generated with any light spectrum.
The CIE XYZ colour space encompasses all colour sensations that an average person can experience. That is why CIE XYZ (Tristimulus values) is a device invariant colour representation.[5] It serves as a standard reference against which many other colour spaces are defined. A set of colour-matching functions, like the spectral sensitivity curves of the LMS space but not restricted to be nonnegative sensitivities, associates physically produced light spectra with specific tristimulus values.
Consider two light sources made up of different mixtures of various wavelengths. Such light sources may appear to be the same colour; this effect is called metamerism. Such light sources have the same apparent colour to an observer when they produce the same tristimulus values, no matter what the spectral power distributions of the sources are.
Most wavelengths stimulate two or all three types of cone cell, because the spectral sensitivity curves of the three types of cone cells overlap. Certain tristimulus values are thus physically impossible (for instance LMS tristimulus values that are non-zero for the M component, and zero for both L and S). And LMS tristimulus values for pure spectral colours would, in any normal trichromatic additive colour space (e.g. RGB colour spaces), imply negative values for at least one of the three primaries, since the chromaticity would be outside the colour triangle defined by the primary colours. To avoid these negative RGB values, and to have one component that describes the perceived brightness, "imaginary" primary colours and corresponding colour-matching functions have been formulated. The resulting tristimulus values are defined by the CIE 1931 colour space, in which they are denoted X, Y, and Z.[6] In XYZ space, all combinations of nonnegative coordinates are meaningful, but many such as the primary locations [1, 0, 0], [0, 1, 0], and [0, 0, 1] correspond to imaginary colours outside the space of possible LMS coordinates; imaginary colours do not correspond to any spectral distribution of wavelengths, so have no physical reality.
Meaning of X, Y, and Z
Lua error in package.lua at line 80: module 'strict' not found.

When judging the relative luminance (brightness) of different colours in well-lit situations, humans tend to perceive light within the green parts of the spectrum as brighter than red or blue light of equal power. The luminosity function that describes the perceived brightnesses of different wavelengths is thus roughly analogous to the spectral sensitivity of M cones.
The CIE model capitalises on this fact by defining Y as luminance. Z is quasi-equal to blue stimulation, or the S cone response, and X is a mix (a linear combination) of cone response curves chosen to be nonnegative. The XYZ tristimulus values are thus analogous to, but different from, the LMS cone responses of the human eye. Defining Y as luminance has the useful result that for any given Y value, the XZ plane will contain all possible chromaticities at that luminance.
CIE standard observer
Due to the distribution of cones in the eye, the tristimulus values depend on the observer's field of view. To eliminate this variable, the CIE defined a colour-mapping function called the standard (colourimetric) observer, to represent an average human's chromatic response within a 2° arc inside the fovea. This angle was chosen owing to the belief that the colour-sensitive cones resided within a 2° arc of the fovea. Thus the CIE 1931 Standard Observer function is also known as the CIE 1931 2° Standard Observer. A more modern but less-used alternative is the CIE 1964 10° Standard Observer, which is derived from the work of Stiles and Burch,[7] and Speranskaya.[8]
For the 10° experiments, the observers were instructed to ignore the central 2° spot. The 1964 Supplementary Standard Observer function is recommended when dealing with more than about a 4° field of view. Both standard observer functions are discretized at 5 nm wavelength intervals from 380 nm to 780 nm and distributed by the CIE.[9] All corresponding values have been calculated from experimentally obtained data using interpolation. The standard observer is characterized by three colour matching functions.
The derivation of the CIE standard observer from colour matching experiments is given below, after the description of the CIE RGB space.
colour matching functions
The CIE's colour matching functions 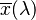 ,
, 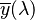 and
and 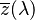 are the numerical description of the chromatic response of the observer (described above). They can be thought of as the spectral sensitivity curves of three linear light detectors yielding the CIE tristimulus values X, Y and Z. Collectively, these three functions are known as the CIE standard observer.[10]
are the numerical description of the chromatic response of the observer (described above). They can be thought of as the spectral sensitivity curves of three linear light detectors yielding the CIE tristimulus values X, Y and Z. Collectively, these three functions are known as the CIE standard observer.[10]
The tristimulus values for a colour with a spectral power distribution 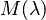 are given in terms of the standard observer by:
are given in terms of the standard observer by:
where 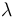 is the wavelength of the equivalent monochromatic light (measured in nanometers).
is the wavelength of the equivalent monochromatic light (measured in nanometers).
Other observers, such as for the CIE RGB space or other RGB colour spaces, are defined by other sets of three colour-matching functions, and lead to tristimulus values in those other spaces.
The values of X, Y, and Z are bounded if the intensity spectrum 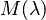 is bounded.
is bounded.
CIE xy chromaticity diagram and the CIE xyY colour space
Lua error in package.lua at line 80: module 'strict' not found.


Since the human eye has three types of colour sensors that respond to different ranges of wavelengths, a full plot of all visible colours is a three-dimensional figure. However, the concept of colour can be divided into two parts: brightness and chromaticity. For example, the colour white is a bright colour, while the colour grey is considered to be a less bright version of that same white. In other words, the chromaticity of white and grey are the same while their brightness differs.
The CIE XYZ colour space was deliberately designed so that the Y parameter was a measure of the brightness or luminance of a colour. The chromaticity of a colour was then specified by the two derived parameters x and y, two of the three normalized values which are functions of all three tristimulus values X, Y, and Z:
The derived colour space specified by x, y, and Y is known as the CIE xyY colour space and is widely used to specify colours in practice.
The X and Z tristimulus values can be calculated back from the chromaticity values x and y and the Y tristimulus value:
The figure on the right shows the related chromaticity diagram. The outer curved boundary is the spectral locus, with wavelengths shown in nanometers. Note that the chromaticity diagram is a tool to specify how the human eye will experience light with a given spectrum. It cannot specify colours of objects (or printing inks), since the chromaticity observed while looking at an object depends on the light source as well.
Mathematically, x and y are projective coordinates and the colours of the chromaticity diagram occupy a region of the real projective plane.
The chromaticity diagram illustrates a number of interesting properties of the CIE XYZ colour space:
- The diagram represents all of the chromaticities visible to the average person. These are shown in colour and this region is called the gamut of human vision. The gamut of all visible chromaticities on the CIE plot is the tongue-shaped or horseshoe-shaped figure shown in colour. The curved edge of the gamut is called the spectral locus and corresponds to monochromatic light (each point representing a pure hue of a single wavelength), with wavelengths listed in nanometers. The straight edge on the lower part of the gamut is called the line of purples. These colours, although they are on the border of the gamut, have no counterpart in monochromatic light. Less saturated colours appear in the interior of the figure with white at the center.
- It is seen that all visible chromaticities correspond to non-negative values of x, y, and z (and therefore to non-negative values of X, Y, and Z).
- If one chooses any two points of colour on the chromaticity diagram, then all the colours that lie in a straight line between the two points can be formed by mixing these two colours. It follows that the gamut of colours must be convex in shape. All colours that can be formed by mixing three sources are found inside the triangle formed by the source points on the chromaticity diagram (and so on for multiple sources).
- An equal mixture of two equally bright colours will not generally lie on the midpoint of that line segment. In more general terms, a distance on the xy chromaticity diagram does not correspond to the degree of difference between two colours. In the early 1940s, David MacAdam studied the nature of visual sensitivity to colour differences, and summarized his results in the concept of a MacAdam ellipse. Based on the work of MacAdam, the CIE 1960, CIE 1964, and CIE 1976 colour spaces were developed, with the goal of achieving perceptual uniformity (have an equal distance in the colour space correspond to equal differences in colour). Although they were a distinct improvement over the CIE 1931 system, they were not completely free of distortion.
- It can be seen that, given three real sources, these sources cannot cover the gamut of human vision. Geometrically stated, there are no three points within the gamut that form a triangle that includes the entire gamut; or more simply, the gamut of human vision is not a triangle.
- Light with a flat power spectrum in terms of wavelength (equal power in every 1 nm interval) corresponds to the point (x,y) = (1/3,1/3).
Definition of the CIE XYZ colour space
CIE RGB colour space
The CIE RGB colour space is one of many RGB colour spaces, distinguished by a particular set of monochromatic (single-wavelength) primary colours.
In the 1920s, W. David Wright[3] and John Guild[4] independently conducted a series of experiments on human sight which laid the foundation for the specification of the CIE XYZ colour space. Wright carried out trichromatic colour matching experiments with ten observers. Guild actually conducted his experiments with seven observers.
The experiments were conducted by using a circular split screen (a bipartite field) 2 degrees in diameter, which is the angular size of the human fovea. On one side of the field a test colour was projected and on the other side, an observer-adjustable colour was projected. The adjustable colour was a mixture of three primary colours, each with fixed chromaticity, but with adjustable brightness.
The observer would alter the brightness of each of the three primary beams until a match to the test colour was observed. Not all test colours could be matched using this technique. When this was the case, a variable amount of one of the primaries could be added to the test colour, and a match with the remaining two primaries was carried out with the variable colour spot. For these cases, the amount of the primary added to the test colour was considered to be a negative value. In this way, the entire range of human colour perception could be covered. When the test colours were monochromatic, a plot could be made of the amount of each primary used as a function of the wavelength of the test colour. These three functions are called the colour matching functions for that particular experiment.
Although Wright and Guild's experiments were carried out using various primaries at various intensities, and although they used a number of different observers, all of their results were summarized by the standardized CIE RGB colour matching functions  ,
, 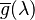 , and
, and 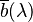 , obtained using three monochromatic primaries at standardized wavelengths of 700 nm (red), 546.1 nm (green) and 435.8 nm (blue). The colour matching functions are the amounts of primaries needed to match the monochromatic test primary. These functions are shown in the plot on the right (CIE 1931). Note that
, obtained using three monochromatic primaries at standardized wavelengths of 700 nm (red), 546.1 nm (green) and 435.8 nm (blue). The colour matching functions are the amounts of primaries needed to match the monochromatic test primary. These functions are shown in the plot on the right (CIE 1931). Note that  and
and 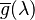 are zero at 435.8,
are zero at 435.8,  and
and 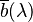 are zero at 546.1 and
are zero at 546.1 and 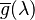 and
and 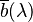 are zero at 700 nm, since in these cases the test colour is one of the primaries. The primaries with wavelengths 546.1 nm and 435.8 nm were chosen because they are easily reproducible monochromatic lines of a mercury vapor discharge. The 700 nm wavelength, which in 1931 was difficult to reproduce as a monochromatic beam, was chosen because the eye's perception of colour is rather unchanging at this wavelength, and therefore small errors in wavelength of this primary would have little effect on the results.
are zero at 700 nm, since in these cases the test colour is one of the primaries. The primaries with wavelengths 546.1 nm and 435.8 nm were chosen because they are easily reproducible monochromatic lines of a mercury vapor discharge. The 700 nm wavelength, which in 1931 was difficult to reproduce as a monochromatic beam, was chosen because the eye's perception of colour is rather unchanging at this wavelength, and therefore small errors in wavelength of this primary would have little effect on the results.
The colour matching functions and primaries were settled upon by a CIE special commission after considerable deliberation.[11] The cut-offs at the short- and long-wavelength side of the diagram are chosen somewhat arbitrarily; the human eye can actually see light with wavelengths up to about 810 nm, but with a sensitivity that is many thousand times lower than for green light. These colour matching functions define what is known as the "1931 CIE standard observer". Note that rather than specify the brightness of each primary, the curves are normalized to have constant area beneath them. This area is fixed to a particular value by specifying that
The resulting normalized colour matching functions are then scaled in the r:g:b ratio of 1:4.5907:0.0601 for source luminance and 72.0962:1.3791:1 for source radiant power to reproduce the true colour matching functions. By proposing that the primaries be standardized, the CIE established an international system of objective colour notation.
Given these scaled colour matching functions, the RGB tristimulus values for a colour with a spectral power distribution 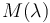 would then be given by:
would then be given by:
These are all inner products and can be thought of as a projection of an infinite-dimensional spectrum to a three-dimensional colour. (See also: Hilbert space)
Grassmann's law
One might ask: "Why is it possible that Wright and Guild's results can be summarized using different primaries and different intensities from those actually used?" One might also ask: "What about the case when the test colours being matched are not monochromatic?" The answer to both of these questions lies in the (near) linearity of human colour perception. This linearity is expressed in Grassmann's law.
The CIE RGB space can be used to define chromaticity in the usual way: The chromaticity coordinates are r and g where:
Construction of the CIE XYZ colour space from the Wright–Guild data
Having developed an RGB model of human vision using the CIE RGB matching functions, the members of the special commission wished to develop another colour space that would relate to the CIE RGB colour space. It was assumed that Grassmann's law held, and the new space would be related to the CIE RGB space by a linear transformation. The new space would be defined in terms of three new colour matching functions 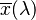 ,
, 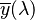 , and
, and 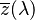 as described above. The new colour space would be chosen to have the following desirable properties:
as described above. The new colour space would be chosen to have the following desirable properties:

- The new colour matching functions were to be everywhere greater than or equal to zero. In 1931, computations were done by hand or slide rule, and the specification of positive values was a useful computational simplification.
- The
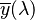 colour matching function would be exactly equal to the photopic luminous efficiency function V(λ) for the "CIE standard photopic observer".[12] The luminance function describes the variation of perceived brightness with wavelength. The fact that the luminance function could be constructed by a linear combination of the RGB colour matching functions was not guaranteed by any means but might be expected to be nearly true due to the near-linear nature of human sight. Again, the main reason for this requirement was computational simplification.
colour matching function would be exactly equal to the photopic luminous efficiency function V(λ) for the "CIE standard photopic observer".[12] The luminance function describes the variation of perceived brightness with wavelength. The fact that the luminance function could be constructed by a linear combination of the RGB colour matching functions was not guaranteed by any means but might be expected to be nearly true due to the near-linear nature of human sight. Again, the main reason for this requirement was computational simplification. - For the constant energy white point, it was required that x = y = z = 1/3.
- By virtue of the definition of chromaticity and the requirement of positive values of x and y, it can be seen that the gamut of all colours will lie inside the triangle [1,0], [0,0], [0,1]. It was required that the gamut fill this space practically completely.
- It was found that the
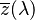 colour matching function could be set to zero above 650 nm while remaining within the bounds of experimental error. For computational simplicity, it was specified that this would be so.
colour matching function could be set to zero above 650 nm while remaining within the bounds of experimental error. For computational simplicity, it was specified that this would be so.
In geometrical terms, choosing the new colour space amounts to choosing a new triangle in rg chromaticity space. In the figure above-right, the rg chromaticity coordinates are shown on the two axes in black, along with the gamut of the 1931 standard observer. Shown in red are the CIE xy chromaticity axes which were determined by the above requirements. The requirement that the XYZ coordinates be non-negative means that the triangle formed by Cr, Cg, Cb must encompass the entire gamut of the standard observer. The line connecting Cr and Cb is fixed by the requirement that the 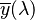 function be equal to the luminance function. This line is the line of zero luminance, and is called the alychne. The requirement that the
function be equal to the luminance function. This line is the line of zero luminance, and is called the alychne. The requirement that the 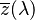 function be zero above 650 nm means that the line connecting Cg and Cr must be tangent to the gamut in the region of Kr. This defines the location of point Cr. The requirement that the equal energy point be defined by x = y = 1/3 puts a restriction on the line joining Cb and Cg, and finally, the requirement that the gamut fill the space puts a second restriction on this line to be very close to the gamut in the green region, which specifies the location of Cg and Cb. The above described transformation is a linear transformation from the CIE RGB space to XYZ space. The standardized transformation settled upon by the CIE special commission was as follows:
function be zero above 650 nm means that the line connecting Cg and Cr must be tangent to the gamut in the region of Kr. This defines the location of point Cr. The requirement that the equal energy point be defined by x = y = 1/3 puts a restriction on the line joining Cb and Cg, and finally, the requirement that the gamut fill the space puts a second restriction on this line to be very close to the gamut in the green region, which specifies the location of Cg and Cb. The above described transformation is a linear transformation from the CIE RGB space to XYZ space. The standardized transformation settled upon by the CIE special commission was as follows:
The numbers in the conversion matrix below are exact, with the number of digits specified in CIE standards.[11]
While the above matrix is exactly specified in standards, going the other direction uses an inverse matrix that is not exactly specified, but is approximately:
The integrals of the XYZ colour matching functions must all be equal by requirement 3 above, and this is set by the integral of the photopic luminous efficiency function by requirement 2 above. The tabulated sensitivity curves have a certain amount of arbitrariness in them. The shapes of the individual X, Y and Z sensitivity curves can be measured with a reasonable accuracy. However, the overall luminosity curve (which in fact is a weighted sum of these three curves) is subjective, since it involves asking a test person whether two light sources have the same brightness, even if they are in completely different colours. Along the same lines, the relative magnitudes of the X, Y, and Z curves are arbitrary. Furthermore, one could define a valid colour space with an X sensitivity curve that has twice the amplitude. This new colour space would have a different shape. The sensitivity curves in the CIE 1931 and 1964 XYZ colour spaces are scaled to have equal areas under the curves.
See also
- Trichromacy
- Imaginary colour
- Lab colour space
- Standard illuminant, the definition of white point used by CIE and commonly shown in colour space diagrams as E, D50 or D65
References
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 3.0 3.1 Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 4.0 4.1 Lua error in package.lua at line 80: module 'strict' not found.
- ↑ [1] Tristimulus Value of Color : Device Independent Color Representation
- ↑ Lua error in package.lua at line 80: module 'strict' not found.. See pgs. 39–46 for the basis in human eye physiology of three-component color models, and 54–57 for chromaticity coordinates.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 11.0 11.1 Lua error in package.lua at line 80: module 'strict' not found. and Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found. Note that the 1924 luminous efficiency function seriously underestimates sensitivity at wavelengths below 460 nm, and has been supplemented with newer and more accurate luminosity curves; see Luminosity function#Improvements to the standard.
Further reading
- Lua error in package.lua at line 80: module 'strict' not found.
- Lua error in package.lua at line 80: module 'strict' not found.
- Lua error in package.lua at line 80: module 'strict' not found. (originally published by the Society of Dyers and Colourists, Bradford, 1981.)
External links
- Introduction to Colour Science, William Andrew Steer.
- efg's colour Chromaticity Diagrams Lab Report and Delphi source
- CIE colour Space, Gernot Hoffmann
- Annotated downloadable data tables, Andrew Stockman and Lindsay T. Sharpe.
- Calculation from the original experimental data of the CIE 1931 RGB standard observer spectral chromaticity co-ordinates and colour matching functions
- colourimetric data useful for calculation, in various file formats
- colourLAB MATLAB toolbox for colour science computation and accurate colour reproduction. It includes CIE standard tristimulus colourimetry and transformations to a number of non-linear colour appearance models (CIE Lab, CIE CAM, etc.).
- Precise colour Communication Konica Minolta Sensing
- CIE 1931 and LED Binning Explained, Edaphic Scientific Knowledge Base