たのしい高階関数

こわくないよ

たのしい高階関数
λ
発表をする
▲

資料をつくる
資料をあきらめる

たのしい高階関数 λ 　

目的
本勉強会の趣旨

本セッションは高階関数入門です
関数型言語の視野を拡げ、たのしく
使っていくことを目的としております。

大事なことなので
２回いいました


注意事項


関数型言語は怖いイメージがあるみたいですが


当セッションはイージーモードです。


モナド / ファンクタ / 遅延評価 / 圏論 / 論証

ダメ。ゼッタイ。
「みんなやってる」なんて理由にならない

プログラマたちは　ぜんめつしました。

このような悲劇を繰り返さないためにもね

たのしく
学びましょう～


自己紹介
Java ★★☆
Scala ☆☆☆
Haskell ☆☆☆

そろそろ Scala で仕事したいです。

アストルティア
Twitter@s_kozake


Agenda
高階関数ってなに？

高階関数を学ぶメリット

リストを扱う高階関数

まとめ



引数として関数を取ったり、
返り値として関数を返したりする関数

関数型言語では、
関数がファーストクラスオブジェクト
として扱える。



ファーストクラスオブジェクトとは

・無名のリテラルとして表現可能
・変数に格納可能
・データ構造への組み込みが可能
・プロシージャや関数のパラメータとして渡すことができる
・プロシージャや関数の戻り値として返すことができる



def twice(f:(Int => Int))(x:Int):Int = f(f(x))




関数 twice は
Int 型の引数を受け取り Int 型の値を返す関数 f
を受け取り、
Int 型の引数を受け取り Int 型の値を返す関数
を返す関数



def add1(x:Int) = x + 1

> val add2 = twice(add1)(_)
add2: Int => Int = <function1>

> add2(3)
res1: Int = 5



Int 型の引数を受け取り
Int 型の値を返す関数
Int 型の引数を受け取り
> add2(3) Int 型の値を返す関数
res1: Int = 5





> add2(3) = twice(add1)(3) = add1(add1(3))
res1: Int = 5


処理の再利用の行いやすさ
パターンとしての高階関数



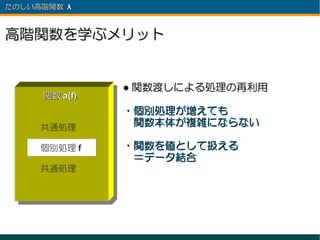
例えば、ある関数 a の大部分が
関数 a 共通処理で、一部が個別処理の場合

共通処理
例 ) ファイルの Open/Close
　　トランザクションの Begin/End
個別処理　　リトライ処理
　　 Tree の走査
共通処理



● 値渡しによる処理の分岐
関数 a(x)

共通処理・個別処理が増える度に、
　関数の処理が増大する
if(x == 1)
個別処理 1 ・関数の引数に制御情報を渡している
else 　＝制御結合
個別処理 2

共通処理



抽象クラス A
● 個別処理の抽象化
メソッド a （ template method パターン）
共通処理
・処理毎にクラスが増える
Call メソッド b

共通処理

抽象メソッド b



● 関数渡しによる処理の再利用
関数 a(f)
・個別処理が増えても
共通処理
　関数本体が複雑にならない

個別処理 f ・関数を値として扱える
　＝データ結合
共通処理



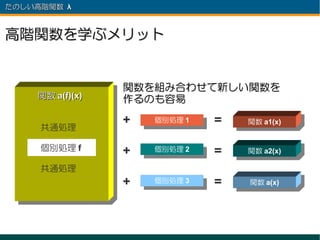
関数を組み合わせて新しい関数を
関数 a(f)(x) 作るのも容易

共通処理
+ 個別処理 11
個別処理 = 関数 a1(x)

個別処理 f + 個別処理 22
個別処理 = 関数 a2(x)

共通処理
+ 個別処理 33
個別処理 = 関数 a(x)

インターフェース渡し
があるじゃん！


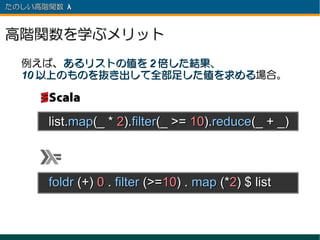
例えば、あるリストの値を 2 倍した結果、
10 以上のものを抜き出して全部足した値を求める場合。

list.map(_ * 2).filter(_ >= 10).reduce(_ + _)

foldr (+) 0 . filter (>=10) . map (*2) $ list



list.map(new Func1<Integer, Integer>() {
public Integer apply(Integer a) { return a * 2;}

}).filter(new Func1<Integer, Boolean>() {
public Boolean apply(Integer a) { return a >= 10;}

}).reduce(new Func2<Integer, Integer, Integer>() {
public Integer apply(Integer a, Integer b) { return a + b; }
});

やってられるか～！！



・高階関数は関数を引数に渡せるので、
　処理の再利用が行いやすい

・但し、型推論、ラムダ式など、手軽に関数を扱える
　言語サポートが備わっていることが重要


例えば、リストの全ての要素に関数を写す関数は map

List(1,2,3).map(_ * 2)

map (*2) [1,2,3]

JavaScript

[1,2,3].map(function(a) { return a * 2 })


例えば、 Scala の flatMap はモナドの bind と分かれば
以下の動作が容易に推測できる。

> List(1,2,3).flatMap(x => List(x*2))
res0: List[Int] = List(2, 4, 6)

> Some(1).flatMap(x => Some(x*2))
res1: Option[Int] = Some(2)



・関数型言語にはパターンがある。

・パターンを覚えれば、他の関数型言語でも応用が利く。


map 関数
map 関数
filter 関数
filter 関数

畳込み関数
畳込み関数

・神は言われた。「リストあれ」

・リストと関数型言語は関連が深い

・ Java やってて「あれ欲しい」は
　たいていリストの高階関数


リストのおさらい

0 :: 1 :: 2 :: 3 :: Nil

0 : 1 : 2 : 3 : []

[]

0 1 2 3

ヘッダテイルラスト Nil



つまりですね



こんなイメージ

ヘッダテイル
ラスト Nil


map 関数
map 関数
filter 関数
filter 関数

畳込み関数
畳込み関数



map 関数のイメージ

[1,2,3,4 ・・ ,n]
map f

[f(1), f(2), f(3), f(4) ・・ ,f(n)]

関数 f をリストに写す（ map over ）


こういう風に使います

let ベホマラー = map ベホイミ
let ルカナン = map ルカニ

let スクルト = map スカラ



map 関数の例

> map (x -> x * 2) [1,2,3]
[2,4,6]

> map (x -> "hoge" ++ show(x)) [1,2,3]
["hoge1","hoge2","hoge3"]



map 関数の実装

map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
ヘッダテイル



map 関数の実装

def map[B, That](f: A => B)
(implicit bf: CanBuildFrom[Repr, B, That])
: That = {
val b = bf(repr)
b.sizeHint(this)
for (x <- this) b += f(x)
b.result
}



map 関数の実装（簡略化）

def map[B, That](f: A => B)
def map[A, B](f: A => Bbf:List[B] = {
(implicit ): CanBuildFrom[Repr, B, That])
val b = new :ListBuffer[B]()
That = {
val b = bf(repr)
b.sizeHint(this)
b.sizeHint(this) buff += f(x)
for (x <- this)
for (x <- this) b += f(x)
b.result
}b.result
}



filter 関数のイメージ

[1,2,3,4 ・・ ,n]

filter (x => x < 4)

[1,2,3]

関数 f で要素を篩いに掛ける


こういう時に使います　ゲームしばり無視していますが。。

let レベル 5 デス = filter (not . is レベル 5)



filter 関数の例

> filter (x -> not(x `mod` 5 == 0)) [3,4,5,10,12]
[3,4,12]



filter 関数の実装

filter :: (a -> Bool) -> [a] -> [a]
filter _pred [] = []
filter pred (x:xs)
| pred x = x : filter pred xs
| otherwise = filter pred xs



filter 関数の実装

def filter(p: A => Boolean): Repr = {
val b = newBuilder
for (x <- this)
if (p(x)) b += x
b.result
}


foldl / foldr 関数のイメージ

foldl f 0 [1,2,3,4] foldr f 0 [1,2,3,4]
f f
f 4 1 f
f 3 2 f
f 2 3 f
0 1 4 0
関数 f でリストを畳み込んで単一の値を返す。
左からと右からの畳み込み関数がある。


一応やっときます


右も左もないですが

+ + + +

=



foldl / foldr 関数の例

> let add x y = x + y
> foldl add 0 [1,2,3,4]
10
> foldr add 0 [1,2,3,4]
10




> foldl add 0 [1,2,3,4]
= add(add(add(add(0, 1), 2), 3), 4)
= add(add(add(1, 2), 3), 4)
= add(add(3, 3), 4)
= add(6, 4)
=10

> foldr add 0 [1,2,3,4]
10




> foldl add 0 [1,2,3,4]
10
> foldr add 0 [1,2,3,4]
= add(1, add(2, add(3, add(4, 0))))
= add(1, add(2, add(3, 4)))
= add(1, add(2, 7))
= add(1, 9)
= 10



foldr 関数の実装

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr k z = go
where
go [] = z
go (y:ys) = y `k` go ys



foldr 関数の実装

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr k z = go
where
go [] = z
go (y:ys) = y `k` go ys

foldr k z [] = z
foldr k z (y:ys) = k y (foldr k z ys)



foldl 関数の実装

foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f z0 xs0 = lgo z0 xs0
where
lgo z [] = z
lgo z (x:xs) = lgo (f z x) xs



foldl 関数の実装

foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f z0 xs0 = lgo z0 xs0
where
lgo z [] = z
lgo z (x:xs) = lgo (f z x) xs

foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs



foldLeft 関数の実装 (Scala)

def foldLeft[B](z: B)(f: (B, A) => B): B = {
var acc = z
var these = this
while (!these.isEmpty) {
acc = f(acc, these.head)
these = these.tail
}
acc
}



foldRight 関数の実装 (Scala)

def foldRight[B](z: B)(f: (A, B) => B): B =
if (this.isEmpty) z
else f(head, tail.foldRight(z)(f))



Scala の foldRight 関数の注意点

scala> (1 to 10000).toList.foldLeft(0)(_ + _)
res0: Int = 50005000

scala> (1 to 10000).toList.foldRight(0)(_ + _)
java.lang.StackOverflowError



Range の場合は大丈夫

scala> (1 to 10000).foldLeft(0)(_ + _)
res0: Int = 50005000

scala> (1 to 10000).foldRight(0)(_ + _)
res1: Int = 50005000



Range の foldRight 関数の実装

def foldRight[B](z: B)(op: (A, B) => B): B =
reversed.foldLeft(z)((x, y) => op(y, x))

まさかの reversed ！

Reversed は List 型を返すので、
List の foldLeft が使われる


・高階関数は関数を引数に渡せるので、処理の再利用が
　行いやすい（型推論やラムダ式などの言語支援が重要）

・パターンを覚えると、他の関数型言語でも応用が利く

・リスト処理の高階関数のように、便利で強力な関数が
　最初から用意されている

ご清聴ありがとう
ございました！！

たのしい高階関数

More Related Content

たのしい高階関数