母平均の点推定では、標本平均のもつ「母平均がμ（ミュー）である集団から標本を抽出する場合、サンプルサイズ（＝標本の大きさ）が大きくなるにつれて、標本平均は母平均μに近づく」という性質を用いました（17-2章 大数の法則より）。このように推定できるのは、母平均の推定量が「一致性」と「不偏性」という2つの性質を満たすためです。

■一致性について

推定量を元に母平均や母分散のような分布のパラメータ（母数）を推測するとき、その推測が正確である必要があります。大数の法則は、サンプルサイズnが大きくなると、標本平均が母平均に近づくというものでした。このように、nが大きくなれば、推定量がだんだんと真のパラメータに近づく性質を「一致性」と言います。

推定量、真のパラメータをθと表記するとき、一致性を式で表すと次のようになります。

難しい式ですが、これを覚える必要はありません。この式は「nが大きくなれば、推定量は真のパラメータに近づく」ということ意味しています。

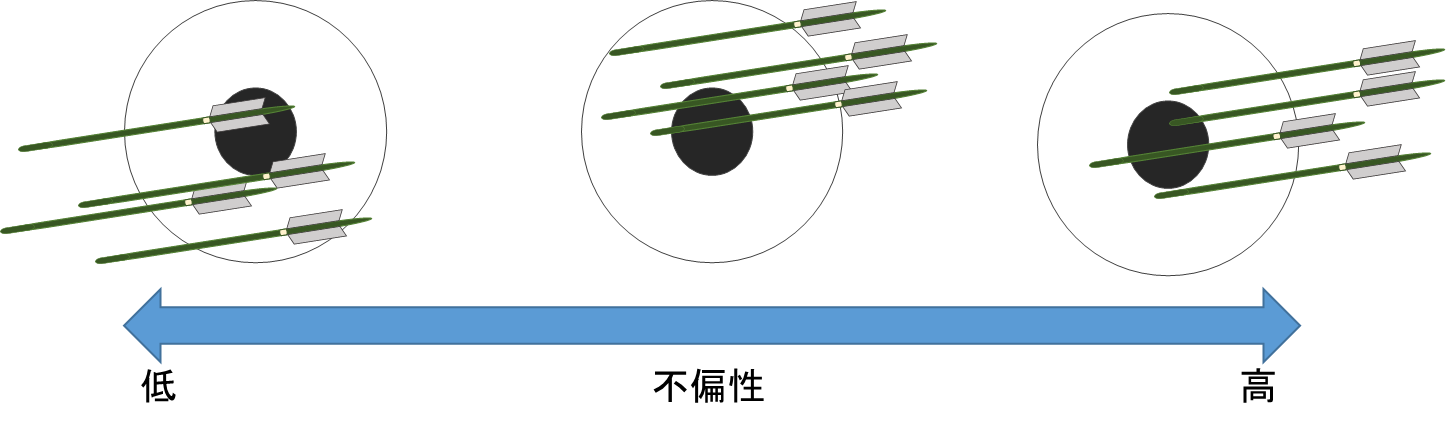
■不偏性について

推定量を元に母平均や母分散のような分布のパラメータ（母数）を推測するとき、その推測が真のパラメータから大きく外れてしまっては意味がありません。言い換えると、推定量の期待値がパラメータに一致する必要があります。この性質を「不偏性」と言います。不偏性を、推定量と真のパラメータを用いて表すと次のようになります。

これは、「nの値に関係なく、の期待値がであること」を示しています。つまり、nが小さい時にも大きい時にも、推定量の外れ具合が偏っていない（外れ具合が上にも下にも同じである）ことを表しています。

■標本平均の性質

標本平均は一致推定量であり不偏推定量です。そのため、標本平均の値を母平均の推定量として使うことができるわけです。