Двумерно пространство

Двумерна Декартова координатна система.

Двумерното пространство е геометричен модел, при който са нужни два параметъра за определяне на позицията на даден елемент (например точка). Редицата ℝ² от двойки реални числа с подходяща структура често служи като каноничен пример за двумерно Евклидово пространство.

Двумерното пространство може да се разглежда като проекция на физическата Вселена върху равнина. Обикновено тя се счита за Евклидово пространство, а двете измерения се наричат дължина и ширина.

Координатни системи

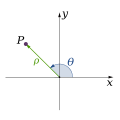
Аналитичната геометрия описва всяка точка в двумерно пространство чрез две координати. Две перпендикулярни координатни оси се пресичат една друга в началото на координатната система. Обикновено те се набелязват като x и y. Спрямо тези две оси позицията на всяка точка в двумерното пространство може да се представи като двойка реални числа, като всяко число е разстоянието на въпросната точка от началото на координатната система, измерено по оста. Друга широко използвана координатна система е полярната, която определя дадена точка по отношение на разстоянието ѝ от началото на координатната система и ъгъла ѝ спрямо отправен лъч.

• 
  Декартова координатна система
• 
  Полярна координатна система

В линейната алгебра

Друг математически начин за разглеждане на двумерното пространство се намира в линейната алгебра, където идеята за независимост е от ключово значение. Равнината има две измерения, тъй като дължината на правоъгълника е независима от ширината му. Технически, равнината е двумерна, тъй като всяка точка в нея може да бъде описана чрез линейна комбинация от два независими координатни вектора.

Скаларното произведение на двата вектора A = [A₁, A₂] и B = [B₁, B₂] е:

$\mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}$