Límit de Roche

Considerem un cos fluid que manté la seva estructura per la seva gravetat interna i que orbita al voltant d'un objecte major. En esta figura observem des de la part superior del pla orbital. Lluny del límit de Roche el fluid té una forma esfèrica.

Més a prop del límit de Roche el fluid és deformat per l'acció de forces de marea.

Dins del límit de Roche la gravetat del fluid no és prou per a mantindre la seva forma i el cos és trencat per l'acció de la força de marea.

Les fletxes roges representen la velocitat orbital de les restes disgregades del satèl·lit. Les partícules internes orbiten més de pressa que les exteriors.

La velocitat diferencial de rotació ocasiona finalment la formació d'un anell a partir del cos inicial.

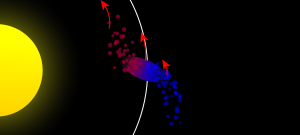
En astronomia, el límit de Roche és la distància a la qual un objecte que orbita un cos massiu mantenint la seua estructura únicament per la seva pròpia gravetat comença a desintegrar-se a causa de les forces de marea de l'objecte principal. Dins del límit de Roche, la força de la gravetat que el cos central exerceix sobre els extrems més pròxim i més allunyat del satèl·lit excedeix a la força de gravetat del satèl·lit. Aquest podrà ser destruït, per tant, per les forces de marea. El nom de límit de Roche prové de l'astrònom francés Édouard Roche, que primer va proposar aquest efecte i va calcular el límit teòric el 1848.

El límit de Roche depèn, per tant, de la gravetat del cos central, però també de les característiques de densitat del satèl·lit.

No s'ha de confondre amb el lòbul de Roche, un concepte teòric proposat també per Édouard Roche i que descriu el límit en què un objecte de poca massa en un sistema dominat per dos cossos majors és capturat per un d'aquests.

Alguns satèl·lits, tant naturals com artificials, orbiten a distàncies inferiors a la del límit de Roche, ja que mantenen el seua estructura per forces diferents de la gravetat (la resistència del material). Entre les llunes de Júpiter, tant Adrastea com Metis són exemples de cossos naturals que mantenen la seua cohesió més enllà dels seus límits de Roche. No obstant això, qualsevol objecte en la seva superfície pot ser desgranat per les forces de marea. Un cos amb menor cohesió, com un cometa, serà destruït en travessar el seu límit de Roche. El cometa Shoemaker-Levy 9 va travessar el límit de Roche de Júpiter al juliol de 1992 i es trencà en nombrosos fragments. El 1994, les restes del cometa van impactar sobre la superfície del planeta.

Atès que les forces de marea són superiors a la força de gravetat dins del límit de Roche, cap cos pot créixer per coalescència de partícules més xicotetes dins d'aquest límit. De fet, tots els anells planetaris es troben dins dels seus límits de Roche. Estos anells podrien ser les restes del disc d'acreció que no van arribar a la coalescència per a formar un satèl·lit, o podrien ser les restes d'un objecte que va travessar el límit de Roche i va ser destruït per les forces de marea.

El límit de Roche es defineix únicament en funció de les forces de gravetat, força de marea i autogravetat. En la pràctica, la qüestió de l'estabilitat estructural d'una lluna dependrà també de la seva velocitat de rotació i la força centrífuga provenint de la seva rotació.

Determinació del límit de Roche

Cossos rígids

El límit de Roche depèn de la rigidesa del satèl·lit orbitant el planeta. D'una banda, aquest podria ser una esfera perfecta i en est cas el límit de Roche és:

$d=R\left(2\;{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}\approx 1.260R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}$

en què $R$ és el radi del cos principal, $\rho _{M}$ és la seva densitat i $\rho _{m}$ és la densitat del satèl·lit.

Si la lluna té una densitat superior al doble de la del planeta, tal com pot ocórrer en un satèl·lit rocós orbitant un gegant gasós, llavors el límit de Roche estaria dins del mateix planeta i seria una magnitud no rellevant.

Cossos deformables

L'altre cas límit és un satèl·lit capaç de deformar-se sense oposar resistència, tal com faria un líquid. Encara que el càlcul exacte no pot realitzar-se analíticament, una aproximació prou bona pot donar-se per mitjà de la fórmula següent:

$d\approx 2.423R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}$

Derivació de la fórmula: Cossos rígids

Derivació de la fórmula del límit de Roche a partir d'una partícula test

Per a determinar el límit de Roche, considerarem una partícula de massa $u$ sobre la superfície d'un cos xicotet (satèl·lit) en les proximitats d'un cos de major massa (planeta). La nostra partícula $u$ experimentarà dues forces: la gravetat provinent del satèl·lit que la fa romandre sobre la seua superfície i la gravetat del planeta principal. Atès que el satèl·lit està en moviment orbital, la resultant de la gravetat exercida pel planeta és únicament la força de marea.

L'espenta de la gravetat $F_{G}$ sobre la partícula de massa $u$ sobre el satèl·lit de massa $m$ i radi $r$ pot expressar-se d'acord amb la llei de la gravitació universal de Newton:

$F_{G}={\frac {Gmu}{r^{2}}}$

La força de marea $F_{T}$ sobre la massa $u$ exercida pel planeta central de radi $R$ i a una distància $d$ entre els centres de massa d'ambdós cossos:

$F_{T}={\frac {2GMur}{d^{3}}}$

El límit de Roche s'aconsegueix quan l'espenta gravitacional i la força de marea es cancel·len l'una a l'altra:

$F_{G}=F_{T}$,

o bé,

${\frac {Gmu}{r^{2}}}={\frac {2GMur}{d^{3}}}$.

Expressió que ens permet calcular el límit de Roche, $d$:

$d=r\left(2M/m\right)^{\frac {1}{3}}$

No obstant això, és convenient expressar esta equació en una forma alternativa que no depenga del radi del satèl·lit, per la qual cosa reescriurem esta expressió en funció de les densitats del planeta i el satèl·lit.

La massa $M$ d'una esfera és de radi $R$ és:

$M={\frac {4\pi \rho _{M}R^{3}}{3}}$

I anàlogament per al segon cos:

$m={\frac {4\pi \rho _{m}r^{3}}{3}}$.

Substituint ambdues masses en l'equació del límit de Roche obtenim:

$d=r\left(2\rho _{M}R^{3}/\rho _{m}r^{3}\right)^{\frac {1}{3}}$

que pot simplificar-se en l'expressió habitual del límit de Roche.

$d=R\left(2\;{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}$

Derivació de la fórmula: cossos deformables no esfèrics

Una expressió una miqueta més precisa per al límit de Roche hauria de tenir en compte les deformacions produïdes en el satèl·lit per les forces de marea. En estos casos, el satèl·lit seria deformat en un esferoide el·líptic.

El càlcul exacte no pot realitzar-se analíticament. Històricament, Roche va derivar una aproximació numèrica per a est problema:

$d\approx 2.44R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}$

Amb l'ajuda d'ordinadors és senzill trobar una aproximació millor:

$d\approx 2.423R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}\left({\frac {(1+{\frac {m}{3M}})+{\frac {c}{3R}}(1+{\frac {m}{M}})}{1-{\frac {c}{R}}}}\right)^{\frac {1}{3}}$

en què $c/R$ és un factor que expressa el grau de deformació del cos principal.

El límit de Roche en exemples del sistema solar

La taula inferior mostra la densitat mitjana i el radi equatorial de diferents objectes del sistema solar:

Cos	Densitat (kg/m³)	Radi (m)
Sol	1,400	695,000,000
Júpiter	1,330	71,500,000
Terra	5,515	6,376,500
Lluna	3,340	1,737,400

Amb estes dades, el límit de Roche per a cossos rígids i cossos deformables pot ser fàcilment calculat. La densitat mitjana dels cometes pot considerar-se al voltant de 500 kg/m³. El vertader límit de Roche depèn de la flexibilitat del satèl·lit, per la qual cosa estarà en algun punt intermedi entre els límits calculats per al cos rígid i el cos perfectament deformable que hem calculat anteriorment. Si el cos central major té una densitat inferior a la meitat del cos orbitant, el límit de Roche s'aconseguix per davall del radi del planeta, per la qual cosa el satèl·lit no pot aconseguir tal límit. Aquest és el cas, per exemple, del límit de Roche per al sistema Sol-Terra. La taula següent dona els límits de Roche expressats en metres i en radis del cos central:

Cos	Satèl·lit	Límit de Roche (rígid)		Límit de Roche (no rígid)
		Distància (m)	Radi	Distància (m)	Radi
Terra	Lluna	9,495,665	1.49	18,261,459	2.86
Terra	Cometa	17,883,432	2.80	34,392,279	5.39
Sol	Terra	554,441,389	0.80	1,066,266,402	1.53
Sol	Cometa	1,234,186,562	1.78	2,373,509,071	3.42

És interessant considerar com de prop o lluny es troben les diferents llunes del sistema solar dels seus límits de Roche. La taula següent dona el radi orbital de cada satèl·lit dividit pels seus límits de Roche en els dos casos de cos rígid i flexible. En els casos dels planetes gegants, només s'han considerat els satèl·lits interiors més xicotets. Els satèl·lits principals com Io en Júpiter o Tità en Saturn es troben a distàncies molt superiors als seus límits de Roche.

Cos central	Satèl·lit	Radi orbital: límit de Roche
		(Rígid)	(No rígid)
Sol	Mercuri	104:1	54:1
Terra	Lluna	41:1	21:1
Mart	Fobos	171%	89%
	Deimos	456%	237%
Júpiter	Metis	191%	99%
	Adrastea	192%	100%
	Amaltea	178%	93%
	Tebé	331%	172%
Saturn	Pan	177%	92%
	Atles	182%	95%
	Prometeu	185%	96%
	Pandora	188%	98%
	Epimeteu	198%	103%
Urà	Cordèlia	155%	81%
	Ofèlia	168%	87%
	Bianca	184%	96%
	Cressida	193%	100%
Neptú	Nàiade	144%	75%
	Talassa	149%	78%
	Despina	157%	82%
	Galatea	184%	96%
	Larissa	219%	114%
Plutó	Caront	13:1	6.8:1

És interessant constatar com els satèl·lits menors dels planetes gegants es troben prop dels seus límits de Roche, i la seva estructura és mantinguda per forces internes de cohesió i no únicament per la seva gravetat. En la regió dominada per anells com els anells de Saturn, és impossible l'agrupació de les partícules en cossos majors perquè serien disgregats pels efectes de la força de marea. Estos satèl·lits van tenir probablement el seu origen en regions més allunyades dels planetes gegants i les seves òrbites van ser modificades posteriorment, potser per la interacció gravitatòria dels altres satèl·lits. Alternativament, potser van ser formats en regions pròximes a les seves posicions actuals, quan els planetes centrals encara estaven en plena formació i tenien una massa inferior. Aquest segon escenari resulta, això no obstant, menys probable.

Referències

• Édouard Roche: La figure d'une masse fluide soumise à l'attraction d'un point éloigné, Acad. des sciences de Montpeller, Vol. 1 (1847-50) p. 243.

Vegeu també

• Lòbul de Roche
• Força de marea
• Esfera de Hill