Bohemian matrices: Difference between revisions
Undid revision 1231125752 by Cdkw2 (talk) I'm sorry, but if you wish to contribute to this article then you must learn to do so without removing every citation in the process. I will provide resources on your talk page |
Citation bot (talk | contribs) Alter: title, template type. Add: website, chapter-url, chapter, authors 1-1. Removed or converted URL. Removed parameters. Some additions/deletions were parameter name changes. | Use this bot. Report bugs. | Suggested by Headbomb | Linked from Wikipedia:WikiProject_Academic_Journals/Journals_cited_by_Wikipedia/Sandbox | #UCB_webform_linked 90/748 |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Set of matrices}} |
{{Short description|Set of matrices}} |
||
{{tone|date=March 2022}} |
|||
A '''Bohemian matrix family'''<ref>{{cite news|last1=Higham|first1=Nicholas J|date=December 2018|title=Rhapsodizing about Bohemian Matrices|publisher=Society for Industrial and Applied Mathematics|url=https://sinews.siam.org/Details-Page/rhapsodizing-about-bohemian-matrices|url-status=live|access-date=1 March 2022|archive-url=https://web.archive.org/web/20220228020232/https://sinews.siam.org/Details-Page/rhapsodizing-about-bohemian-matrices|archive-date=28 February 2022}}</ref> is a set of |
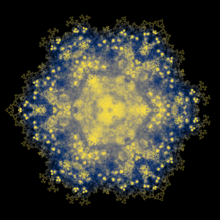
A '''Bohemian matrix family'''<ref>{{cite news|last1=Higham|first1=Nicholas J|date=December 2018|title=Rhapsodizing about Bohemian Matrices|publisher=Society for Industrial and Applied Mathematics|url=https://sinews.siam.org/Details-Page/rhapsodizing-about-bohemian-matrices|url-status=live|access-date=1 March 2022|archive-url=https://web.archive.org/web/20220228020232/https://sinews.siam.org/Details-Page/rhapsodizing-about-bohemian-matrices|archive-date=28 February 2022}}</ref> is a set of [[Matrix (mathematics)|matrices]] whose entries are members of a fixed, finite, and discrete set, referred to as the "population". The term "Bohemian" was first used to refer to matrices with entries consisting of integers of bounded height, hence the name, derived from the acronym '''BO'''unded '''HE'''ight '''M'''atrix of '''I'''ntegers (BOHEMI).<ref>{{Cite book |last1=Corless |first1=Robert |last2=Labahn |first2=George |last3=Piponi |first3=Dan |last4=Rafiee Sevyeri |first4=Leili |chapter=Bohemian Matrix Geometry |date=2022-07-05 |title=Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation |chapter-url=https://doi.org/10.1145/3476446.3536177 |series=ISSAC '22 |location=New York, NY, USA |publisher=Association for Computing Machinery |pages=361–370 |doi=10.1145/3476446.3536177 |isbn=978-1-4503-8688-3|arxiv=2202.07769 }}</ref> The majority of published research on these matrix families studies populations of integers, although this is not strictly true of all possible Bohemian matrices. There is no single family of Bohemian matrices. Instead, a matrix can be said to be Bohemian with respect to a set from which its entries are drawn. Bohemian matrices may possess additional structure. For example, they may be [[Toeplitz matrices]] or [[upper Hessenberg matrix|upper Hessenberg matrices]].[[File:Exhaustivepop CubeRootsOfMinusOne cividis 15N4782969.png|thumb|alt=Blue, yellow, and gold fractal doily with a tilted hamster-face in the middle (that's just pareidolia, but inescapable). Triple symmetry with sharp points at 9 o'clock, at 1 o'clock, and 5 o'clock. |A density plot of all eigenvalues of all dimensions in 15x15 Bohemian upper Hessenberg zero diagonal matrices with population cube roots of -1]] |
||
==Applications== |
==Applications== |
||
===Software testing=== |
===Software testing=== |
||
Bohemian matrices are used in software testing, particularly in [[linear algebra]] applications. They are often distinctly represented on computers<ref name="higham2">{{cite web|last1=Higham|first1=Nicholas J|title=Bohemian Matrices in Numerical Linear Algebra|url=https://www.maths.manchester.ac.uk/~higham/conferences/bohemian/higham_bohemian18.pdf|url-status=dead|archive-url=https://web.archive.org/web/20201113070852/https://www.maths.manchester.ac.uk/~higham/conferences/bohemian/higham_bohemian18.pdf|archive-date=13 November 2020|access-date=2 March 2022|website=Nick Higham—Conferences}}</ref> and are identifiable for extreme behavior through exhaustive search (for small dimensions), random sampling, or optimization techniques. Steven E. Thornton utilized these concepts to develop a tool that solved over two [[trillion]] eigenvalue problems, revealing instances of convergence failure in some popular software systems.<ref>{{cite thesis|last1=Thornton|first1=Steven E|title=Algorithms for Bohemian Matrices|type=PhD thesis|publisher=Western University|date=April 2019|url=https://ir.lib.uwo.ca/etd/6069/|access-date=1 March 2022|archive-date=7 March 2022|archive-url=https://web.archive.org/web/20220307103416/https://ir.lib.uwo.ca/etd/6069/|url-status=live}}</ref> |
|||
The anymatrix toolbox is an extensible [[MATLAB]] [[Matrix (mathematics)|matrix]] tool that provides a set of sorted Bohemian matrices and utilities for property-based queries of the set.<ref>{{cite web |url=https://github.com/mmikaitis/anymatrix |title=anymatrix |last1=Mikaitis |first1=Mantas |last2=Higham |first2=Nicholas J. |website=[[GitHub]] |date=31 March 2021 |accessdate=29 June 2024 }}</ref> |
|||
Steven E. Thornton used this concept to develop a tool that solved over two [[trillion]] eigenvalue problems. In doing so, he uncovered instances of convergence failure in some popular software systems.<ref>{{cite thesis|last1=Thornton|first1=Steven E|title=Algorithms for Bohemian Matrices|type=PhD thesis|publisher=Western University|date=April 2019|url=https://ir.lib.uwo.ca/etd/6069/|access-date=1 March 2022|archive-date=7 March 2022|archive-url=https://web.archive.org/web/20220307103416/https://ir.lib.uwo.ca/etd/6069/|url-status=live}}</ref> |
|||
An ''anymatrix'' is an extensible [[MATLAB]] [[Matrix (mathematics)|matrix]] collection capturing a set of optimal classes of Bohemian matrices. |
|||
===Improved bounds=== |
===Improved bounds=== |
||
In a |
In a presentation at the 2018 Bohemian Matrices and Applications Workshop, [[Nick Higham (mathematician)|Nick Higham]] (co-author of the anymatrix toolbox) discussed how he used [[genetic algorithms]] on Bohemian matrices with population {{math|1=''P''={{mset|-1, 0, 1}}}} to refine lower bounds on the maximal growth factor for [[Pivot element#Partial, rook, and complete pivoting|rook pivoting]].<ref name="higham">{{cite web|last1=Higham|first1=Nicholas J|title=Bohemian Matrices in Numerical Linear Algebra|url=https://www.maths.manchester.ac.uk/~higham/conferences/bohemian/higham_bohemian18.pdf|url-status=dead|archive-url=https://web.archive.org/web/20201113070852/https://www.maths.manchester.ac.uk/~higham/conferences/bohemian/higham_bohemian18.pdf|archive-date=13 November 2020|access-date=2 March 2022|website=Nick Higham—Conferences}}</ref> |
||
==Connections to other fields== |
==Connections to other fields== |
||
===Random matrices=== |
===Random matrices=== |
||
Bohemian matrices can be studied through random sampling |
Bohemian matrices can be studied through random sampling, a process that intersects with the field of random matrices. However, the study of random matrices has predominantly focused on real symmetric or [[Hermitian matrices]], or matrices with entries drawn from a continuous distribution, such as [[Gaussian ensemble]]s. Notable exceptions to this focus include the work of [[Terence Tao]] and [[Van Vu]].<ref name=bernoulli>{{cite journal|last1=Tao|first1=Terence|last2=Vu|first2=Van|title=On random ±1 matrices: Singularity and determinant|journal=Random Structures and Algorithms|date=January 2006|volume=28|issue=1|pages=1–23|doi=10.1002/rsa.20109|s2cid=5361802|url=https://doi.org/10.1002/rsa.20109|access-date=2 March 2022|arxiv=math/0411095}}</ref><ref>{{cite book|last1=Vu|first1=Van|title=Horizons of Combinatorics|chapter=Random Discrete Matrices|series=Bolyai Society Mathematical Studies|date=2008|volume=17|pages=257–289|doi=10.1007/978-3-540-77200-2_13|arxiv=math/0611321|isbn=978-3-540-77199-9|s2cid=118703720 }}</ref> |
||
===Bernoulli and Hadamard matrices=== |
===Bernoulli and Hadamard matrices=== |
||
The term ''Bernoulli matrices'' is sometimes used to describe matrices with entries constrained to {{math|±1}},<ref name="bernoulli2">{{cite journal|last1=Tao|first1=Terence|last2=Vu|first2=Van|date=January 2006|title=On random ±1 matrices: Singularity and determinant|url=https://doi.org/10.1002/rsa.20109|journal=Random Structures and Algorithms|volume=28|issue=1|pages=1–23|doi=10.1002/rsa.20109|s2cid=5361802|access-date=2 March 2022|arxiv=math/0411095}}</ref> classifying them as Bohemian matrices. A [[Hadamard matrix]] is a Bernoulli matrix that satisfies an additional property, namely that its [[determinant]] is maximal. Hadamard matrices (and Bernoulli matrices) have been studied for far longer than the term "Bohemian matrix" has existed. The questions posed about Hadamard matrices, such as those concerning maximal determinants, can also be applied to other Bohemian matrices. One generalization of Hadamard matrices includes [[Butson-type Hadamard matrices]], whose entries are {{math|''q''}}th [[Root of unity|roots of unity]] for {{math|''q'' > 2}}, and can also be considered prototypical Bohemian matrices. |
|||
===Graph theory=== |
===Graph theory=== |
||
Matrices with discrete entries, particularly [[Logical matrix|incidence matrices]], play a crucial role in understanding graph theory. The |
Matrices with discrete entries, particularly [[Logical matrix|incidence matrices]], play a crucial role in understanding graph theory. The results from graph theory research can elucidate phenomena observed in Bohemian matrix experiments. Conversely, experiments conducted using Bohemian matrices can provide valuable insights into graph-related problems.<ref name=small01>{{cite journal|last1=Živković|first1=Miodrag|title=Classification of small (0, 1) matrices|journal=Linear Algebra and Its Applications|date=2006|volume=414|issue=1|pages=310–346|doi=10.1016/j.laa.2005.10.010|doi-access=free|arxiv=math/0511636}}</ref> |
||
===Combinatorics=== |
===Combinatorics=== |
||
Several open problems listed in the [[Encyclopedia of Integer Sequences]] concerning Bohemian matrices are [[Combinatorics|combinatoric]] in nature. For instance, A306782 lists a table of the number of distinct minimal polynomials for Bernoulli matrices (Bohemian matrices with entries {{math|±1}}) up to dimension 5. The numbers for higher dimensions remain unknown. The number of valid Bernoulli matrices of dimension 6 is {{math|1= 2<sup>36</sup>=68,719,476,736}}; while this set could be exhaustively searched (it is [[delightfully parallel]]), the greater-than-exponential growth of the number of matrices quickly grows beyond the limits of numerical analysis. There are symmetries that might be taken advantage of, as is done<ref name=small01/> for zero-one matrices, but these require sophisticated combinatorics knowledge. |
|||
===Number theory=== |
===Number theory=== |
||
Many number theorists have studied [[polynomials]] with restricted coefficients. For instance, [[Littlewood polynomial]]s have coefficients {{math| ±1}} in the monomial basis. Researchers such as [[Kurt Mahler]],<ref>{{cite journal|last1=Mahler|first1=Kurt|title=On two extremum properties of polynomials|journal=Illinois Journal of Mathematics|date=1963|volume=7|issue=4|pages=681–701|doi=10.1215/ijm/1255645104|s2cid=118793107|doi-access=free}}</ref> [[Andrew Odlyzko]], [[Bjorn Poonen]]<ref>{{cite journal|last1=Odlyzko|first1=Andrew|title=Zeros of polynomials with 0,1 coefficients|journal=Algorithms Seminar|date=September 1992|page=169|citeseerx=10.1.1.47.9327}}</ref> and [[Peter Borwein]] have contributed to this field. By using [[companion matrices]], these polynomial problems with restricted coefficients can be framed as Bohemian matrix problems. However, the [[characteristic polynomial]] of a Bohemian matrix may have coefficients that are exponentially large in the matrix dimension, so the reverse transformation is not always applicable.<ref>{{cite journal|last1=Borwein|first1=Peter B.|last2=Jörgenson|first2=Loki|title=Visible Structures in Number Theory|journal=American Mathematical Monthly|date=December 2001|volume=108|issue=10|pages=897–910|doi=10.1080/00029890.2001.11919824|jstor=2695413|s2cid=454318|url=https://www.jstor.org/stable/2695413|access-date=3 March 2022}}</ref><ref>{{cite journal|last1=Calkin|first1=Neil J|last2=Chan|first2=Eunice Y.S.|last3=Corless|first3=Robert M.|title=Some facts and conjectures about Mandelbrot polynomials|journal=Maple Transactions|date=2 June 2021|volume=1|issue=1|page=13|doi=10.5206/mt.v1i1.14037|s2cid=242158547|author1-link=Neil J. Calkin|doi-access=free}}</ref> |
|||
By using [[companion matrices]], each of these restricted-coefficient polynomial problems can be considered to be a Bohemian matrix problem. However, the [[characteristic polynomial]] of a Bohemian matrix might have coefficients that are exponentially large in the dimension, so the converse is not true and these areas of study are not equivalent.<ref>{{cite journal|last1=Calkin|first1=Neil J|last2=Chan|first2=Eunice Y.S.|last3=Corless|first3=Robert M.|title=Some facts and conjectures about Mandelbrot polynomials|journal=Maple Transactions|date=2 June 2021|volume=1|issue=1|page=13|doi=10.5206/mt.v1i1.14037|s2cid=242158547|author1-link=Neil J. Calkin|doi-access=free}}</ref> |
|||
Connections to [[Magic Squares]] are explored in [[Kathleen Ollerenshaw]]'s book with D. Brée.<ref>{{cite book|last1=Ollerenshaw|first1=Kathleen|last2=Brée|first2=D|title=Most-perfect pandiagonal magic squares|date=1998|publisher=IMA}}</ref> |
Connections to [[Magic Squares]] are explored in [[Kathleen Ollerenshaw]]'s book with D. Brée.<ref>{{cite book|last1=Ollerenshaw|first1=Kathleen|last2=Brée|first2=D|title=Most-perfect pandiagonal magic squares|date=1998|publisher=IMA}}</ref> Furthermore, Bohemian matrices are explicitly connected to [[quadratic forms]] in certain papers.<ref>{{cite journal|last1=Higham|first1=Nicholas J|last2=Lettington|first2=Matthew|title=Optimizing and Factorizing the Wilson Matrix|journal=The American Mathematical Monthly|date=2022|volume=129|issue=5|pages=454–465|url=http://eprints.maths.manchester.ac.uk/2803/|access-date=3 March 2022|doi=10.1080/00029890.2022.2038006|s2cid=233322415|archive-date=3 March 2022|archive-url=https://web.archive.org/web/20220303183937/http://eprints.maths.manchester.ac.uk/2803/|url-status=live}}</ref> |
||
===Solution of polynomial equations=== |
===Solution of polynomial equations=== |
||
To find the [[Zero of a function|roots]] of a polynomial, one can construct a [[companion matrix]] |
To find the [[Zero of a function|roots]] of a polynomial, one can construct a corresponding [[companion matrix]] and solve for its eigenvalues. These eigenvalues correspond to the roots of the original polynomial. This method is commonly used in [https://numpy.org/doc/stable/reference/routines.polynomials.html NumPy's polynomial package] and is generally numerically stable,<ref>{{cite journal|last1=Edelman|first1=Alan|last2=Murakami|first2=H|title=Polynomial roots from companion matrix eigenvalues|journal=Mathematics of Computation|date=April 1995|volume=64|issue=210|pages=763–776|doi=10.1090/S0025-5718-1995-1262279-2|bibcode=1995MaCom..64..763E|url=https://www.ams.org/journals/mcom/1995-64-210/S0025-5718-1995-1262279-2/S0025-5718-1995-1262279-2.pdf|access-date=2 March 2022|archive-date=24 January 2022|archive-url=https://web.archive.org/web/20220124024358/https://www.ams.org/journals/mcom/1995-64-210/S0025-5718-1995-1262279-2/S0025-5718-1995-1262279-2.pdf|url-status=live}}</ref> though it may occasionally struggle with polynomials that have large coefficients or are [[ill-conditioned]]. |
||
Improving this situation involves finding a minimal height companion matrix for the polynomial within a Bohemian matrix family.<ref>{{cite journal|last1=Chan|first1=Eunice Y.S.|last2=Corless|first2=Robert M.|title=A new kind of companion matrix|journal=Electronic Journal of Linear Algebra|date=6 February 2017|volume=32|pages=335–342|doi=10.13001/1081-3810.3400|doi-access=free}}</ref> However, no efficient general-purpose techniques are currently known for this approach. |
|||
==History== |
==History== |
||
The |
The term "Bohemian matrices" and the concept of categorizing problems in this manner first appeared in a publication by [[ISSAC]] in 2016.<ref |
||
name=thornton>{{cite journal|last1=Corless|first1=Robert M.|last2=Thornton|first2=Steven E.|title=The Bohemian Eigenvalue Project|journal=ACM Communications in Computer Algebra|date=2017|volume=50|issue=4|pages=158–160|doi=10.1145/3055282.3055289|s2cid=34583673|url=https://dl.acm.org/doi/abs/10.1145/3055282.3055289|access-date=28 February 2022|archive-date=1 March 2022|archive-url=https://web.archive.org/web/20220301172005/https://dl.acm.org/doi/abs/10.1145/3055282.3055289|url-status=live}}</ref> The name |
name=thornton>{{cite journal|last1=Corless|first1=Robert M.|last2=Thornton|first2=Steven E.|title=The Bohemian Eigenvalue Project|journal=ACM Communications in Computer Algebra|date=2017|volume=50|issue=4|pages=158–160|doi=10.1145/3055282.3055289|s2cid=34583673|url=https://dl.acm.org/doi/abs/10.1145/3055282.3055289|access-date=28 February 2022|archive-date=1 March 2022|archive-url=https://web.archive.org/web/20220301172005/https://dl.acm.org/doi/abs/10.1145/3055282.3055289|url-status=live}}</ref> The name originated from the mnemonic BOunded HEight Matrix of Integers (BOHEMI), although the classification has since been expanded to include other discrete populations,<ref>{{cite journal|last1=Corless|first1=Robert|title=What can we learn from Bohemian Matrices|journal=Maple Transactions|date=2 June 2021|volume=1|issue=1|doi=10.5206/mt.v1i1.14039|s2cid=241595165|doi-access=free}}</ref> such as [[Gaussian integers]]. The utility and scope of this categorization are becoming increasingly recognized, with the first significant journal publication<ref>{{cite journal|last1=Chan|first1=Eunice Y.S.|last2=Corless|first2=Robert M.|last3=Gonzalez-Vega|first3=Laureano|last4=Sendra|first4=J. Rafael|last5=Sendra|first5=Juana|last6=Thornton|first6=Steven E.|title=Upper Hessenberg and Toeplitz Bohemians|journal=Linear Algebra and Its Applications|date=September 2020|volume=601|pages=72–100|doi=10.1016/j.laa.2020.03.037|arxiv=1907.10677|s2cid=198899515|url=https://doi.org/10.1016/j.laa.2020.03.037|access-date=3 March 2022|archive-date=13 August 2023|archive-url=https://web.archive.org/web/20230813130658/https://www.sciencedirect.com/science/article/abs/pii/S0024379520301713?via%3Dihub|url-status=live}}</ref> following smaller earlier publications. As of March 2022, several publications explicitly use the term "Bohemian matrices," in addition to those already cited in this article.<ref>{{cite journal|last1=Fasi|first1=Massimiliano|last2=Negri Porzio|first2=Gian Maria|title=Determinants of normalized Bohemian upper Hessenberg matrices|journal=The Electronic Journal of Linear Algebra|date=2020|volume=36|issue=36|pages=352–366|doi=10.13001/ela.2020.5053|s2cid=191136476|doi-access=free}}</ref><ref>{{cite journal|last1=Chan|first1=Eunice Y.S.|last2=Corless|first2=Robert M.|last3=Gonzalez-Vega|first3=Laureano|last4=Sendra|first4=J. Rafael|last5=Sendra|first5=Juana|title=Inner Bohemian Inverses|journal=Applied Mathematics and Computation|date=May 2022|volume=421|issue=15|page=126945|doi=10.1016/j.amc.2022.126945|s2cid=246318540|doi-access=free}}</ref><ref>{{cite journal|last1=Bogoya|first1=Manuel|last2=Serra-Capizzano|first2=Stefano|last3=Trotti|first3=Ken|title=Upper Hessenberg and Toeplitz Bohemian matrix sequences: a note on their asymptotical eigenvalues and singular values|journal=Electronic Transactions on Numerical Analysis|date=2022|volume=55|pages=76–91|doi=10.1553/etna_vol55s76|s2cid=243772914|url=https://etna.math.kent.edu/vol.55.2022/pp76-91.dir/pp76-91.pdf|access-date=3 March 2022|archive-date=3 March 2022|archive-url=https://web.archive.org/web/20220303160804/https://etna.math.kent.edu/vol.55.2022/pp76-91.dir/pp76-91.pdf|url-status=live}}</ref> |
||
The |
The inaugural workshop on Bohemian matrices was held in 2018 at the [[University of Manchester]], titled "Bohemian Matrices and Applications." The concept is akin to the specialization suggested by [[George Pólya]], titled "Bohemian Matrices and Applications." The concept is akin to the specialization suggested by [[Littlewood polynomial]]. |
||
This concept shares similarities with '''sign pattern matrices''', where two matrices with real entries are deemed equivalent if corresponding entries have the same sign.<ref>{{cite book|last1=Hall|first1=Frank J|title=Sign Pattern Matrices|last2=Li|first2=Zhongshan|date=2013|publisher=CRC Press|editor1-last=Hogben|editor1-first=Leslie|edition=2nd|location=Handbook of Linear Algebra|pages=42-1—42-32}}</ref> A Bohemian matrix with the population {{math|1=''P''={{mset|-1, 0, 1}}}} is an example of a sign pattern matrix and adheres to the defined properties but may also exhibit unique characteristics specific to its Bohemian nature. |
|||
==References== |
==References== |
||
Latest revision as of 04:03, 12 August 2024
A Bohemian matrix family[1] is a set of matrices whose entries are members of a fixed, finite, and discrete set, referred to as the "population". The term "Bohemian" was first used to refer to matrices with entries consisting of integers of bounded height, hence the name, derived from the acronym BOunded HEight Matrix of Integers (BOHEMI).[2] The majority of published research on these matrix families studies populations of integers, although this is not strictly true of all possible Bohemian matrices. There is no single family of Bohemian matrices. Instead, a matrix can be said to be Bohemian with respect to a set from which its entries are drawn. Bohemian matrices may possess additional structure. For example, they may be Toeplitz matrices or upper Hessenberg matrices.
Applications
[edit]Software testing
[edit]Bohemian matrices are used in software testing, particularly in linear algebra applications. They are often distinctly represented on computers[3] and are identifiable for extreme behavior through exhaustive search (for small dimensions), random sampling, or optimization techniques. Steven E. Thornton utilized these concepts to develop a tool that solved over two trillion eigenvalue problems, revealing instances of convergence failure in some popular software systems.[4]
The anymatrix toolbox is an extensible MATLAB matrix tool that provides a set of sorted Bohemian matrices and utilities for property-based queries of the set.[5]
Improved bounds
[edit]In a presentation at the 2018 Bohemian Matrices and Applications Workshop, Nick Higham (co-author of the anymatrix toolbox) discussed how he used genetic algorithms on Bohemian matrices with population P={-1, 0, 1} to refine lower bounds on the maximal growth factor for rook pivoting.[6]
Connections to other fields
[edit]Random matrices
[edit]Bohemian matrices can be studied through random sampling, a process that intersects with the field of random matrices. However, the study of random matrices has predominantly focused on real symmetric or Hermitian matrices, or matrices with entries drawn from a continuous distribution, such as Gaussian ensembles. Notable exceptions to this focus include the work of Terence Tao and Van Vu.[7][8]
Bernoulli and Hadamard matrices
[edit]The term Bernoulli matrices is sometimes used to describe matrices with entries constrained to ±1,[9] classifying them as Bohemian matrices. A Hadamard matrix is a Bernoulli matrix that satisfies an additional property, namely that its determinant is maximal. Hadamard matrices (and Bernoulli matrices) have been studied for far longer than the term "Bohemian matrix" has existed. The questions posed about Hadamard matrices, such as those concerning maximal determinants, can also be applied to other Bohemian matrices. One generalization of Hadamard matrices includes Butson-type Hadamard matrices, whose entries are qth roots of unity for q > 2, and can also be considered prototypical Bohemian matrices.
Graph theory
[edit]Matrices with discrete entries, particularly incidence matrices, play a crucial role in understanding graph theory. The results from graph theory research can elucidate phenomena observed in Bohemian matrix experiments. Conversely, experiments conducted using Bohemian matrices can provide valuable insights into graph-related problems.[10]
Combinatorics
[edit]Several open problems listed in the Encyclopedia of Integer Sequences concerning Bohemian matrices are combinatoric in nature. For instance, A306782 lists a table of the number of distinct minimal polynomials for Bernoulli matrices (Bohemian matrices with entries ±1) up to dimension 5. The numbers for higher dimensions remain unknown. The number of valid Bernoulli matrices of dimension 6 is 236=68,719,476,736; while this set could be exhaustively searched (it is delightfully parallel), the greater-than-exponential growth of the number of matrices quickly grows beyond the limits of numerical analysis. There are symmetries that might be taken advantage of, as is done[10] for zero-one matrices, but these require sophisticated combinatorics knowledge.
Number theory
[edit]Many number theorists have studied polynomials with restricted coefficients. For instance, Littlewood polynomials have coefficients ±1 in the monomial basis. Researchers such as Kurt Mahler,[11] Andrew Odlyzko, Bjorn Poonen[12] and Peter Borwein have contributed to this field. By using companion matrices, these polynomial problems with restricted coefficients can be framed as Bohemian matrix problems. However, the characteristic polynomial of a Bohemian matrix may have coefficients that are exponentially large in the matrix dimension, so the reverse transformation is not always applicable.[13][14]
Connections to Magic Squares are explored in Kathleen Ollerenshaw's book with D. Brée.[15] Furthermore, Bohemian matrices are explicitly connected to quadratic forms in certain papers.[16]
Solution of polynomial equations
[edit]To find the roots of a polynomial, one can construct a corresponding companion matrix and solve for its eigenvalues. These eigenvalues correspond to the roots of the original polynomial. This method is commonly used in NumPy's polynomial package and is generally numerically stable,[17] though it may occasionally struggle with polynomials that have large coefficients or are ill-conditioned.
Improving this situation involves finding a minimal height companion matrix for the polynomial within a Bohemian matrix family.[18] However, no efficient general-purpose techniques are currently known for this approach.
History
[edit]The term "Bohemian matrices" and the concept of categorizing problems in this manner first appeared in a publication by ISSAC in 2016.[19] The name originated from the mnemonic BOunded HEight Matrix of Integers (BOHEMI), although the classification has since been expanded to include other discrete populations,[20] such as Gaussian integers. The utility and scope of this categorization are becoming increasingly recognized, with the first significant journal publication[21] following smaller earlier publications. As of March 2022, several publications explicitly use the term "Bohemian matrices," in addition to those already cited in this article.[22][23][24]
The inaugural workshop on Bohemian matrices was held in 2018 at the University of Manchester, titled "Bohemian Matrices and Applications." The concept is akin to the specialization suggested by George Pólya, titled "Bohemian Matrices and Applications." The concept is akin to the specialization suggested by Littlewood polynomial.
This concept shares similarities with sign pattern matrices, where two matrices with real entries are deemed equivalent if corresponding entries have the same sign.[25] A Bohemian matrix with the population P={-1, 0, 1} is an example of a sign pattern matrix and adheres to the defined properties but may also exhibit unique characteristics specific to its Bohemian nature.
References
[edit]- ^ Higham, Nicholas J (December 2018). "Rhapsodizing about Bohemian Matrices". Society for Industrial and Applied Mathematics. Archived from the original on 28 February 2022. Retrieved 1 March 2022.
- ^ Corless, Robert; Labahn, George; Piponi, Dan; Rafiee Sevyeri, Leili (2022-07-05). "Bohemian Matrix Geometry". Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation. ISSAC '22. New York, NY, USA: Association for Computing Machinery. pp. 361–370. arXiv:2202.07769. doi:10.1145/3476446.3536177. ISBN 978-1-4503-8688-3.
- ^ Higham, Nicholas J. "Bohemian Matrices in Numerical Linear Algebra" (PDF). Nick Higham—Conferences. Archived from the original (PDF) on 13 November 2020. Retrieved 2 March 2022.
- ^ Thornton, Steven E (April 2019). Algorithms for Bohemian Matrices (PhD thesis). Western University. Archived from the original on 7 March 2022. Retrieved 1 March 2022.
- ^ Mikaitis, Mantas; Higham, Nicholas J. (31 March 2021). "anymatrix". GitHub. Retrieved 29 June 2024.
- ^ Higham, Nicholas J. "Bohemian Matrices in Numerical Linear Algebra" (PDF). Nick Higham—Conferences. Archived from the original (PDF) on 13 November 2020. Retrieved 2 March 2022.
- ^ Tao, Terence; Vu, Van (January 2006). "On random ±1 matrices: Singularity and determinant". Random Structures and Algorithms. 28 (1): 1–23. arXiv:math/0411095. doi:10.1002/rsa.20109. S2CID 5361802. Retrieved 2 March 2022.
- ^ Vu, Van (2008). "Random Discrete Matrices". Horizons of Combinatorics. Bolyai Society Mathematical Studies. Vol. 17. pp. 257–289. arXiv:math/0611321. doi:10.1007/978-3-540-77200-2_13. ISBN 978-3-540-77199-9. S2CID 118703720.
- ^ Tao, Terence; Vu, Van (January 2006). "On random ±1 matrices: Singularity and determinant". Random Structures and Algorithms. 28 (1): 1–23. arXiv:math/0411095. doi:10.1002/rsa.20109. S2CID 5361802. Retrieved 2 March 2022.
- ^ a b Živković, Miodrag (2006). "Classification of small (0, 1) matrices". Linear Algebra and Its Applications. 414 (1): 310–346. arXiv:math/0511636. doi:10.1016/j.laa.2005.10.010.
- ^ Mahler, Kurt (1963). "On two extremum properties of polynomials". Illinois Journal of Mathematics. 7 (4): 681–701. doi:10.1215/ijm/1255645104. S2CID 118793107.
- ^ Odlyzko, Andrew (September 1992). "Zeros of polynomials with 0,1 coefficients". Algorithms Seminar: 169. CiteSeerX 10.1.1.47.9327.
- ^ Borwein, Peter B.; Jörgenson, Loki (December 2001). "Visible Structures in Number Theory". American Mathematical Monthly. 108 (10): 897–910. doi:10.1080/00029890.2001.11919824. JSTOR 2695413. S2CID 454318. Retrieved 3 March 2022.
- ^ Calkin, Neil J; Chan, Eunice Y.S.; Corless, Robert M. (2 June 2021). "Some facts and conjectures about Mandelbrot polynomials". Maple Transactions. 1 (1): 13. doi:10.5206/mt.v1i1.14037. S2CID 242158547.
- ^ Ollerenshaw, Kathleen; Brée, D (1998). Most-perfect pandiagonal magic squares. IMA.
- ^ Higham, Nicholas J; Lettington, Matthew (2022). "Optimizing and Factorizing the Wilson Matrix". The American Mathematical Monthly. 129 (5): 454–465. doi:10.1080/00029890.2022.2038006. S2CID 233322415. Archived from the original on 3 March 2022. Retrieved 3 March 2022.
- ^ Edelman, Alan; Murakami, H (April 1995). "Polynomial roots from companion matrix eigenvalues" (PDF). Mathematics of Computation. 64 (210): 763–776. Bibcode:1995MaCom..64..763E. doi:10.1090/S0025-5718-1995-1262279-2. Archived (PDF) from the original on 24 January 2022. Retrieved 2 March 2022.
- ^ Chan, Eunice Y.S.; Corless, Robert M. (6 February 2017). "A new kind of companion matrix". Electronic Journal of Linear Algebra. 32: 335–342. doi:10.13001/1081-3810.3400.
- ^ Corless, Robert M.; Thornton, Steven E. (2017). "The Bohemian Eigenvalue Project". ACM Communications in Computer Algebra. 50 (4): 158–160. doi:10.1145/3055282.3055289. S2CID 34583673. Archived from the original on 1 March 2022. Retrieved 28 February 2022.
- ^ Corless, Robert (2 June 2021). "What can we learn from Bohemian Matrices". Maple Transactions. 1 (1). doi:10.5206/mt.v1i1.14039. S2CID 241595165.
- ^ Chan, Eunice Y.S.; Corless, Robert M.; Gonzalez-Vega, Laureano; Sendra, J. Rafael; Sendra, Juana; Thornton, Steven E. (September 2020). "Upper Hessenberg and Toeplitz Bohemians". Linear Algebra and Its Applications. 601: 72–100. arXiv:1907.10677. doi:10.1016/j.laa.2020.03.037. S2CID 198899515. Archived from the original on 13 August 2023. Retrieved 3 March 2022.
- ^ Fasi, Massimiliano; Negri Porzio, Gian Maria (2020). "Determinants of normalized Bohemian upper Hessenberg matrices". The Electronic Journal of Linear Algebra. 36 (36): 352–366. doi:10.13001/ela.2020.5053. S2CID 191136476.
- ^ Chan, Eunice Y.S.; Corless, Robert M.; Gonzalez-Vega, Laureano; Sendra, J. Rafael; Sendra, Juana (May 2022). "Inner Bohemian Inverses". Applied Mathematics and Computation. 421 (15): 126945. doi:10.1016/j.amc.2022.126945. S2CID 246318540.
- ^ Bogoya, Manuel; Serra-Capizzano, Stefano; Trotti, Ken (2022). "Upper Hessenberg and Toeplitz Bohemian matrix sequences: a note on their asymptotical eigenvalues and singular values" (PDF). Electronic Transactions on Numerical Analysis. 55: 76–91. doi:10.1553/etna_vol55s76. S2CID 243772914. Archived (PDF) from the original on 3 March 2022. Retrieved 3 March 2022.
- ^ Hall, Frank J; Li, Zhongshan (2013). Hogben, Leslie (ed.). Sign Pattern Matrices (2nd ed.). Handbook of Linear Algebra: CRC Press. pp. 42-1–42-32.