User:Dc.samizdat/sandbox
This page serves as a testing area and development space for Dc.samizdat at Wikiversity, and is a personal learning resource. You can create your own sandbox. See also: Topic:Templates | Wikiversity:Sandbox | Template:Template sandbox | Category:Category sandbox |
Polyscheme learning project
[edit | edit source]The Polyscheme learning project is intended to be series of articles on the regular polytopes and Euclidean spaces of 4 or more dimensions, that expand the corresponding series of Wikipedia encyclopedia articles to book length with textbook-like treatment of the material, additional learning resources and explanatory notes.
David Christie on Tolkien, to Ira Sandperl (emeritus) on Tolstoy
[edit | edit source]No doubt Tolkien's novels are not as profound as Tolstoy's with respect to our human condition, but Tolkien's address the more general condition of all peoples. He was the first novelist to write about the affairs of many peoples rather than just the comparatively parochial affairs of men. There is an expansive diversity to his interests, which shows his concern to transcend not just the patriarchy, but the humanitarchy. It disproves his critics' claims that his focus is not wide enough to include women, or people of color, or domains of experience (such as sex) which the critics feel are not sufficiently represented in his stories.
Regular convex 4-polytopes
[edit | edit source]{{W:Template:Regular convex 4-polytopes|wiki=W:}}
| Sequence of 6 regular convex 4-polytopes | ||||||
|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | ||
| Name | 5-cell Hyper-tetrahedron |
16-cell Hyper-octahedron |
8-cell Hyper-cube |
24-cell Hyper-cuboctahedron |
600-cell Hyper-icosahedron |
120-cell Hyper-dodecahedron |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} |
| Coxeter mirrors | ||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 |
| Graph | 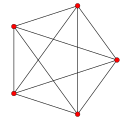
|
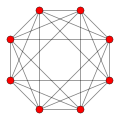
|
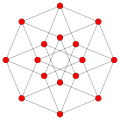
|

|

|

|
| Vertices[a] | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons |
| Cells | 5 {3, 3} | 16 {3, 3} | 8 {4, 3} | 24 {3, 4} | 600 {3, 3} | 120 {5, 3} |
| Tori | 5 {3, 3} | 8 {3, 3} x 2 | 4 {4, 3} x 2 | 6 {3, 4} x 4 | 30 {3, 3} x 20 | 10 {5, 3} x 12 |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells |
| Great polygons | 2 squares x 3[b] | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | |
| Petrie polygons | 1 pentagon x 2 | 1 octagon x 3 | 2 octagons x 4 | 2 dodecagons x 4 | 4 30-gons x 6 | 20 30-gons x 4 |
| Long radius | ||||||
| Edge length[c] | ||||||
| Short radius | ||||||
| Area | ||||||
| Volume | ||||||
| 4-Content | ||||||
| Regular convex 4-polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | |||
| Name | 5-cell
|
16-cell
|
8-cell
|
24-cell | 600-cell
|
120-cell
| |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Coxeter diagram | |||||||
| Graph | 
|

|

|

|

|

| |
| Vertices | 5 | 8 | 16 | 24 | 120 | 600 | |
| Edges | 10 | 24 | 32 | 96 | 720 | 1200 | |
| Faces | 10 triangles |
32 triangles |
24 squares |
96 triangles |
1200 triangles |
720 pentagons | |
| Cells | 5 tetrahedra |
16 tetrahedra |
8 cubes |
24 octahedra |
600 tetrahedra |
120 dodecahedra | |
| Cartesian[d] coordinates |
( 1, 0, 0, 0) (−1/4, √5/4, √5/4, √5/4) (−1/4, √5/4,−√5/4,−√5/4) (−1/4,−√5/4, √5/4,−√5/4) (−1/4,−√5/4,−√5/4, √5/4) |
({±1, 0, 0, 0}) | (±1/2, ±1/2, ±1/2, ±1/2) | ({±1, 0, 0, 0}) (±1/2, ±1/2, ±1/2, ±1/2) |
({±1, 0, 0, 0}) (±1/2, ±1/2, ±1/2, ±1/2) ([±φ/2, ±1/2, ±φ−1/2, 0]) |
||
| Hopf[i] coordinates |
({<2}𝜋, {<30}𝜋/60, {<2}𝜋)120 | ({<4}𝜋/2, {≤1}𝜋/2, {<4}𝜋/2)4 | ({1 3 5 7}𝜋/4, 𝜋/4, {1 3 5 7}𝜋/4)1 | ({<6}𝜋/3, {≤3}𝜋/6, ({<6}𝜋/3)6 | ({<10}𝜋/5, {≤5}𝜋/10, ({<10}𝜋/5)5 | ({<10}𝜋/5, {≤5}𝜋/10, {<10}𝜋/5)1 | |
| Long radius[j] | 1 | 1 | 1 | 1 | 1 | 1 | |
| Edge length | √5/√2 ≈ 1.581 | √2 ≈ 1.414 | 1 | 1 | 1/ϕ ≈ 0.618 | 1/√2ϕ2 ≈ 0.270 | |
| Short radius | 1/4 | 1/2 | 1/2 | √2/2 ≈ 0.707 | 1 - (√2/2√3φ)2 ≈ 0.936 | 1 - (1/2√3φ)2 ≈ 0.968 | |
| Area | 10•√8/3 ≈ 9.428 | 32•√3/4 ≈ 13.856 | 24 | 96•√3/8 ≈ 20.785 | 1200•√3/8φ2 ≈ 99.238 | 720•25+10√5/8φ4 ≈ 621.9 | |
| Volume | 5•5√5/24 ≈ 2.329 | 16•1/3 ≈ 5.333 | 8 | 24•√2/3 ≈ 11.314 | 600•1/3√8φ3 ≈ 16.693 | 120•2 + φ/2√8φ3 ≈ 18.118 | |
| 4-Content | √5/24•(√5/2)4 ≈ 0.146 | 2/3 ≈ 0.667 | 1 | 2 | Short∙Vol/4 ≈ 3.907 | Short∙Vol/4 ≈ 4.385 | |
Scratch
[edit | edit source]400 hexagons
In each hemi-icosahedron, 15 edges come from 10 disjoint 5-cells each contributing 4 edges to this hemi-icosahedron, and 3 hemi-icosahedra fitting together around each edge sharing it, as Grünbaum discovered they do. One other hemi-icosahedron fits against each of 10 hemi-icosahedron faces, and two other hemi-icosahedra fit around each of 15 opposite edge, all the same set of 11 hemi-icosahedra.
Coordinate systems on the 3-sphere
[edit | edit source]The four Euclidean coordinates for S3 are redundant since they are subject to the condition that x02 + x12 + x22 + x32 = 1. As a 3-dimensional manifold one should be able to parameterize S3 by three coordinates, just as one can parameterize the 2-sphere using two coordinates (such as latitude and longitude). Due to the nontrivial topology of S3 it is impossible to find a single set of coordinates that cover the entire space. Just as on the 2-sphere, one must use at least two coordinate charts.
Hopf coordinates of the regular convex 4-polytopes
[edit | edit source]As with Cartesian coordinates, there are multiple reference frames which give useful Hopf coordinates.[h] One can choose any of the 4-polytope's great circle polygons for the 𝜉i coordinate to range over; then the 𝜉j coordinate will range over the vertices of whatever kind of great circle polygon lies orthogonal to the 𝜉i great circle plane. Note that the 𝜉j polygon will sometimes be a digon (a great circle plane intersecting only 2 vertices), as in the case of the the planes orthogonal to the 24-cell's hexagonal planes. The choice of polygons will (almost) determine the only possible range for the 𝜂 coordinate; the only remaining variable is the multiplicity 𝓂 of the coordinates.
| Hopf coordinates[i] of the regular convex 4-polytopes | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5-cell | 16-cell | 8-cell | 24-cell | 600-cell | 120-cell | |||||||
| Digons | ({<2}𝜋, {<30}𝜋/60, {<2}𝜋)120 | ({<2}𝜋, {<150}𝜋/300, {<2}𝜋)1 | ||||||||||
| Squares | ({<4}𝜋/2, {≤1}𝜋/2, {<4}𝜋/2)4 | ({<4}𝜋/2, {≤1}𝜋/2, {<4}𝜋/2)4 ({1 3 5 7}𝜋/4, 𝜋/4, {1 3 5 7}𝜋/4)1 |
({<4}𝜋/2, {<15}𝜋/30, {<4}𝜋/2)2 | ({<4}𝜋/2, {<75}𝜋/150, {<4}𝜋/2)2 | ||||||||
| Rectangles | ({1 3 5 7}𝜋/4, 𝜋/4, {1 3 5 7}𝜋/4)1 | Pentagons | ({0 2 4 6 8}𝜋/5, {<24}𝜋/48, {1 3 5 7 9}𝜋/5)5 | ({0 2 4 6 8}𝜋/5, {<24}𝜋/48, {1 3 5 7 9}𝜋/5)1 | ||||||||
| Hexagons | ({<6}𝜋/3, {≤1}𝜋/2, {<2}𝜋)1 | ({<6}𝜋/3, {<5}𝜋/10, {<4}𝜋/2)1 | ({<6}𝜋/3, {≤24}𝜋/48, {<4}𝜋/2)1 | |||||||||
| ({<6}𝜋/3, {≤3}𝜋/6, ({<6}𝜋/3)6 | ({<6}𝜋/3, {<10}𝜋/20, ({<6}𝜋/3)3 | ({<6}𝜋/3,{<50}𝜋/100,{<6}𝜋/3)3 | ||||||||||
| Decagons | ({<10}𝜋/5, {≤1}𝜋/2, {<6}𝜋/3)1 | ({<10}𝜋/5, {<10}𝜋/20, {<6}𝜋/3)1 | ||||||||||
| ({<10}𝜋/5, {≤5}𝜋/10, ({<10}𝜋/5)5 | ({<10}𝜋/5,{≤5}𝜋/10,{<10}𝜋/5)1 | |||||||||||
| 30-gons | ({<30}𝜋/15,{≤15}𝜋/30,{<30}𝜋/15)24 | |||||||||||
Great circle digons of the 5-cell
[edit | edit source]One set of Cartesian origin-centered coordinates for the 5-cell can be seen as a hyperpyramid with a regular tetrahedral base in 3-space, with edge length 2√2 and radius √3.2:
( 4/√5, 0, 0, 0)
(−1/√5, 1, 1, 1)
(−1/√5, 1,−1,−1)
(−1/√5,−1, 1,−1)
(−1/√5,−1,−1, 1)
Rescaled to unit radius and edge length √5/√2 these coordinates are:
( 1, 0, 0, 0)
(−1/4, √5/4, √5/4, √5/4)
(−1/4, √5/4,−√5/4,−√5/4)
(−1/4,−√5/4, √5/4,−√5/4)
(−1/4,−√5/4,−√5/4, √5/4)
| Great circle digons of the 5-cell Cartesian ({ , , , }) | |||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Great squares of the 16-cell
[edit | edit source]
| ||||||
| ||||||
The 8 vertices of the 16-cell lie on the 4 coordinate axes and form 6 great squares in the 6 orthogonal central planes. The Cartesian axes lie on the diagonals of the square tables, which resemble the great squares. Rotate the tables 45 degrees clockwise for a vertex up orientation, and another 90 degrees for the standard xy orientation.
By convention rotations are always specified in two completely orthogonal invariant planes xy (whose vertices are numbered counterclockwise by 𝜉xy) and wz (whose vertices are numbered counterclockwise by 𝜉wz). The rotation in the xy plane does not move points in the wz plane, and vice versa. In the 16-cell these two simple rotations rotate disjoint sets of 4 vertices each (because completely orthogonal planes intersect only at the origin and share no vertices). The 𝜂 coordinate of the 4 vertices in the xy plane is 0 and the 𝜂 coordinate of the 4 vertices in the wz plane is 1 (𝜋/2). The w and z coordinates of the vertices in the xy plane are 0 regardless of the rotational position of the wz plane (the 𝜉wz coordinate), and the x and y coordinates of the vertices in the wz plane are 0 regardless of the rotational position of the xy plane (the 𝜉xy coordinate).
| Great squares of the 16-cell Cartesian ({0, ±1, 0, 0}) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Great rectangles (60 degree planes) of the 8-cell
[edit | edit source]None of the 8-cell's 16 vertices lie in the 6 orthogonal central planes. The "north pole" is not a vertex, and 0 does not appear as a value in any (Hopf or Cartesian) coordinate.
Each of the 8-cell's eight √4 long diameters joining two antipodal vertices lies 45 degrees (𝜋/4) off each of the 4 Cartesian coordinate axes. The Hopf 𝜼 coordinate is 𝜋/4 for all the vertices, and the 𝜉xy and 𝜉wz coordinates are even and odd multiples of 𝜋/4 respectively.
Although the 16 vertices do not lie in the 6 orthogonal central planes, they do lie (by fours) in central planes, but the central polygons they form are rectangles (not squares), and the planes are inclined at 60 degrees (𝜋/3) to each other and to the orthogonal central planes. These 16 great rectangles measure √1 by √3, and their √1 edges are opposite pairs of 8-cell edges. Their √3 edges are interior chords of the 8-cell: long diagonals of the 8 cubic cells.[k]
Because there is only one 𝜼 coordinate value, only one table is required, but note that the table is not a great square but a duocylinder (its opposite edges are identified).[l] Each row, column or diagonal in the table is a great rectangle.
| Great rectangles (60 degree planes) of the 8-cell
Cartesian (±1/2, ±1/2, ±1/2, ±1/2) | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||
Great squares and rectangles of the 24-cell
[edit | edit source]The great square coordinates of the 16-cell (above), combined with the great rectangle coordinates of the 8-cell (above), comprise a set of coordinates for the 24-cell. Because the 16-cell lies vertex-up in this coordinate system, so does the 24-cell.
Great squares of the 24-cell
[edit | edit source]Another useful set of coordinates for the 24-cell is comprised solely of orthogonal great squares. In this coordinate system the 24-cell lies cell-up, and the great squares are aligned with the squares of the coordinate lattice.
| Great squares of the 24-cell Cartesian (±√1/2, ±√1/2, 0, 0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Great squares and rectangles of the compound of dual 24-cells
[edit | edit source]Two sets of coordinates for the 24-cell have now been given (above). In the first (great squares and rectangles) the 24-cell lies vertex-up, and in the second (great squares only) it lies cell-up. The 24-cell being a self-dual 4-polytope, these two 24-cells are duals of each other, the vertices of one lying at the cell centers of the other, and the union of their two sets of coordinates is a 48-vertex compound of duals of the same radius.
In this compound of two 24-cells, 24 16-cells are inscribed: the 3 inscribed in each of the dual 24-cells, and 18 others which span the two 24-cells.[2] Each of these 24 16-cells, with its 4 orthogonal axes and 6 orthogonal planes, constitutes an equivalent basis for a Cartesian coordinate system, and contains three pairs of completely orthogonal planes, each pair of which intersects all 8 of the 16-cell's vertices. The compound of two 24-cells has 24 axes and 24 bases, with each basis consisting of four axes and each axis occurring in four bases.
The 3 16-cells inscribed in each 24-cell are disjoint from each other and the dual 24-cell's 3 inscribed 16-cells. Each 24-cell has 18 central squares, and the 18 spanning 16-cells are each comprised of 4 vertices comprising a great square from one of the 24-cells, and another 4 vertices comprising a great square from the dual 24-cell.[m]
Great hexagons and squares of the compound of dual 24-cells
[edit | edit source]In a single 24-cell, the hexagonal central planes lie at 60 degrees to each other and to the square central planes. The central planes orthogonal to the hexagonal planes are digons: they intersect only 2 vertices. Consequently it is not possible to find Hopf coordinates for the 24-cell in which both the 𝜉i and 𝜉j orthogonal invariant planes contain hexagons.
However, the 24-cell and its unscaled dual form a compound in which the dual 24-cells are separated by a Clifford displacement (an isoclinic rotation) of 30 degrees. The hexagonal planes are still not orthogonal to each other in this compound (they are inclined at 30 degrees or 60 degrees to each other), so it is still impossible to find a 6 x 6 array of Hopf coordinates, but the hexagonal planes of one 24-cell are orthogonal to the square planes of the other. In this compound of 48 vertices, a hexagonal wz plane and a square xy plane can be the invariant planes of a 6 x 4 array of Hopf coordinates.
| Great hexagons and squares of the compound of dual 24-cells
Cartesian (±_, ±_, _, _) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Great hexagons and digons of the 24-cell
[edit | edit source]| Great hexagons and digons of the 24-cell
Cartesian (±_, ±_, _, _) | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||
|
Great hexagons and squares of the 24-cell
[edit | edit source]| Great hexagons and squares of the 24-cell
Cartesian (±_, ±_, _, _) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dual fibrations
[edit | edit source]Each set of similar great circle polygons (squares or hexagons or decagons) can be divided into bundles of non-intersecting Clifford parallel great circles (of 30 squares or 20 hexagons or 12 decagons).[n] Each fiber bundle of Clifford parallel great circles is a discrete Hopf fibration which fills the 600-cell, visiting all 120 vertices just once.
| Great circle decagons and hexagons of the 600-cell Hopf ({<6}𝜋/3, {<10}𝜋/20, {<2}𝜋)1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Great circle pentagons of the 600-cell
[edit | edit source]| Great circle pentagons of the 600-cell Cartesian ({0, ±1, 0, 0}) (±1/2, ±1/2, ±1/2, ±1/2) ([±φ/2, ±1/2, ±φ−1/2, 0]) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Great circle squares and hexagons of the 120-cell
[edit | edit source]| Great circles of the 120-cell: Hopf ({<6}𝜋/3, {≤24}𝜋/48, {<4}𝜋/2)1 |
|---|
Great circle decagons and hexagons of the 600-cell
[edit | edit source]| Great circle decagons and hexagons of the 600-cell: Hopf ({<10}𝜋/5, {≤1}𝜋/2, {<6}𝜋/3)1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Great circle decagons of the 600-cell
[edit | edit source]| Great circle decagons of the 600-cell: Hopf ({0 1 2 3 4 5 6 7 8 9}𝜋/5, {0 1 2 3 4 5}𝜋/10, {0 1 2 3 4 5 6 7 8 9}𝜋/5)5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bϕ/2 ≈ 0.769 ab ≈ 0.559 bϕ-1/2 ≈ 0.294 b2 ≈ 0.905 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Equilateral rings
[edit | edit source]Equilateral rings are those which can be constructed out of equilateral triangles on the circumference of a sphere.
Borromean equilateral rings
[edit | edit source]The {1,1,1} torus knot.
The vertices of the regular icosahedron form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings. In a Jessen's icosahedron of unit short radius one set of these three rectangles (the set in which the Jessen's icosahedron's long edges are the rectangles' long edges) measures . These three rectangles are the shortest possible representation of the Borromean rings using only edges of the integer lattice.
...
Kinematics
[edit | edit source]In 3D we have the kinematic transformations of the cuboctahedron (cuboctahedron, icosahedron, jessen's, golden icosa?, octahedron-2, tetrahedron-4?) and their duals, the transformations of the dodecahedron: two sets of nesting Russian dolls (or perhaps one set?). In 4D we apparently have instances of the cuboctahedron nestings in the 600-cell (and perhaps the dodecahedron nestings as well, in the 120-cell?). This suggests that the unit-radius sequence of 4-polytopes may contain dynamic as well as static nestings.
From Kinematics of the cuboctahedron § Duality of the rigid-edge and elastic-edge transformations:
Finally, both transformations are pure abstractions, the two limit cases of an infinite family of cuboctahedron transformations in which there are two elasticity parameters and no requirement that one of them be 0. ... In engineering practice, only a tiny amount of elasticity is required to allow a significant degree of motion, so most tensegrity structures are constructed to be "drum-tight" using nearly inelastic struts and cables. A tensegrity icosahedron transformation is a kinematic cuboctahedron transformation with reciprocal small elasticity parameters.
From 24-cell § Double rotations:
The points in the completely orthogonal central plane are not constrained to be fixed. It is also possible for them to be rotating in circles, as a second invariant plane, at a rate independent of the first invariant plane's rotation: a double rotation in two perpendicular non-intersecting planes of rotation at once.[q] In a double rotation there is no fixed plane or axis: every point moves except the center point. The angular distance rotated may be different in the two completely orthogonal central planes, but they are always both invariant: their circularly moving points remain within the plane as the whole plane tilts sideways in the completely orthogonal rotation. A rotation in 4-space always has (at least) two completely orthogonal invariant planes of rotation, although in a simple rotation the angle of rotation in one of them is 0.
This suggests that the reciprocal limit-case kinematic transformations (with one orthogonal elasticity parameter or the other equal to 0) may be expressable as double rotations, considering the relativity of such transformations.[r]
Completely orthogonal planes
[edit | edit source]In three dimensions (on polyhedra) there are no disjoint great circles. Every pair of great circles intersects at two points, the endpoints of a diameter of the sphere. But in four dimensions (on polychora) every great circle is disjoint from exactly one other great circle: the one to which it is completely orthogonal.
If we consider the two polyhedral great circles' common diameter to be a common axis of rotation, we can see that rotating either circle about that axis generates the whole polyhedron; thus either circle by itself can generate the whole polyhedron by rotation. But in four dimensions two completely orthogonal great circles have no common axis of rotation (no points at all in common, all their points are disjoint). Clearly either circle by itself cannot generate the entire polychoron by rotation about a fixed axis. Rotating each circle about an axis generates only half the points on the 3-sphere - rotating the other circle generates the other half of them. Rotation about a fixed axis in four dimensions necessarily leaves an entire plane fixed, and generates only a 3-dimensional polyhedron. If the great circle in the xy plane is rotated about the y axis, only a 2-sphere is generated, and all the points on the 3-sphere outside the hyperplane w = 0 will be left out.
In the 24-cell and the 8-cell, which are radially equilateral, ...
Motion
[edit | edit source]What does it mean to say that an object moves through space? Coxeter group theory provides precise answers to questions of this kind. A rigid object (polytope) moves by distinct transformations, changing itself in each discrete step into a congruent object in a different orientation and position.
Coxeter mirrors
[edit | edit source]Coxeter group theory (the mathematics of polytopes of any number of dimensions) can be informally described as a finite closed system of mirrors, or the geometry of multiple mirror images. Mathematically it is the equivalent of the theory of finite reflection groups and root systems, expressed in a different mathematical language. But unlike those group theory languages, its principal objects can be defined in the most intuitive and elementary way:
Imagine a few (semi-transparent) mirrors in ordinary three dimensional space. Mirrors (more precisely, their images) multiply by reflecting in each other, like in a kaleidoscope or a gallery of mirrors. A closed system of mirrors is what we see when we look into such a kaleidoscope.[5]
Coxeter refers to the space between two parallel mirrors as "the region of possible objects". This suggests that space itself is being generated by the objects that it contains, which parallel reflections multiply infinitely. When the mirrors are not parallel, the multiplication may be finite rather than infinite (provided the dihedral angle between the mirrors is a submultiple of 𝝅). The space between two or more such intersecting mirrors is called the fundamental region, and it constitutes a proto-space of a finite number of dimensions with mirrors as its bounding walls. Coxeter says "the lines of symmetry or circles of symmetry or planes of symmetry are mirrors reflecting the whole pattern into itself. We count these circles of symmetry by counting their pairs of antipodal points of intersection with a single equator."[6] He characterizes great circles of symmetry in terms of the Petrie h-gon i.e. the 3h/2 circles of symmetry possessed by each Platonic solid. For example the Petrie polygon of the octahedron and the cube is the hexagon, so they have 18/2 = 9 great circle planes of symmetry (mirrors). Each is generated by placing a single point-object in the fundamental region (off the surface of any mirrors); reflected in the mirrors it multiplies into all the vertices of the polytope.
Translation-rotations
[edit | edit source]An object displacement in space may be a rotation (which leaves at least one point invariant), a translation (which does not), or a combination of both.[7] The circular path of a rotation may be combined with a translation in the axial direction of the rotation yielding a screw-displacement, the general case of a displacement.[8] In three dimensions, a screw-displacement is a simple helix, as its name suggests. In four dimensions, the circular path of an isoclinic rotation is already a helix (a geodesic isocline), and there are four orthogonal axial directions of rotation.[9] In the unit-radius 24-cell an isoclinic rotation by 60° moves each vertex √3/4 ≈ 0.866 in each of four orthogonal directions at once, a total Pythagorean distance as if it had moved straight along a combined √3 ≈ 1.732 chord. When the rotation is combined with a unit translation, the √1 translation vector must be divided among all four rotation vectors. The vertex moves √3/4 + 1/4 = √1 in each of the four orthogonal directions, moving a combined Pythagorean distance of √4, the maximum unit displacement in 4 dimensions: the distance which is the long diameter of the 4-hypercube (tesseract). This movement could take the vertex to its antipodal vertex √4 away, if the direction of the translation is so aligned, but in all other cases it will take it to a point outside the 24-cell.
Relative screw displacement
[edit | edit source](screw displacement) QT = QR2 = R4 = Q2 (double rotation)[10]
A screw displacement in four dimensions is equivalent to a double rotation, by the principle of relativity. There are only two kinds of screw displacements possible in only four dimensions: the single kind (which also occurs in three dimensions), and the double kind (which requires four dimensions). The latter kind of screw displacement is inherently double, the product of 4 reflections, just like a double rotation. In fact it is just a double rotation, seen from a moving inertial reference frame.
A product of two reflections is a (simple) rotation, unless the reflecting facets are exactly parallel, in which case it is a translation. In other words, a translation is just a rotation on a circle of infinitely long radius (a straight line). A screw displacement is just a double rotation in which one rotation (the one which is the translation) has infinitely long radius, i.e. a vanishingly small angle of rotation (near 0 degrees) compared to the angle of the other rotation (between 0 and 90 degrees). The screw displacement looks like a simple rotation within a three dimensional reference frame that is in uniform translation on the 4th dimension axis at near-infinite velocity. In the case of actual moving objects, no actual translation is an infinite straight line, and no velocity is infinite; any moving object that describes a screw-displacement is presumably moving on a curved translation under the influence, at least, of some distant gravitational force, however miniscule, and the radius of the translation-rotation it describes is merely very long, not infinite. So we can say that there can be only one range of situations in actuality, no perfectly straight translations but only double rotations of more or less eccentricity, which will appear to be simple rotations inside a 3-dimensional reference frame moving uniformly along the 4th dimension "translation" axis. Its eccentricity is merely a matter of choice of reference frame: it looks like a simple rotation in a reference frame moving uniformly with the translation, and a double rotation (of perhaps extreme eccentricity) in a reference frame that is not moving with the translation.
Within this range of possibilities, only one possibility is not eccentric: the case of the equi-angled double rotation, called an isoclinic rotation or Clifford displacement. Since the ratio of eccentricity is a matter of choice of reference frame, we may adopt as our preferred reference frame (of any actual screw displacement occuring in practice) the inertial reference frame in which the double rotation is isoclinic.
Total internal reflection
[edit | edit source]The phenomenon in physics known as total internal reflection keeps light confined within one strand of a fiber optic cable. Isoclinic rotations and screw displacements in 4-dimensional space are both the consequence of four symmetrical reflections, and their propagation corresponds to a total internal reflection within the 3-sphere. Consequently 4-dimensional space itself acts as a waveguide for isoclinically rotating objects during their translation. This provides a purely geometric model for the inertia of mass-carrying objects, and for light-wave propagation.
Isoclines
[edit | edit source]In an isoclinic rotation the vertices of a 4-polytope such as the 24-cell move on isoclines, which are helical circles that wind through all four dimensions. Isoclinic rotations are chiral, occuring in left-handed and right-handed mirror-image pairs in which the moving vertices reach different destinations along left or right paths. The isoclines themselves however (the helical paths of the moving vertices) are not chiral objects: they are non-twisted (directly congruent) circles, of a special 4-dimensional kind. Every left isocline path in a left-handed rotation acts also as a right isocline path in some right-handed rotation, in some other left-right pair of isoclinic rotations. Isoclinic rotations and their isoclines occur as fibrations (fiber bundles of non-intersecting but interlinked circles), with each fibration consisting of a single distinct left-right pair of isoclinic rotations. Each distinct left (or right) rotation has some number of isoclines, which are the circular paths along which its vertices orbit, with each vertex confined to a single isocline circle throughout the rotation. The multiple isoclines of a distinct left or right rotation do not intersect each other; they are Clifford parallel, which means that they are curved lines which are parallel to each other, in the sense that they are the same distance apart at all of their corresponding (nearest) points. Thus the moving vertices in an isoclinic rotation circulate in parallel disjoint sets.
In the 24-cell's characteristic kind of isoclinic rotation, the moving vertices circulate on skew hexagon isoclines, in 4 parallel disjoint sets of 6 moving vertices each. This characteristic kind of isoclinic rotation occurs in four different fibrations: there are four distinct left-right rotation pairs. In each distinct left (or right) rotation, there are 4 Clifford parallel isoclines, each of which is a helical circle through 6 vertex positions. The 4 disjoint circles of 6 vertices pass through all 24 vertices of the 24-cell, just once. Although the four isocline circles do not intersect, they do pass through each other as do the links of a chain, but unlike linked circles in three-dimensional space, they all share the same center point.
Polygrams and cell rings
[edit | edit source]The isoclines of 24-cell isoclinic rotations in hexagonal central planes have 6 chords which form a skew hexagram. Every hexagram isocline is contained within the volume of a distinct ring of 6 face-bonded octahedral cells which, like its axial great circle hexagon is an equatorial ring of the 24-cell. Each 6-cell ring contains the left and right isoclines of a distinct left-right pair of isoclinic rotations. The 6-cell ring itself is not a chiral object because it contains both mirror-image isoclines: they are twisted in opposite directions (around each other), but the 6-cell ring that contains them both has no torsion.
Reflections
[edit | edit source]Because each octahedral cell volume can be subdivided into 48 orthoschemes (the characteristic tetrahedron of the octahedron and of the 24-cell), we can be more precise in describing the cell ring each isocline stays within. Within the 6-cell ring of face-bonded spherical octahedra is a ring of face-bonded spherical characteristic tetrahedra that contains the isocline. Several characteristics of this ring are evident from the nature of characteristic orthoschemes: it consists of alternating left-hand and right-hand orthoschemes (mirror images of each other in their common face), and each of them contains one and only one vertex of the 24-cell.[u] The sequence of orthoscheme vertices is the same as the sequence of isocline vertices, except that it includes the vertices near-missed by the isocline as well as those the isocline intersects (12 distinct vertices instead of 6), and the orthoscheme sequence will have many more than 12 elements because it includes more than two orthoschemes incident to each vertex.[v]
Physical space
[edit | edit source]We attempt to be more precise about the shape of this 4-space, and in particular, the cause of its shape, i.e. the relationship between the fundamental forces observed in nature and this spatial geometry. As Einstein did in his 1923 thought experiment, we identify the observed 3-dimensional cosmos (everything in it up to some large scale such as a galaxy) as a thin manifold embedded in a Euclidean (i.e. flat) 4-dimensional space of the kind elucidated by Coxeter. Further we postulate that every mass-carrying particle in this space is in motion at speed relative to the 4-dimensional space itself.
The 4-space therefore has a quasi-ether-like existence insofar as it defines a field at absolute rest, relative to which the motion of all particles at speed can be universally compared, with the important provision that no particle, anywhere, is ever at absolute rest itself with respect to this field. The condition of absolute rest is an abstract condition attributable only to the field, and never to any tangible object. Thus the field itself (4-dimensional Euclidean space) is an abstraction somewhat more tangible than Mach's relative space, but much less tangible than the luminous ether, much as Einstein found 4-dimensional spacetime to be. Directions and distances can be fixed universally within the Euclidean 4-space field (they are invariant for all observers regardless of their direction of motion within the field), but locations can only be relative to some object (not to the field itself), and all 4-dimensional velocities are invariant: they are always with respect to the field, for any mass-bearing particle or observer.
Einstein's general relativity identifies gravity as a fictitious force, attributable to the shape of the 3-dimensional manifold rather than to an attractive force acting instantaneously at a distance. The 3-dimensional manifold is said to be singular and universal (all objects in the universe lie within it), but its shape varies by location. It is assumed to curve or dimple in the vicinity of massive objects, such that other objects fall into the dimples naturally in the course of following straight-line paths (geodesics) through it. In general relativity 3-dimensional space is flat near each observer, but there is no universally flat space except in regions far removed from massive objects, i.e. in places where the simplifications of the theory of special relativity can be assumed. But in Euclidean relativity this 3-dimensional manifold is embedded in a 4-dimensional Euclidean space, and that 4-space field is flat universally, at all times for all observers. Furthermore, we only assume that the 4-dimensional space is singular and universal; there might be more than one 3-dimensional manifold embedded within it, and the 3-manifolds do not necessarily intersect. In Euclidean relativity we expect that not just gravity, but all the fundamental forces observed in nature, are an expression of the local geometry of a 3-space manifold embedded in Euclidean 4-space. By expression we mean the consequence of a transformation such as a reflection, rotation or translation, i.e. operations of the fundamental Coxeter symmetry groups, which characterize the Euclidean geometry of the universal space in which the 3-space manifolds are embedded.
Closed 3-manifolds embedded in 4-space
[edit | edit source]The only reason to suppose there is only one such closed, curved soap-bubble 3-manifold in our 4-space universe is the assumption that every particle in the universe had a common origin, at a single point in 4-space and a single moment in time in a big bang, and even in that case there could be many such soap-bubble 3-manifolds in existence now. One can certainly model the observed universe as a single closed, curved 3-manifold, and cosmologists do, but there is no more proof that this model is the correct one than there was for the model with the earth at the center of the universe. Whether we determine that light propagates through 4-space in straight lines, or only on geodesic curves along 3-manifolds, we can only determine by looking that the space near us is resolutely 3-dimensional (not admitting the construction of four mutually perpendicular axes, only three). When we look out very far, at distant galaxy clusters for example, we have no way of determining whether we are looking through three dimensional space or four dimensional space. All those distant objects we see might lie in the same 3-manifold (perhaps on the same rough 3-sphere) that we do, but why should they have to? Might they not lie on separate 3-sphere soap bubbles, vastly distant from ours, whether or not all the soap bubbles had a common origin at one place and time?
When we consider the ways in which particles propagating at the speed of light might reach us, considering that we ourselves are formations of particles propagating at the speed of light (all together in almost the same direction), it is clear that we ought not to expect to be overtaken by such particles emanating from stars on the opposite side of our own 3-manifold (from our antipodes, so to speak), because even such a particle redirected exactly backwards along the proper time axis of a star at our antipodes could only follow us along our opposite-direction proper-time axis at a fixed distance forever, never overtaking us, as we travelled in the same direction through 4-space at the same speed forever. Or, since our own path through 4-space is a helical one (as we are engaged in numerous concentric orbits), if the pursuing particle's path through 4-space were a straighter one, it might in principle overtake us eventually, but probably not in our actual experience, and never as a particle moving relative to us at nearly the speed . Therefore we should not expect to receive such particle radiation from the backside stars of our own 3-manifold.
The speed of light
[edit | edit source]So far, however, these considerations can apply only to mass particle radiation, not to light signals, since we have not yet described how light particles (photons) propagate through 4-space. We have suggested that elementary rigid objects propagate themselves by discrete Coxeter transformations,[r] that atomic mass particles are elementary rigid objects in some sense, and that all such particles are transforming at a constant rate in various directions through Euclidean 4-space. But so far, the motion of mass particles is the only kind of motion we have described; we have not given an account of the nature of light signals, or the manner of their propagation, except to observe that light signals propagate through 4-space faster than , as a consequence of the fact that they are observed to propagate through 3-space at speed .
How much faster than must photons be traveling through 4-space, since they appear to be traveling at relative to two observers: one in the reference frame of the electron emitting the photon, and one in the reference frame of the electron absorbing the photon? If both observers are themselves traveling through 4-space at speed as we have stipulated, then even in the case where their direction through 4-space is the same (they are at rest with respect to each other in the same reference frame), a photon that passes between them must travel at speed if it makes the trip in a straight line, or even faster if it zig-zags in some fashion.
Fortunately, this requirement is not at all paradoxical, since in a system of particles translating themselves through 4-space at the rate of transforms per unit time, some things do move faster than speed . A transforming rigid object with a translational motion at rate may simultaneously have an orthogonal rotational motion at rate , such that its component parts (e.g. each vertex of a rotating-translating 4-polytope) may displace themselves in 4-space more than one object-diameter in each discrete transformation; the combined rotating-and-translating velocity through 4-space of a component may be as much as twice the translational velocity of the whole rigid object, rather than , the diagonal of an atomic unit 4-cube rather than its edge length. But the component points of such a rotating rigid object are all traveling in different directions at any instant, and the combined motion of the object as a whole cannot be other than . Therefore a propagating light signal (a photon) is not a rigid atomic object, but some propagation of one of its component parts. Of course this agrees perfectly well with our understanding of photons as emissions of electrons, even if electrons are themselves rigid atomic objects translating themselves through 4-space at the rate of transforms per unit time. The only "paradox" is linguistic in nature: is not the "speed of light", it is the speed of matter (all mass-carrying particles) through 4-space. The actual speed of photons through 4-space is , as opposed to their observed speed through 3-space of .
...
[edit | edit source]A light signal (photon) propagates at speed c relative to either the emitting or the absorbing inertial reference frame (which reference frames are themselves in motion at speed c relative to their common 4-space stationary reference frame, but perhaps in different directions through that 4-space).
How soap bubble 3-manifolds behave in 4-space
[edit | edit source]120 similar 2-sphere soap bubbles (spherical dodecahedra) tiling the 3-sphere, meeting at 120 degrees three-around each edge, and four at each vertex.[11]
Atmospheric 3-membrane
[edit | edit source]What if the 3-space we observe (the visible universe) were filled with a gas, contained in some manner within the (thin) 3-membrane? Like the (thin) atmosphere of the earth (in a 3-dimensional analogy). In fact it is gas-filled, if the 4-space inside and outside the 3-membrane is empty. That difference is precisely what defines the 3-membrane: it is the 4-space which is not empty. It is not continuously full, as it is a cloud of discrete particles like a gas, and the density of particles is very low in most places, but within the 3-membrane it is never zero. The 3-membrane(s) is the surface(s) of 4-polytope(s) with a very large number of vertices (a function of the number of atoms in the universe, if those vertices are enumerated in some manner that includes the universe's plasma matter), and as in any 4-polytope all its elements lie on a 3-dimensional surface (albeit in the case of plasma on a rather inconsequential and rapidly changing 3D surface).
Configurations in the 24-cell
[edit | edit source]
The 12 axes and 16 hexagons of the 24-cell constitute a Reye configuration, which in the language of configurations is written as 124163 to indicate that each axis belongs to 4 hexagons, and each hexagon contains 3 axes.[12] In its most elemental expression, Reye's configuration is a set of 12 lines which intersect at 16 points, forming two disjoint cubes.[x] It has multiple expressions in the 24-cell.[y]
If the proton and neutron are indeed the hybrid fibrations we have identified, on that assumption we can count the number of valid protons and neutrons that can coexist in the same 24-cell at the same time without colliding, and the total number of distinct configurations of multiple nucleons (the number of distinct nuclides) that a single 24-cell can contain. This will not limit the number of distinct nuclides which can exist, because the 24-cell can be compounded in four-dimensional space in several different ways, but it will quantify the number of nuclides which can occupy the first nuclear shell. We might ask of any less minimal configuration of rotations in a single 24-cell whether it in fact corresponds to an integral number of nucleons occupying the same nuclear shell.
A valid maximal hybrid configuration of rotations in the 24-cell would have the largest number of moving vertices possible without collisions (perhaps 24).[z]
...
[edit | edit source]If the particle energies are to be described as the angular momentum of isoclinic rotations of some kind, it is noteworthy that square isoclinic rotations will describe 16-cells, but not (by themselves) the 24-cell. Square isoclinic rotations are associated with the internal geometry of 16-cells: they are the characteristic rotations of the 16-cell. The chords of the single isocline of a square isoclinic rotation (left or right) are the four orthogonal axes of the 16-cell (enumerated twice), and the isocline is a helical circle passing through all 8 vertices of the 16-cell. A left-right pair of square rotations covers all the elements of the 16-cell (including its 18 great squares and its 16 tetrahedral cells). Thus the square isoclinic rotations say all there is to say about the internal geometry of an individual 16-cell, but they have nothing at all to say about how three 16-cells combine to form a 24-cell.
The hexagonal isoclinic rotations, the characteristic rotations of the 24-cell, do describe the whole 24-cell. Their hexagram isoclines wind through all three 16-cells, their √3 chords connecting the corresponding vertices of pairs of disjoint 16-cells. If vertices moving in hexagonal isoclinic rotations are what carries the energy binding the three quarks together (at least in the case of the neutron), each neutron would require at least two vertices moving in hexagonal isoclinic orbits, for the following reason. We attributed electric charge to the chirality of isospin generally, so we may expect hexagonal isoclinic rotations to contribute to the nucleon's total electric charge, even though they are not intrinsic parts of the three quarks, but rather parts of the whole 24-cell. Since the hexagonal orbits span the three 16-cells equally, the contributions of their moving vertices must be of neutral charge overall. Therefore the neutron must possess pairs of left and right hexagonal isoclinic rotations: minimally, one vertex moving on a left hexagram isocline, and one moving on a right hexagram isocline, which cancel each other because they have exactly opposite isospin. They must be a left and a right isocline from the same fiber bundle, corresponding to the left and right rotations of the same set of Clifford parallel invariant hexagonal planes of rotation. Such a pair is a valid kinematic rotation, because left and right hexagram isoclines of the same fibration do not intersect, and so can never collide.[aa]
...
[edit | edit source]The chiral pair of hexagonal rotations combined with the various square rotations will be a valid hybrid rotation provided no vertex in a hexagram orbit ever collides with a vertex in an octagram orbit. The octagram orbits visit all 8 vertices of the 16-cell in which they are confined. In an up quark with the minimum two moving vertices there are 6 empty vertices at any moment in time, leaving room for cross-traffic.
The moving vertex on a hexagram isocline (of which minimally there will be two, a left and a right) will intersect each 16-cell in two places (not antipodal vertices) at different times. If the two moving vertices are antipodal (a moving axis), they will intersect each 16-cell in two axes at different times.
There are valid configurations of this set of minimal hybrid rotations. In up-down-up proton configurations, the 7 moving vertices may be chosen in various ways that avoid collisions. Similarly in down-up-down neutron configurations, there are 6 moving vertices and various valid configurations. These minimal configurations could be are protons and neutrons, or they could be fractional parts of whole nucleons, less minimal configurations of the same kind of hybrid rotation with more moving vertices.
These minimal hybrid rotations fall short of the full fibration symmetry of an ordinary isoclinic rotation in various ways. The hexagonally-rotating vertices visit only 12 of the 24 vertices once.[ab] The two square-rotating vertices in each up 16-cell visit all 8 vertices twice; the one in each down 16-cell visits all 8 vertices once. The two hexagram vertices each rotate through three 16-cells, so even with the best synchronization, there will be an oscillation in the total number of moving vertices in each 16-cell at any one time. In these minimal configurations, the 16-cells and the 24-cell would be strangely unbalanced objects. More generally, any such balance would require solutions to the n-body problem for 7 and 6 bodies, respectively.
We could attempt to remedy these deficiencies by adding more moving vertices on more isoclines, seeking to make nucleons which are hybrid fibrations with at least one moving vertex on each isocline of each kind of fibration. This more balanced configuration with complete fibrations can be achieved with 6 vertices moving on hexagram isoclines, synchronized so that there are two of these moving vertices in each 16-cell at once. The proton (or neutron) will be a valid hybrid fibration of the 24-cell if it is synchronized to avoid collisions, with 6 vertices moving over all 24 vertices on isoclines of hexagonal fibrations (3 on left isoclines, and 3 on right isoclines), and 5 (or 4) vertices moving over all 24 vertices on isoclines of square fibrations (4 (or 2) on right isoclines, and 1 (or 2) on left isoclines).
The up 16-cells already have two vertices moving on octagram isoclines in the minimal configuration, but the down 16-cells have only one. We can add two vertices moving on a chiral pair of isoclines without breaking the charge balance. Adding two such left-right pairs to each down 16-cell leaves the down 16-cell with two up+right and three down−left vertices. It could decay into an up 16-cell (two up+right vertices) by losing the three down−left vertices with a combined unit negative charge, like the electron emitted during beta minus decay. This configuration of a single stable proton (or single unstable neutron) has 9 (or 12) vertices moving on isoclines of square fibrations: 6 (or 6) on right isoclines, and 3 (or 6) on left isoclines.
The fact that a proton and neutron form a stable nuclide suggests that they can occupy the same 24-cell together, where their moving vertices combine to stabilize the down 16-cell. This is possible because there is enough room in each 16-cell for it to contain the essential moving vertices of both an up and a down quark at the same time: two vertices moving on an up+right isocline, plus one vertex moving on a down−left isocline provided it is not the complement of either of the right rotations (because the left-right pair of the same distinct rotation have exactly opposite isospin and would cancel each other's charge contribution). This deuterium configuration of a stable proton-neutron pair has 9 vertices moving on isoclines of square fibrations: 6 on right isoclines, and 3 on left isoclines. It could be created by beta plus decay when two protons are forced to occupy the same 24-cell, during the first step in the proton-proton chain of nucleosynthesis.
Wiki researchers
[edit | edit source]W:User:Cloudswrest/Regular_polychoric_rings, A.P. Goucher (https://cp4space.wordpress.com/2012/09/27/good-fibrations/)
W:User:Tomruen/Uniform_honeycombs
W:User:PAR physicist (stat. mech.) (Hopf coordinates in Rotations in 4-dimensional Euclidean space)
W:User:DGG, David Goodman (wikipedia admin, librarian, expert on scientific publishing and open access to published research, first amendment absolutist)
S.Fedosin e.g. SPФ symmetry, Scale dimension, Model of Gravitational Interaction[13], Hydrogen system, Metric theory of relativity - perhaps begin here[14]
Fibrations
[edit | edit source]Currently titled Visualization, perhaps this section could be renamed and multiple references given for the W:Hopf fibration[ac] re: the 24-cell. But beware similar material by W:User:Cloudswrest and W:User:Tomruen was deleted from the W:Hopf fibration article once for lack of references. [ad]
Marcelis The first illustration below shows a torus surface on which 4 equidistant circles lie, each having 4 equidistant points that are 4 of the 16 vertices of a hypercube in stereographic projection. On the vertical line and the circle lie 4 equidistant points each, completing the 16 vertices of the hypercube to the 24 vertices of a 24-cell.
Curiosities
[edit | edit source]http://vixra.org/pdf/1812.0482v1.pdf perhaps follows Steinbach's polygonal chord relationships
Review
[edit | edit source]Who is this? http://eusebeia.dyndns.org If identified perhaps could put under External links on some 4-polytope pages. Especially 4D Visualization
Marcelis also Macelis's other website
Communities
[edit | edit source]4-space generally
[edit | edit source]Dimensional analogy opinion
[edit | edit source]Words
[edit | edit source]The polygloss Wendy Krieger's glossary of higher-dimensional terms.
Math
[edit | edit source]The Hopf coordinates {1, ξ1, η, ξ2} [Coxeter 1973 p. 216]. Formulas for the conversion of Cartesian coordinates to Hopf coordinates: https://marc-b-reynolds.github.io/quaternions/2017/05/12/HopfCoordConvert.html
In 3D every displacement can be reduced to a single-rotation combined with a translation (a screw-displacement). In 4D every displacement can be reduced to either a double rotation or a a single rotation combined with a translation (a 3D screw-displacement).[Coxeter 1973 p 218]
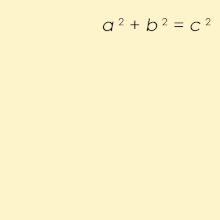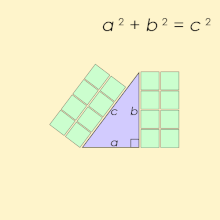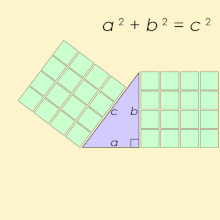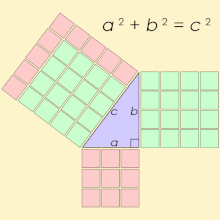
The Icosians and W:Quaternions generally, the "31/2-dimensional coordinates of projective 4-space [google books] Application of quaternions and projective space generally in the vertex figure space (the curved boundary space of a 4-polytope from the inside).
Formula for Vector Rotation in Arbitrary Planes
Viviani's Theorem In an equilateral triangle, the sum of the distances from any interior point to the three sides is equal to the altitude of the triangle
Macelis's other website on the geometrical mathematics of physics.
Truncation
[edit | edit source]What does truncation look like from vertex space (the curved 3-manifold)? Vertices are removed like voids carved out of the interior of the 3-space, or rather, the location of the 3-manifold moves in the 4th direction. How can we imagine observing this (as a continuous process) from the inside of the 3-space?
120-cell
[edit | edit source]"Who ordered that?"[ag]
Omnitruncated 120-cell - the largest uniform convex 4-polytope.
Segerman and Schleimer A first way to understand the combinatorics of the 120–cell is to look at the layers of dodecahedra at fixed distances from the central dodecahedron. A second way to understand the 120–cell is via a combinatorial version of the W:Hopf fibration.
Falsified theory
[edit | edit source]To generate the 120-cell from the 600-cell, it is sufficient to rotate the 600 tetrahedra once, through five positions (either the left-handed or the right-handed chiral rotation). Both chiral rotations are not required, because each 5-click rotation by itself generates all the cells of five disjoint 600-cells, which together comprise all the vertices of the 120-cell and all ten 600-cells. In other words, the two ways to pick five disjoint 600-cells (out of the ten distinct 600-cells) correspond to the two sets of opposing tetrahedra in each dodecahedron. FALSIFIED[16]
Dodecahedron coordinates
[edit | edit source]The red vertices lie at (±φ, ±1/φ, 0) and form a rectangle on the xy-plane. The green vertices lie at (0, ±φ, ±1/φ) and form a rectangle on the yz-plane. The blue vertices lie at (±1/φ, 0, ±φ) and form a rectangle on the xz-plane. (The red, green and blue coordinate triples are circular permutations of each other.)
30-tetrahedron rings are duals of Petrie polygons
[edit | edit source]Talk:Boerdijk–Coxeter helix#30-tetrahedron rings are duals of Petrie polygons
600-cell
[edit | edit source]Rotations
[edit | edit source]In the 600-cell, there is a simple rotation which will take any vertex directly to any other vertex, also moving most of the other vertices but leaving at most 10 other vertices fixed (the vertices that the fixed central plane intersects). The vertex moves along a great circle in the invariant plane of rotation between adjacent vertices of a great decagon, a great hexagon, a great square or a great digon, and the completely orthogonal fixed plane intersects 0 vertices, 2 vertices (a digon), 4 vertices (a square), or 6 vertices (a hexagon), respectively.
Misc
[edit | edit source]The 120 vertices can be seen as the vertices of four sets of 6 orthogonal equatorial pentagons which intersect only at their common center.[ah][ai]
The 600 tetrahedral cells can be seen as the result of a 5-fold subdivision of 24 octahedral cells yielding 120 tetrahedra, in a compound made of 5 such subdivided 24-cells (rotated with respect to each other in angular units of 𝜋/5).
The 600-cell's edge length is ~0.618 times its radius (the 24-cell's edge length). This is 𝚽, the smaller of the two golden sections of √5. Its reciprocal, the larger golden section, is φ = 1.618. A √5 chord will not fit in a polytope of unit radius (√4 diameter), but both of its golden sections will fit, and both occur as vertex chords of the unit-radius 600-cell: the smaller 𝚽 as its edge length, and the larger φ as the chord joining vertices that are 3 edge lengths apart.
In the 24-cell, the 24 vertices can be accounted for as the vertices of (any one of 4 sets of) 4 orthogonal hexagons which intersect only at their common center. In the 600-cell, with 5 inscribed 24-cells, 5 such disjoint sets of 4 orthogonal hexagons will account for all 120 vertices.
In the 24-cell, the 24 vertices can be accounted for as the vertices of (any one of 3 sets of) 6 orthogonal squares which intersect only at their common center. In the 600-cell, with 5 inscribed 24-cells, 5 disjoint sets of 6 such orthogonal squares will account for all 120 vertices.
Notice the pentagon inscribed in the decagon. Its √1.𝚫 edge chord falls between the √1 hexagon and the √2 square. The 600-cell has added a new interior boundary envelope (of cells made of pentagon edges, evidently dodecahedra), which falls between the 24-cells' envelopes of octahedra (made of √1 hexagon edges) and the 8-cells' envelopes of cubes (made of √2 square edges). Consider also the √2.𝚽 = φ and √3.𝚽 chords. These too will have their own characteristic face planes and interior cells, and their own envelopes, of some kind not found in the 24-cell.[ak] The 600-cell is not merely a new skin of 600 tetrahedra over the 24-cell, it also inserts new features deep in the interstices of the 24-cell's interior structure (which it inherits in full, compounds five-fold, and then elaborates on).
evidently the 600-cell has dodecahedra in it
golden triangles[al]
Rotations
[edit | edit source][am] Each isoclinic rotation occurs in two chiral forms: there is a Clifford parallel 24-cell to the left of each 24-cell, and another Clifford parallel 24-cell to its right. The left and right rotations reach different 24-cells; therefore each 24-cell belongs to two different sets of five disjoint 24-cells.
Central planes
[edit | edit source]All the geodesic polygons enumerated above lie in central planes of just three kinds, each characterized by a rotation angle: decagon planes (𝜋/5 apart in the 600-cell), hexagon planes (𝜋/3 apart in each of 25 inscribed 24-cells), and square planes (𝜋/2 apart in each of 75 inscribed 16-cells).
In a 4-polytope, two different central planes may intersect at a common diameter, as they would in 3-space, or they may intersect at a single point only, at the center of the 4-polytope. In the latter case, their great circles are Clifford parallel.[an] Completely orthogonal[ao] great circles are an example of Clifford parallels, but we can also find non-orthogonal central planes which intersect at only a single point.
Because they share a common center, the two circles are obviously not parallel and separate in the usual way of parallel circles in 3-dimensions; in fact they are connected like adjacent links in a chain, each passing through the other (without intersecting at any points), forming a Hopf link.
Cayley’s Factorization of 4D Rotations
[edit | edit source]Any rotation in ℝ4 can be seen as the composition of two rotations in a pair of orthogonal two-dimensional subspaces. When the values of the rotation angles in these two subspaces are equal, the rotation is said to be isoclinic. Cayley realized that any rotation in ℝ4 can be factored into the commutative composition of two isoclinic rotations.[18]
The elements of the Lie group of rotations in four-dimensional space, SO(4), can be either simple or double rotations. Simple rotations have a fixed plane (a plane in which all the points are fixed under the rotation), while double rotations have a single fixed point only, the center of rotation. In addition, double rotations present at least a pair of invariant planes that are orthogonal. The double rotation has two angles of rotation, α1 and α2, one for each invariant plane, through which points in the planes rotate. All points not in these planes rotate through angles between α1 and α2.
Isoclinic rotations are a particular case of double rotations in which there are infinitely many invariant orthogonal planes, with same rotation angles, that is, α1 = ±α2. These rotations can be left-isoclinic, when the rotation in both planes is the same (α1 = α2), or right-isoclinic, when the rotations in both planes have opposite signs (α1 = −α2). Isoclinic rotation matrices have several important properties:
- The composition of two right- (left-) isoclinic rotations is a right- (left-) isoclinic rotation.
- The composition of a right- and a left-isoclinic rotation is commutative.
- Any 4D rotation can be decomposed into the composition of a right and a left-isoclinic rotation.
Hence both form maximal and normal subgroups. Their direct product is a double cover of the group SO(4), as four-dimensional rotations can be seen as the composition of rotations of these two subgroups, and there are two expressions for each element of the group.
30-gon geodesic
[edit | edit source]The 30-gon vertex-less geodesic of the 600-cell reminds me of another remarkable observation about the central axis of the B-C helix made many years ago by the dutch software engineer and geometry experimenter Gerald de Jong,[ap] on a long-extinct email list called Synergetics that mostly featured discussions of Buckminster Fuller[aq] That list didn't extend to 4-polytopes; the geometry discussed there was about 3-dimensional objects, as it also tended to be on Magnus Wenninger's Polyhedron email list. I can't find an archived copy of the email list with Gerald's post but as I recall he studied the B-C helix (Fuller called it the tetrahelix) in 3 dimensions and observed that it had no single central axis, but rather three central axes that passed through each tetrahedron similarly, hitting the volume center of the tetrahedron and hitting two faces near but not at their center, like three holes punched in the face in a small equilateral triangle surrounding the face center. He called the tetrahedra pierced by the three central axes "tetrahedral salt cellars", a wonderfully evocative image and why I have remembered it (correctly, I hope). It is interesting to see that when the helix is bent in the fourth dimension into a ring, in addition to its period being rationalized and its helical edge-paths being straightened into geodesics, its three center axes also merge into one, which passes through a single point at the center of each face.
Golden triangles
[edit | edit source]The golden triangle is uniquely identified as the only triangle to have its three angles in 2:2:1 proportions.

Golden triangles are found in the nets of several stellations of dodecahedrons and icosahedrons.
Since the angles of a triangle sum to 180°, base angles are therefore 72° each.[1] The golden triangle can also be found in a regular decagon, or an equiangular and equilateral ten-sided polygon, by connecting any two adjacent vertices to the center. This will form a golden triangle. This is because: 180(10-2)/10=144 degrees is the interior angle and bisecting it through the vertex to the center, 144/2=72.[1]

A Kepler triangle is a right triangle with edge lengths in a geometric progression in which the common ratio is √φ, where φ is the golden ratio,[a] and can be written: , or approximately 1 : 1.272 : 1.618.[1] The squares of the edges of this triangle are in geometric progression according to the golden ratio.
Triangles with such ratios are named after the German mathematician and astronomer Johannes Kepler (1571–1630), who first demonstrated that this triangle is characterised by a ratio between its short side and hypotenuse equal to the golden ratio.[2] Kepler triangles combine two key mathematical concepts—the Pythagorean theorem and the golden ratio—that fascinated Kepler deeply, as he expressed:
Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.[3]
Some sources claim that a triangle with dimensions closely approximating a Kepler triangle can be recognized in the Great Pyramid of Giza,[4][5] making it a golden pyramid.
Golden chords
[edit | edit source]The golden chords demonstrate that ϕ is a circle ratio like 𝜋, in fact:
- 𝜋/5 = arccos (ϕ/2)
which is one decagon edge. Inversely:
- ϕ = 1 – 2 cos (3𝜋/5)
which can be seen from the arc length of the √2.𝚽 = ϕ golden chord which is 3𝜋/5, but it was apparently discovered first without recourse to geometry.[20]
Phi is a circle ratio, like Pi Pi = 5 arccos (.5 Phi) Note: The angle of .5 Phi is 36 degrees, of which there are 10 in a circle or 5 of in pi radians. Note: Above formulas expressed in radians, not degrees Alex Williams, MD, points out that you can use the Phi and Fives relationship to express pi as follows: 5arccos((((5^(0.5))*0.5)+0.5)*0.5) = pi Robert Everest discovered that you can express Phi as a function of Pi and the numbers 1, 2, 3 and 5 of the Fibonacci series: Phi = 1 – 2 cos ( 3 Pi / 5)
Golden ratio of chords: Peter Steinbach
- Golden Fields - DPF formula https://www.jstor.org or https://www.tandfonline.com/doi/pdf/10.1080/0025570X.1997.11996494
- Sections Beyond Golden https://archive.bridgesmathart.org/2000/bridges2000-35.pdf
Sacred cut (of octagon) https://archive.bridgesmathart.org/2011/bridges2011-559.pdf
W:George Phillips Odom Jr. discovery of golden section in the mid-edge-bisectors of the tetrahedron (applies to the construction of the 600-cell from the 24-cell via truncation of its central tetrahedra) - also look at the other circle/triangle and sphere/tetrahedra relationships he discovered - footnote his relationship to Coxeter and Conway
Nonconvex regular decagon
[edit | edit source]
The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted or its multiplicative inverse:
So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.
24-cell
[edit | edit source]
Whoever this is has some beautiful illustrations of closely related polytopes e.g.[21]
Marcelis including the gem of the modular universe
Cuboctahedron
[edit | edit source]In the 24-cell, there are 16 great hexagons, and each has one pair of vertices (one diameter) which lies on a Cartesian coordinate system axis (in the vertex-up frame of reference). The 24-cell can be seen as the 24 vertices of four orthogonal great hexagons, each aligned with one of the four orthogonal coordinate system axes, and each contributing 6 disjoint vertices. In four dimensions, the four orthogonal planes do not intersect except at their common center. Each great hexagon does not share any vertices with the 3 other hexagons to which it is orthogonal,[ar] but it shares two vertices with each of the 12 other great hexagons to which it is not orthogonal. Four hexagonal geodesics pass though each vertex.
In the cuboctahedron, there are four great hexagons, but they are not orthogonal. Each intersects with each of the others in two vertices (one diameter), and two hexagons pass through each vertex. (In three dimensions, two planes through a common point intersect in a line, whether they are orthogonal or not.) At most one of the four hexagons can have a pair of vertices (a diameter) which lies on a coordinate system axis. In such a frame of reference, the other two axes pass through the centers of a pair of opposing triangular faces, and through the centers of a pair of opposing edges, respectively.
Geometry
[edit | edit source]Triangles
[edit | edit source]...to be added:
If the dual of the 24-cell of edge length √2 is taken by reciprocating it about its circumscribed sphere, another 24-cell is found which has edge length and circumradius √3, and its coordinates reveal more structure. In this form the vertices of the 24-cell can be given as follows:
The 4 orthogonal planes in which the 8 triangles lie are not orthogonal planes of this coordinate system. The triangles' √3 edges are the diagonals of cubical cells of this coordinate lattice.[as]
The 24 vertices are also the vertices of 96 other triangles of edge length √3 that occur in 48 parallel pairs, in planes one edge length apart. Each plane sections the 24-cell through three vertices but does not pass through the center.[at]
..see 5-cell#Construction: Another set of origin-centered coordinates in 4-space can be seen as a hyperpyramid with a regular tetrahedral base in 3-space, with edge length 2√2:
... obs:
Add coordinate examples to this footnote[au]
Rotations
[edit | edit source]The vertices of a convex 4-polytope lie on the 3-sphere, so alternatively they can be described using 4-dimensional spherical coordinates such as the Hopf coordinates {r, ξ1, η, ξ2}, which reveal more structure.
For the 24-cell of edge length and radius 1, the Hopf coordinates of its vertices can be obtained by permuting the three angle coordinates as follows:
{1, ±𝜋/3, ±𝜋/2, ±2𝜋/3}

in 3D section of a 24-cell (of edge length 2) we can construct a tetrahedron with 2√3 legs descending from a vertex (0,0,2) with its base plane triangle intersecting the 2-sphere at (x,y,-1), but only if we put the base vertices at distances apart less than 2√3, as a 2√2 3 3 isosceles triangle e.g. with these vertices:
(-√2,-1,-1) <--- 2√2 --> ((+√2,-1,-1)) <-- 3 --> (0, (+√3, -1) <-- 3 -->
Apparently the base vertices of the tetrahedron are displaced out of this hyperplane in the 4th dimension so the base edges are foreshortened.
... and eight meet at the volume center of each tesseract cube[av]
Kepler problem
[edit | edit source]
We are apt to be smug about the quaint mythological phantasies of our great forebears, as when we learn that Issac Newton worked for more than 30 years as an alchemist trying to turn base metals into gold, before he was appointed Chancellor of the Exchequer to preside over England's mint of sterling instead. Kepler's astrolabe of Plato's holy solids looks that way to us, like a religious miracle the great astronomer hoped for, before he discovered the real symmetry in his three great conservation laws of motion. It should humble us, then, to find out that he was on to something deeper all along, and make us wonder all the more at his genius, that it was the SO(4) rotational symmetry he glimpsed, which generates those conservation laws by Noether's theorem, and also generates the 4-polytopes that Schläfli would discover on the 3-sphere in 4-space two and a half centuries after Kepler, who somehow imagined them from below, projected on the 2-sphere in 3-space.
Laplace–Runge–Lenz vector
[edit | edit source]the following rescued from W:Laplace–Runge–Lenz vector version of 23:32, 27 November 2006 from which it was removed by WillowW (talk | contribs) at 23:46, 28 November 2006 (the Moebius transform was fun, but needs to go now)
Intuitive picture of the rotations in four dimensions
[edit | edit source]
The simplest way to visualize the particular symmetry of the Kepler problem is through its hodographs, the perfectly circular traces of the momentum vector (Figures 2 and 3). For a given total energy E, the hodographs are circles centered on the py-axis, all of which intersect the px-axis at the same two points, px=±p0 (Figure 3). To eliminate the normal rotational symmetry, the coordinate system has been fixed so that the orbit lies in the x-y plane, with the major semiaxis aligned with the x-axis. Inversion centered on one of the foci transforms the hodographs into straight lines emanating from the inversion center (Figure 4). These straight lines can be converted into one another by a simple two-dimensional rotation about the inversion center. Thus, all orbits of the same energy can be continuously transformed into one another by a rotation that is independent of the normal three-dimensional rotations of the system; this represents the "higher" symmetry of the Kepler problem.
Formatting idioms
[edit | edit source]- 1/2(±φ𝞍ϕ𝜙𝝓𝚽𝛷𝜱, ±1, ±1/φ, 0).
- 360^{\circ}
- denoted
Notes
[edit | edit source]- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named4-polytopes ordered by size and complexity - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedSix orthogonal planes of the Cartesian basis - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namededge length of successor - ↑ The coordinates (w, x, y, z) of the unit-radius origin-centered 4-polytope are given, in some cases as {permutations} or [even permutations] of the coordinate values.
- ↑ The point itself (𝜉i, 𝜂, 𝜉j) does not necessarily lie in either of the invariant planes of rotation referenced to locate it (by convention, the wz and xy Cartesian planes), and never lies in both of them, since completely orthogonal planes do not intersect at any point except their common center. When 𝜂 = 0, the point lies in the 𝜉i "longitudinal" wz plane; when 𝜂 = 𝜋/2 the point lies in the 𝜉j "equatorial" xy plane; and when 0 < 𝜂 < 𝜋/2 the point does not lie in either invariant plane. Thus the 𝜉i and 𝜉j coordinates number vertices of two completely orthogonal great circle polygons which do not intersect (at the point or anywhere else).
- ↑ The angles 𝜉i and 𝜉j are angles of rotation in the two completely orthogonal invariant planes[e] which characterize rotations in 4-dimensional Euclidean space. The angle 𝜂 is the inclination of both these planes from the north-south pole axis, where 𝜂 ranges from 0 to 𝜋/2. The (𝜉i, 0, 𝜉j) coordinates describe the great circles which intersect at the north and south pole ("lines of longitude"). The (𝜉i, 𝜋/2, 𝜉j) coordinates describe the great circles orthogonal to longitude ("equators"); there is more than one "equator" great circle in a 4-polytope, as the equator of a 3-sphere is a whole 2-sphere of great circles. The other Hopf coordinates (𝜉i, 0 < 𝜂 < 𝜋/2, 𝜉j) describe the great circles (not "lines of latitude") which cross an equator but do not pass through the north or south pole.
- ↑ 7.0 7.1 The conversion from Hopf coordinates (𝜉i, 𝜂, 𝜉j) to unit-radius Cartesian coordinates (w, x, y, z) is:
- w = cos 𝜉i sin 𝜂
- x = cos 𝜉j cos 𝜂
- y = sin 𝜉j cos 𝜂
- z = sin 𝜉i sin 𝜂
The "Cartesian north pole" (1, 0, 0, 0) is Hopf (0, 𝜋/2, 0). - w = cos 𝜉i sin 𝜂
- ↑ 8.0 8.1 The Hopf coordinates are triples of three angles:
- (𝜉i, 𝜂, 𝜉j)
- ↑ 9.0 9.1 Hopf spherical coordinates[h] of the vertices are given as three independently permuted coordinates:
- (𝜉i, 𝜂, 𝜉j)𝑚
- (𝜉i, 𝜂, 𝜉j)𝑚
- ↑ The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more 4-content within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 120-cell is the 600-point 4-polytope: sixth and last in the ascending sequence that begins with the 5-point 4-polytope.
- ↑ In the 24-cell we find these 16 central rectangles inscribed in the 16 central hexagons. The 8-cell's great rectangles are the same central planes as the 24-cell's great hexagons, but the 8-cell has only 4 of the 6 hexagon vertices. The 16-point (8-cell) is a 24-point (24-cell) with 8 points (square pyramids) lopped off.
- ↑ For fixed η Hopf coordinates describe a torus parameterized by ξxy and ξwz, with η = π/4 being the special case of the Clifford torus in the xy- and wz-planes. All vertices of the 8-cell lie on the Clifford torus, a "flat" 2-dimensional surface embedded in the 3-sphere. The Clifford torus divides the 3-sphere into two congruent solid tori. In a stereographic projection, the Clifford torus appears as a standard torus of revolution. The fact that it divides the 3-sphere equally means that the interior of the projected torus is equivalent to the exterior, which is not easily visualized.
- ↑ In each of the 18 16-cells, the two central squares from dual 24-cells are orthogonal, but not completely orthogonal. Each is already completely orthogonal to another central square within the same 24-cell (within the same 16-cell), and in 4-space a plane cannot be completely orthogonal to more than one other plane through the same point. Although their two sets of 4 vertices are disjoint, that is not because their square planes are completely orthogonal; rather, their planes intersect in a line, but their vertices remain disjoint because the line of intersection does not pass through any of their vertices.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedClifford parallels - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedhelical geodesic - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedone true circle - ↑ 17.0 17.1 17.2 Any double rotation (including an isoclinic rotation) can be seen as the composition of two simple rotations a and b: the left double rotation as a then b, and the right double rotation as b then a. Simple rotations are not commutative; left and right rotations (in general) reach different destinations. The difference between a double rotation and its two composing simple rotations is that the double rotation is 4-dimensionally diagonal: each moving vertex reaches its destination directly without passing through the intermediate point touched by a then b, or the other intermediate point touched by b then a, by rotating on a single helical geodesic (so it is the shortest path).[o] Conversely, any simple rotation can be seen as the composition of two equal-angled double rotations (a left isoclinic rotation and a right isoclinic rotation),[p] as discovered by Cayley; perhaps surprisingly, this composition is commutative, and is possible for any double rotation as well.[3]
- ↑ 18.0 18.1 18.2 Let Q denote a rotation, R a reflection, T a translation, and let Qq Rr T denote a product of several such transformations, all commutative with one another. Then RT is a glide-reflection (in two or three dimensions), QR is a rotary-reflection, QT is a screw-displacement, and Q2 is a double rotation (in four dimensions). Every orthogonal transformation is expressible as
Qq Rr
where 2q + r ≤ n, the number of dimensions. Transformations involving a translation are expressible as
Qq Rr T
where 2q + r + 1 ≤ n.
For n = 4 in particular, every displacement is either a double rotation Q2, or a screw-displacement QT (where the rotation component Q is a simple rotation). [If we assume the Galilean principle of relativity, every displacement in 4-space can be viewed as either of those, because we can view any QT as a Q2 in a linearly moving (translating) reference frame. Therefore any transformation from one inertial reference frame to another is expressable as a Q2. By the same principle, we can view any QT or Q2 as an isoclinic (equi-angled) Q2 by appropriate choice of reference frame.[s] That is to say, Coxeter's relation is a mathematical statement of the principle of relativity, on group-theoretic grounds.[t]] Every enantiomorphous transformation in 4-space (reversing chirality) is a QRT.[4] Cite error: Invalid<ref>tag; name "transformations" defined multiple times with different content - ↑ 19.0 19.1 Cayley showed that any rotation in 4-space can be decomposed into two isoclinic rotations,[q] which intuitively we might see follows from the fact that any transformation from one inertial reference frame to another is expressable as a rotation in 4-dimensional Euclidean space. Cite error: Invalid
<ref>tag; name "Cayley's rotation factorization into two isoclinic reference frame transformations" defined multiple times with different content - ↑ Notice that Coxeter's relation correctly captures the limits to relativity, in that we can only exchange the translation (T) for one of the two rotations (Q). An observer in any inertial reference frame can always measure the presence, direction and velocity of one rotation up to uncertainty, and can always also distinguish the direction and velocity of his own proper time arrow.
- ↑ In the 24-cell 48 characteristic 4-orthoschemes (5-cells) meet at each of the 24 vertices, and 48 characteristic 3-orthoschemes (tetrahedra) fill each of the 24 octahedral cells. The number of characteristic orthoschemes in a regular polytope is the order of its symmetry group, which for the octahedron is 48, and for the 24-cell is 1152 = 24 * 48.
- ↑ The ring contains more orthoschemes than necessary to contain the isocline, because of our stipulation that all pairs of adjacent orthoschemes be face-bonded. The isocline intersects only a vertex, or only an edge, of some orthoschemes in the face-bonded ring. At each vertex it hits, the isocline passes between two orthoschemes that touch only at that vertex. Near each vertex that it misses, the isocline passes through an edge between two orthoschemes that touch only at that edge.
- ↑ Coxeter's relation correctly captures the limits to relativity, in that we can only exchange the translation (T) for one of the two rotations (Q). An observer in any inertial reference frame can always measure the presence, direction and velocity of one rotation up to uncertainty, and can always also distinguish the direction and velocity of his own proper time arrow.
- ↑ The basic expression of Reye's configuration 124163 of 12 lines and 16 points occurs 12 times in the 24-cell, as the 16 vertices of two opposite (completely orthogonal) cubical cells (in one of the 3 inscribed 8-cells), and the 12 geodesic straight lines (hexagonal great circles) on which the cubes' parallel edges lie (orthogonally in the 3 dimensions of 3-sphere space, embedded in a Euclidean space of 4 orthogonal dimensions).
- ↑ An expression of Reye's configuration 124163 with respect to isoclinic rotations of the rigid 24-cell: 12 points are reached by 4 half hexagram isoclines in each left or right 360 degree isoclinic rotation characteristic of the 24-cell, and each of the 16 half hexagram isoclines in the left and right 360 degree rotations reaches 3 points.
- ↑ The valid maximal configurations do have 24 moving vertices. They include a configuration with 12 vertices rotating within each of the three 16-cells on 4 octagram isoclines of the same chirality (while remaining within 4 Clifford parallel moving square planes), and visiting all 8 vertices of each 16-cell in each double revolution. The same maximal configuration also has 12 vertices rotating among the three 16-cells on 4 hexagram isoclines (two left-right pairs) while remaining within 4 Clifford parallel moving hexagonal planes, and visiting all 24 vertices of the 24-cell in each double revolution.
- ↑ Most, but not all, left and right pairs of isoclinic rotations have isocline pairs which are Clifford parallel and visit disjoint vertex sets. The exception is left and right square isoclinic rotations. Their left and right octagram isoclines do intersect, and they each visit the same set of 8 vertices.
- ↑ Each hexagonal fibration has a right isoclinic rotation on 4 Clifford parallel right hexagram isoclines, and a corresponding left rotation on 4 Clifford parallel left hexagram isoclines, in the same set of 4 Clifford parallel invariant hexagonal planes. The right and left rotations reach disjoint sets of 12 vertices.
- ↑ On a 2-sphere (globe), if you go off in any direction and keep going straight you eventually arrive back at your starting point. Same with the 3-sphere, except you are no longer restricted to a plane, you can go off in any 3-dimensional direction. For the 2-D case all great circles intersect. You can avoid this for the 3-D case. Step away from your initial starting point and go off in a new direction. You want to pick this direction so that you don't intersect the previous geodesic. To this end you have to give your new direction a little "skew" so that your new starting direction is not exactly parallel, and out of the plane, to your old direction. This avoidance of intersection causes the two loops/geodesics to spiral around each other and/or interlock. For the Hopf fibration the farther away you are from the initial starting point, the more "skew" you add. When you are 90 degrees away, you add 90 degrees of skew. This is the most extreme case and you have two interlocking rings passing through the midpoint of the other ring. With this construction you can parameterize the whole 3-sphere, with no two rings ever touching each other. ---- W:User:Cloudswrest in Talk:Hopf fibration
- ↑ This section was deleted for lacking references. I had been adding some graphics. I copied the section to User:Tomruen/Regular polychoric rings. Tom Ruen (talk) 04:01, 15 November 2014 (UTC) I started the "Discrete Examples" section because of the 120-cell. I consider it a perfect example of the Hopf fibration in a different context. A "physical" example. People might not "get it" when given equations, or theory, or even a continuum picture, but seeing the 120-cell example might provide an "aha moment"! You can SEE it in the Todesco Youtube video of the 120-cell. The other face-to-face cases quickly became obvious. Then somebody mentioned, without any references, the BC helices in the 600-cell, and all the tet based polytope fibrations fell into place also. For the most part math articles have been a pretty safe subject to edit as it's objective, self documenting, except for very esoteric stuff, and people who don't know anything about it are usually uninterested, unlike articles on subjects like say, Martin Luther King, or Hitler, or date rape, where all the social justice warriors and polemicists come out to play. When Eppstein first complained about references over a year ago I did a web search. There are bits and pieces on various web sites and blogs, including some on John Baez's blog, but I could not find any coherent full coverage of the subject, which in any case is pretty obvious to interested parties. But I do know that making snide and sarcastic remarks on the rather competent and prolific work of a Wikipedia math illustrator is over the top. Cloudswrest (talk) 02:00, 17 November 2014 (UTC)
- ↑ 31.0 31.1 It is important to distinguish dimensional analogy from ordinary metaphorical analogy. Dimensional analogy[15] is a rigorous geometric process that can function as a guide to proof. Problems attacked by this method are frequently intractable when reasoning from n dimensions to more than n, but it is a scientific method because any solutions which it does yield may be readily verified (or falsified) by reasoning in the opposite direction. Cite error: Invalid
<ref>tag; name "dimensional analogy" defined multiple times with different content - ↑ A dimensional analogy is not a metaphor that we are free to adopt or replace, like the conventional names of the 4-polytopes. The 600-cell is the unique 4-dimensional analogue of the icosahedron in a precise mathematical sense. The symmetry group of the 600-cell is only sometimes called the binary icosahedral group (by metaphorical analogy), but the dimensional relationship between the 600-cell and the icosahedron which the operations of the group capture is a mathematical fact (a dimensional analogy). It is not a mistake to call the 600-cell the hexacosichoron or the 4-120-polytope or any other reasonably analogous name we may invent, but it would be a mathematical error to misidentify the 600-cell as the analogue of some other polyhedron than the icosahedron.[ae]
- ↑ As the Nobel laureate physicist I. I. Rabi famously quipped about the unanticipated muon, "Who ordered that?".
- ↑ The edges of the 600-cell form geodesic (great circle) decagons. One can pick out six orthogonal decagons, lying (for example) in the six orthogonal planes of the 4-axis coordinate system. Being completely orthogonal, these decagons share no vertices (they 'miss' each other and intersect at only one point, their common center). Thus they comprise 60 distinct vertices: half the vertices of the 600-cell. By symmetry, the other 60 vertices must occur in an exactly similar (congruent) configuration as another set of six orthogonal decagons (rotated isoclinically with respect to the first set).
- ↑ Each decagon in the orthogonal set of 6 must share two vertices (a common diameter) with each decagon to which it is not orthogonal (namely, the 66 decagons not in the set). So each set of 6 (orthogonal) decagons populates vertices in 66 (other) decagons. There are 12 sets of 6 orthogonal decagons.
- ↑ For any fixed value of 𝜂, we have a 𝜉i decagon and a 𝜉j decagon with disjoint vertex sets, because they are completely orthogonal. Conversely, the 6 decagons which intersect at each vertex cannot be mutually orthogonal, and each must have a different value of 𝜂.
- ↑ The √2.𝚽 = φ and √3.𝚽 chords produce irregular interior faces and cells, since they make isosceles great circle triangles out of two chords of their own size and one of another size.
- ↑ A golden triangle is an isosceles triangle in which the duplicated side a is in the golden ratio to the distinct side b:
- a/b = ϕ = 1 + √5/2 ≈ 1.618
The vertex angle is:- 𝛉 = arccos(ϕ/2) = 𝜋/5 = 36°
- ↑ This is another aspect of the same pentagonal symmetry which permits the partitioning of the 600-cell into icosahedral clusters of 20 cells and clusters of 5 cells.
- ↑ Clifford parallels are non-intersecting curved lines that are parallel in the sense that the perpendicular (shortest) distance between them is the same at each point. A double helix is an example of Clifford parallelism in ordinary 3-dimensional Euclidean space.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedcompletely orthogonal planes - ↑ I don't recall de Jong ever writing about 4-dimensional polytopes, but he has a large body of work experimenting with physical and virtual models of geodesics and especially tensegrity structures.
- ↑ Buckminster Fuller never quite got his mind around 4-polytopes, despite knowing Coxeter, but much of what he observed about the 3-polytopes is directly relevant to the 4-polytopes and original; he had splendid intuition. For example in his obsession with the cuboctahedron (which he called the "vector equilibrium") he was probably the first to sense the real importance of the radially equilateral polytopes. Looking at the 24-cell and tesseract makes me sad for him that he never realized the fourth dimension has a regular vector equilibrium, one of two radially equilateral regular polytopes (the other of which is the hypercube!). Just as Fuller's studies and those he inspired (such as [[1]]) are often relevant to the 4-polytopes, the 4-polytopes now inspire new 3-dimensional inventions, such as new forms of Fuller's geodesic domes[19] memes.
- ↑ In four dimensions up to 6 planes through a common point may be mutually orthogonal. The 18 great squares of the 24-cell comprise three sets of 6 orthogonal planes. The 16 great hexagons, however, comprise four sets of just 4 orthogonal planes. In four dimensions there is both a symmetrical arrangement of 6 orthogonal planes, and a symmetrical arrangement of 4 orthogonal planes. We can pick out 6 orthogonal squares in the 16-cell, 8-cell, or 24-cell, but the symmetry of 4 orthogonal hexagons emerges only in the 24-cell.
- ↑ For example:
( 0, 0, 1, 0)
( 1/2,–1/2, 1/2,–1/2) ( 1/2, 1/2, 1/2, 1/2)
(–1/2,–1/2,–1/2,–1/2) (–1/2, 1/2,–1/2, 1/2)
( 0, 0,–1, 0)
are the two opposing central triangles on the y axis (in this coordinate system of edge length √3). - ↑ ...add coordinates example to existing note...
- ↑ Each of these 96 triangular planes sections the 24-cell 1/2 edge-length below a vertex, and 1/2 edge-length above the center, measured from the center of the triangle, which is on a 24-cell diameter joining two opposite vertices. However, these paired parallel triangular planes are not orthogonal to the diameter line; they are inclined with respect to it. Each plane contains only one triangle (unlike the central hexagonal planes with their two opposing triangles), but they occur in co-centric sets of four, inclined different ways about the diameter line. The 96 triangles are inclined both with respect to the coordinate system's 6 orthogonal planes (the 6 perpendicular squares) and with respect to the hexagons. Each triangle contains one vertex from a square, and two from different hexagons. Thus their Cartesian coordinates take many different forms, but as examples:
( 0, 0, 1, 0)
( 1/2,–1/2, 1/2,–1/2) ( 1/2, 1/2, 1/2, 1/2)
(–1/2,–1/2,–1/2,–1/2) (–1/2, 1/2,–1/2, 1/2)
( 0, 0,–1, 0)
is one of the four face triangles with one vertex at the positive vertex on the y axis; and below is the opposite face of one of the two tetrahedra it is a face of, inclined about the negative part of the y axis:
( 0, 0, 1, 0)
( 1/2,–1/2, 1/2,–1/2) ( 1/2, 1/2, 1/2, 1/2)
(–1/2,–1/2,–1/2,–1/2) (–1/2, 1/2,–1/2, 1/2)
( 0, 0,–1, 0)
- ↑ The geometry of the tesseract cube volume centers is exactly the same as the vertices: a cubical vertex figure, in which four long diameters cross at the center. They are 24 interior vertices, arrayed as a 1/2 size 24-cell around the central interior vertex, at the midpoints of the 24 unit-length radii (which pass through opposite face centers of the vertex figure).
Citations
[edit | edit source]- ↑ Sadoc 2001, pp. 575-576, §2.2 The Hopf fibration of S3.
- ↑ Waegell & Aravind 2009.
- ↑ Perez-Gracia & Thomas 2017.
- ↑ 4.0 4.1 Coxeter 1973, pp. 217-218, §12.2 Congruent transformations.
- ↑ Borovik 2006, pp. 18-19, §1. Mirrors and Reflections.
- ↑ Coxeter 1938.
- ↑ Coxeter 1973, pp. 33-38, §3.1 Congruent transformations.
- ↑ Coxeter 1973, p. 38, §3.14; "Every displacement is a screw-displacement (including, in particular, a rotation or a translation)."
- ↑ Coxeter 1973, pp. 213-217, §12.1 Orthogonal transformations; "The general displacement preserving the origin in four dimensions is a double rotation.... The two completely orthogonal planes of rotation are uniquely determined except when 𝜉2 = 𝜉1, in which case... we have a Clifford displacement."
- ↑ Coxeter 1973, §12.2 Congruent transformations.
- ↑ Stillwell 2001, p. 24, Figure 7. Soap bubble 120-cell.
- ↑ Waegell & Aravind 2009, pp. 4-5, §3.4 The 24-cell: points, lines and Reye’s configuration; In the 24-cell Reye's "points" and "lines" are axes and hexagons, respectively.
- ↑ "Model of Gravitational Interaction in the Concept of Gravitons". sergf.ru. Retrieved 2019-05-11.
- ↑ http://vixra.org/pdf/1209.0110v1.pdf
- ↑ 15.0 15.1 Coxeter 1973, pp. 118-119, §7.1. Dimensional Analogy.
- ↑ van Ittersum 2020, pp. 85-86, §4.3.4 Quaternions with real part 1/2 in each 24-cell in the 600-cell 2I.
- ↑ Kim & Rote 2016, pp. 8-10, Relations to Clifford Parallelism.
- ↑ Perez-Gracia, Alba; Thomas, Federico (2016-05-14). "On Cayley’s Factorization of 4D Rotations and Applications". Advances in Applied Clifford Algebras 27 (1): 523–538. doi:10.1007/s00006-016-0683-9. ISSN 0188-7009. http://dx.doi.org/10.1007/s00006-016-0683-9.
- ↑ Miyazaki 1990; Miyazaki showed that the surface envelope of the 600-cell can be realized architecturally in our ordinary 3-dimensional space as physical buildings (geodesic domes).
- ↑ Gary Meisner (May 15, 2012). "Pi, Phi and Fibonacci": Robert Everest discovered that you can express ϕ as a function of 𝜋 and the numbers 1, 2, 3 and 5 of the Fibonacci series: ϕ = 1 – 2 cos (3𝜋/5)
{{cite web}}: CS1 maint: postscript (link) - ↑ http://eusebeia.dyndns.org/4d/rect24cell
References
[edit | edit source]- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. 6. University of Toronto Studies (Mathematical Series).
- Borovik, Alexandre (2006). "Coxeter Theory: The Cognitive Aspects". In Davis, Chandler; Ellers, Erich. The Coxeter Legacy. Providence, Rhode Island: American Mathematical Society. ISBN 978-0821837221. https://www.academia.edu/26091464/Coxeter_Theory_The_Cognitive_Aspects.
- Miyazaki, Koji (1990). "Primary Hypergeodesic Polytopes". International Journal of Space Structures 5 (3–4): 309–323. doi:10.1177/026635119000500312.
- Nishio, Kengo; Miyazaki, Takehide (2018). "Polyhedron and Polychoron Codes for Describing Atomic Arrangements". In Tanaka. Nanoinformatics. Singapore: Springer. pp. 97-130. https://link.springer.com/chapter/10.1007/978-981-10-7617-6_6.
- Waegell, Mordecai; Aravind, P. K. (2009-11-12). Critical noncolorings of the 600-cell proving the Bell-Kochen-Specker theorem (in en). doi:10.1088/1751-8113/43/10/105304. https://arxiv.org/abs/0911.2289v2.
- Sadoc, Jean-Francois (2001). "Helices and helix packings derived from the {3,3,5} polytope". European Physical Journal E 5: 575–582. doi:10.1007/s101890170040. https://www.researchgate.net/publication/260046074.