Zenbakizko integrazio

Zenbakizko integrazioa Monte Carlo metodoa erabiliz: Nodoak ausaz banatzen dira integrazio tartean. Puntu berriak urdin ilunez irudikatzen dira, eta puntu zaharrak urdin argiz. Integralaren balio zehatza 3,32 da

Zenbakizko analisian, zenbakizko integrazioa algoritmo sorta zabal bat da integral definitu baten zenbakizko balioa kalkulatzeko, Hedaduraz, batzuetan ekuazio diferentzialak ebazteko zenbakizko algoritmoak deskribatzeko ere erabiltzen da. Artikulu hau integral mugatuen zenbakizko kalkuluari buruzkoa da.

Zenbakizko integrazioko formulak koadratura formula bezala ere ezagutzen dira, batez ere dimentsio bakarreko integralen kasuan. Bi dimentsio edo gehiagoko integralak (integral anizkoitzak) kalkulatzeko zenbakizko formulei kubatura formula esaten zaie batzuetan, nahiz eta kasu horietan koadratura terminoa ere erabiltzen den.

Zenbakizko integrazioaren xedea

$\int _{a}^{b}f(x)\,dx$

moduko integral mugatuak modu hurbilduan (doitasun maila jakin batekin) kalkulatzea da.

Zenbakizko integraziorako motibazioa

Integral mugatuak Barrow-ren erregelaren bidez kalkula daitezke zehazki, integratu nahi den funtzioaren antideribatua (jatorrizko funtzioa) aurkitzen gai izanez gero. Antideribatua erraz baliozta daitekeen funtzio elementala denean, zenbakizko integrazioko metodoek ez dute zentzu handirik. Zenbakizko integrazioko teknikak erabiltzea egokia izan daitezke hainbat kasuetan:

1. Integratu nahi den $f(x)$ funtzioaren (integrakizunaren) balioa zenbait puntuetan ezagutzen bada soilik.
2. Jatorrizko funtzioa eragiketa eta funtzio elementalen arabera adierazi ezin denean.
3. Jatorrizko funtzioa balioztatzea konputazionalki garestia denean.

Kasu horietan, integral mugatua integrakizunaren hainbat puntuetako balioen konbinazio lineal gisa hurbil daiteke. Horrela lortutako balioa ez da zehazki integral mugatua izango, errorea egingo dugu. Errore hori oro har zero izango ez den arren, nahi bezain txikia egin daiteke, integrakizunaren behar adina balioztapen eginez gero.

Historia

"Zenbakizko integrazio" terminoa 1915ean agertzen da lehen aldiz David Gibben A Course in Interpolation and Numeric Integration for the Mathematics Laboratory argitalpenean.

Koadratura termino matematiko historikoa da, eremua kalkulatzea esan nahi duena. Koadratura problemak analisi matematikoaren iturri nagusietako bat izan dira. Antzinako Greziako matematikariek, pitagorikoen doktrinaren arabera, azaleraren kalkulua geometrikoki karratu bat eraikitzeko prozesu gisa ulertu zuten, eremu bera duena (karratua). Horregatik jarri zioten koadratura izena prozesuari. Adibidez, zirkuluaren koadratura, Hipokrates Txioskoaren lunula, Parabolaren koadratura. Eraikuntza hori konpas eta erregela bidez bakarrik egin behar da.

Antzinako babiloniarrek, arau trapezoidala, Jupiterren mugimendua ekliptikan integratzeko erabili zuten.

Metodo zaharra batezbesteko geometrikoa aurkitzeko

a eta b aldedun laukizuzen baten koadraturako, albodun lauki bat eraiki behar da.

$x={\sqrt {ab}}$ (a eta b-ren batezbesteko geometrikoa). Horretarako, honako egitate hau erabil daiteke: zirkulua diametro gisa a eta b batuz marrazten badugu, orduan BH altuera (zirkulu batekin gurutzatzeko duten loturaren puntu batetik) bere batezbesteko geometrikoaren parekoa da. Antzeko eraikuntza geometrikoak lauki baten problema konpontzen du paralelogramo eta triangelu batentzat.

Parabola baten zati baten eremua.

Koadratura arazoak irudi bihurrientzat askoz ere zailagoak dira. XIX. mendean, konpasarekin eta erregelarekin ezinezkoa zela zirkuluaren koadratura lortu frogatu zen. Hala ere, irudi batzuentzat (adibidez, Hipokrates Txioskoaren lunula) koadratura bat egin daiteke. Arkimedesek egindako esfera-azaleraren eta parabola segmentuaren koadratuak antzinako analisiaren lorpenik handiena bihurtu ziren.

• Esfera baten azalera esfera horren zirkulu handi baten azalera laukoiztearen parekoa da.
• Lerro zuzen batez ebakitako parabolaren segmentu baten eremua segmentu horretan inskribatutako triangeluaren azaleraren 4/3 da.

Emaitzak frogatzeko, Arkimedesek Eudoxoren exhauzio-metodoa erabili zuen.

Erdi Aroko Europan, koadraturak azaleraren kalkulua esan nahi zuen, edozein metodo erabiliz. Maizago, zatiezinen metodoa erabili zen ; ez zen hain zorrotza, baina bai sinpleagoa eta ahaltsuagoa. Galileo Galileik eta Gilles de Robervalek arku zikloide baten eremua aurkitu zuten, Grégoire de Saint-Vincentek hiperbola batenpean zegoen eremua ikertu zuen (Opus Geometricum, 1647), eta Alphonse Antonio de Sarasak, Saint-Vincenteren ikasle eta iruzkingileak, gune horrek logaritmoekin zuen harremana egiaztatu zuen.

John Wallisek metodo hau algebrara ekarri zuen: bere Arithmetica infinitorum (1656) lanean orain integral zehaztua deitzen diogun seriea idatzi zuen, eta haien balioak kalkulatu zituen. Isaac Barrowek eta James Gregory-k aurrera jo zuten: kurba aljebraiko eta kiribil batzuetarako koadratuak. Christiaan Huygensek arrakastaz egin zuen biraketa-solido batzuen kuadratura.

Saint-Vincent eta Sarasaren hiperbolaren koadraturak funtzio berri bat ekarri zuen, logaritmo naturala, garrantzi kritikoa izan zuena.

Kalkulu integralaren asmakuntzarekin azalerak kalkulatzeko metodo unibertsal bat sortu zen. Horri erantzunez, koadratura terminoa tradizional bihurtu da, eta, horren ordez, arruntagoa da esaldi modernoa: Integral determinatu eta unibokoaren zenbaketa.

Dimentsio bakarreko integraletarako metodoak

Aldagai bakarreko funtzioen integral mugatuak modu hurbilduan kalkulatzeko zenbakizko integrazioko metodo bat zehazteko, integrakizuna zein puntutan balioztatuko den jakin behar da (hau da, integrazio puntuak zein diren) eta zein diren funtzioaren balioen zein konbinazio lineale egingo den esaten duten integrazio pixuak.

Zenbakizko edozein integrazio-metodoren analisiaren zati garrantzitsu bat hurbilketa-errorearen portaera aztertzea da. Integrakizunaren balioztapen kopuru txikiarekin errore txikia lortzen duten metodo edo koadratura formulak hobetsiko dira.

Integratu behar den funtzioaren ebaluazio kopurua murrizteak eragiketa aritmetikoen kopurua murrizten du. Horrek kalkulu-denbora murrizten du. Kalkuluak koma flotatzaileko eragiketen bidez egiten direnean (gehienak), eragiketa kopurua murrizteak biribiltze osoaren errorea ere murrizten du.

Interpolazio-funtzioetan oinarritutako metodoak

Integratu beharreko $f(x)$ funtzioa integral zehatza ezagutzen den $g(x)$ beste funtzio baten bidez hurbiltzean oinarritzen den metodo-familia zabal bat badago. Jatorrizkoa ordezten duen funtzioa puntu kopuru jakin batean jatorrizkoaren balio bera izateko moduan bilatu behar da. Muturreko puntuak beti puntu-multzo horren parte direnez, funtzio berriari jatorrizko funtzioaren interpolazio deritzo. Muturreko puntuak jatorrizkoaren ordezko funtzioa aurkitzeko erabiltzen ez direnean, estrapolazioa esaten zaio. Funtzio horiek polinomioak izan ohi dira.

Newton-Cotesen formulak

Polinomioekiko interpolazioa$\ [a,b]$ tartean honogeneoki bereizitako puntuetan ebaluatuz Newton-Cotesen formulak sortzen dira, zeinen adibide baitira laukizuzenaren araua, trapezioarena eta Simpsonena. Nodoak tartearen muturrak barne $k=n+1$ hartu arte aukeratzen badira, Newton-Cotesen formula itxia izango da, eta $k=n-1$ nodo hautatzen badira edo muturrak ez badituzte hartzen tabulatutako datuek Newton-Cotes irekiaren formula izango da.

Laukizuzenaren erregela

Mota honetako metodorik sinpleena da funtzio interpolatzailea funtzio konstante bat izatea (zero ordenako polinomio bat), puntutik pasatzen dena.$(a,f(a))$ Metodo horri laukizuzenaren erregela deritzo:

$\int _{a}^{b}f(x)dx\sim (b-a)f(a)$

Erdiko puntuaren araua

Erdiko puntuko arauaren irudia.

Aurreko metodoan funtzioa $\left({\frac {a+b}{2}},f\left({\frac {a+b}{2}}\right)\right)$puntutik pasatzen bada, metodo horri erdiko puntuaren araua esaten zaio:

$\int _{a}^{b}f(x)dx\sim (b-a)\,f\!\left({\frac {a+b}{2}}\right)$

Trapezioaren erregela

Erdiko puntuko arauaren irudia.

Jatorrizko ekuazioaren ordezko polinomioa lehen mailakoa den kasuari dagokio, nahiz eta jatorrizko formula $\left({\frac {a+b}{2}},f\left({\frac {a+b}{2}}\right)\right)$puntutik igaro ez. Orduan, bai:

$I=\int _{a}^{b}\left[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)\right]dx$

integrazio-araua da:

$I=(b-a){\frac {f(a)+f(b)}{2}}$

erdiko puntuaren erregelan erabilitako formula bera dena.

Simpson-en araua

Simpsondarren arauaren irudia.

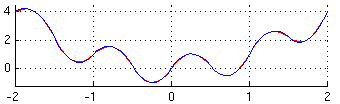
Interpolazio-funtzioa 2. mailako polinomio bat izan daiteke, eta $\ (a,f(a))$, $({\frac {a+b}{2}},f({\frac {a+b}{2}}))$ eta $\ (b,f(b))$ puntuetatik igarotzen dena. Metodo horri Simpson-en erregela deritzo:

.$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right]$

Arau konposatuak

Edozein arau interpolatzailetarako, hurbilketa zehatzagoa egin daiteke $\ [a,b]$ tartea $\ n$ kopuru azpizatitan zatituz, azpizati bakoitzerako hurbilketa bat aurkituz eta, azkenik, emaitza guztiak batuz. Hori eginez sortzen diren arauei arau konposatuak esaten zaie, eta haien ezaugarria da doitasun orokorreko ordena bat galtzen dutela dagozkien arau sinpleen aldean, nahiz eta, oro har, integralaren balio zehatzagoak ematen dituzten, metodoaren kostu operatiboa nabarmen handitzearen kontura. Adibidez, trapezio konposatuaren araua honela adieraz daiteke:

$\int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left({\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right)$

non azpitarteek$\ [kh,(k+1)h]$ forma baitute h eta k hauek izanik:$\ h={\frac {b-a}{n}}$$\ k=0,1,2,\ldots ,n-1$

Estrapolazio-metodoak

Newton-Cotes motako integrazio-metodo baten zehaztasuna, eskuarki, ebaluazio-puntuen kopuruaren funtzio bat da. Emaitza zehatzagoa izan ohi da ebaluazio-puntuen kopurua handitzen denean, edo, bestela, puntuen arteko pasabidearen zabalera murrizten denean. Zer gertatzen da pasabidearen zabalerak zerorantz jotzen duenean? Bi zabaleraren edo gehiagoren emaitza estrapolatuz erantzun daiteke hori (Richardson-en estrapolazioa). Estrapolazio-funtzioa polinomio bat edo funtzio arrazional bat izan daiteke. Estrapolazio-metodoak zehatzago deskribatzen dituzte Stoer eta Bulirsch-ek (3.4 atala). Zehazki, trapezio konposatuaren erregelari Richardson-en estrapolazio-metodoa aplikatzean, Romberg-en metodoa lortzen da.

Gaussen koadratura

Interpolazio-puntuen arteko tarteak aldatzea onartzen bada, beste integrazio-formula multzo bat dago, Gaussen koadratura-formula deritzenak. Gaussen koadratura-arau bat zehatzagoa da integratzailearen ebaluazio-kopuru bera eskatzen duen Newton-Cotesen arau bat baino, integratzailea leuna bada (hau da, askotan erator badaiteke).

Egokitze-algoritmoak

f -k bere puntu guztietan deribatu asko definituta ez baditu, edo deribatuek oso balio handiak hartzen badituzte, gausiar integrazioa askotan ez da nahikoa. Kasu horretan, honen antzeko algoritmo batek hobeto egingo luke:

def integral(f, a, b):
    """Este algoritmo calcula la integral definida de una función
    en el intervalo [a,b], adaptativamente, eligiendo pasos más
    pequeños cerca de los puntos problemáticos.
    h0 es el paso inicial."""
    
    x = a
    h = h0
    acumulador = 0
    while x < b:
        if x+h > b:  h = b - x
        if error de la cuadratura sobre [x,x+h] para f es demasiado grande:
            haz h más pequeño
        else:
            acumulador += integral(f, x, x+h)
            x += h
            if error de la cuadratura sobre [x,x+h] es demasiado pequeño:
                haz h más grande
    return acumulador

Algoritmoaren xehetasun batzuk arretaz aztertu behar dira. Kasu askotan, f funtzio baterako tarte batean integralak duen errorea zenbatestea ez da begi-bistakoa. Ohiko irtenbide bat bi integrazio-arau desberdin erabiltzea da, eta haien arteko aldea integralaren akatsaren zenbatespen gisa hartzea. Beste arazoa zer den «handiegia» edo «txikiegia» erabakitzea da. Integralaren errorea th baino handiagoa ez izatea izan daiteke «handiegia»rentzako irizpide posible bat, non t zenbaki erreal bat baita errore orokorrarentzat izan nahi dugun tolerantzia. Baina, gainera, h txikia bada, are txikiagoa egiteak ez du merezi, integralaren errorea itxuraz handia bada. Errore-analisi mota horri «a posteriori» deritzo, hurbilketa kalkulatu ondoren kalkulatzen baitugu errorea.

Egokitze-integraziorako heuristika eztabaidatua dago Forsythe et al (5.4 atala) lanean.

Errore kontserbatzailearen zenbatespena (a priori)

Demagun $\ f$ funtzioak lehenengo deribatu bat duela $\ [a,b]$ tarte kotatuaren gainean. Hau da batez besteko balioaren teoremak$\ f$ funtziorako $\ x<b$ denean

$\ (x-a)f'(y_{x})=f(x)-f(a)$

$\ [a,x]$ tarteko $\ y_{x}$ baten baterako,$\ x$-ren arabera.Berdintasunaren bi aldeetan $\ x$-ren arabera $\ a$-tik $\ b$-raino integratzen badugu eta balio absolutuak hartzen baditugu, honako hau lortzen dugu:

$\left|\int _{a}^{b}f(x)dx-(b-a)f(a)\right|=\left|\int _{a}^{b}(x-a)f'(y_{x})dx\right|$

Integralaren hurbilketa handiagoa egin daiteke eskuinaldean, integratuan balio absolutua sartuz eta terminoaren ordez goragoko kota bat jarriz:$\ f$

$\left|\int _{a}^{b}f(x)dx-(b-a)f(a)\right|\leq {\frac {(b-a)^{2}}{2}}\sup _{a\leq x\leq b}\left|f'(x)\right|$

Hala, $\int _{a}^{b}f(x)dx$ integrala $\ (b-a)f(a)$ integrazio-erregelaren bidez hurbiltzen badugu, hurbiltze-errorea ez da ekuazioaren eskuineko aldea baino handiagoa.

Integral anizkunak

Orain arte aipatu diren integrazio-metodoak dimentsio baten integralak kalkulatzeko diseinatu dira guztiak.

Hainbat dimentsiotako integralak kalkulatzeko, ikuspegi bat da integral anizkoitza dimentsio baten integralen errepikapen gisa adieraztea, Fubiniren teorema erabiliz.

Ikuspegi horrek funtzioaren ebaluazio kopuru bat dakar, eta esponentzialki handitzen da dimentsio-kopurua handitu ahala. Bi metodo ezagutzen dira dimentsioaren madarikazio hori gainditzeko.

Montecarlo

Montecarloko metodoak eta kuasi-Montecarloko metodoak erraz aplika dakizkieke integral multidimentsionalei, eta zehaztasun hobea lortu dezakete, funtzioaren ebaluazio kopuru berarekin, errepikatutako integrazioak eginez baino, dimentsio bakarreko metodoak erabiliz. Montecarloko metodo erabilgarri mota handi bat Montecarloko Markov kateko algoritmoak dira, esaterako, Metropolis-Hastingseko algoritmoa eta Gibbsen laginketa .

Parrilla sakabanatuak

Hasieran, Smolyak-ek garatu zituen parrilla sakabanatuak, hainbat dimentsiotako funtzioen koadraturarako. Metodo hori dimentsio bakarreko koadratura-metodo batean oinarritzen da beti, baina aldagai bakoitzaren emaitzen konbinazio sofistikatuagoa egiten du.

Ekuazio diferentzialekiko lotura

Integral hau ebaluatzeko arazoa

$\int _{a}^{b}f(x)\,dx$

ekuazio diferentzial arrunt baten hasierako balioaren problema batera murritz daiteke. Goiko integrala I(b) gisa idazten bada, I funtzioak hau betetzen du:

$I'(x)=f(x),\quad I(a)=0.$

Ekuazio diferentzial arruntak ebazteko garatutako metodoak, hala nola Runge-Kutta metodoak, problema ebazteko erabil daitezke, eta, beraz, integrala ebaluatzeko erabil daitezke.

Zenbakizko integraziorako programak

Zenbakizko integrazioa da zenbakizko analisian gehien aztertu den arazoetako bat. Programa horien inplementazio ugarien artean hauek daude:

• QUADPACK (SLATECen zatia) (iturburu-kodea): QUADPACK Fortran algoritmo-bilduma bat da, arau gausiarretan oinarritutako zenbakizko integraziorako.
• GSL: GNU Scientific Library. GNUko Liburutegi Zientifikoa (GSL) C-n idatzitako zenbakizko-liburutegia da, eta errutina matematiko ugari ematen ditu, hala nola Montecarloko integrazioa.
• ALGLIB: Zenbakizko integraziorako algoritmo-bilduma bat da C# / C++ / Delphi / Visual Basic / etc.-en.

Zenbakizko integrazioko algoritmoak aurki daitezke GAMS class H2-n.

Bibliografia

• Philip J. Davis eta Philip Rabinowitz, Methods of Numerical Integration.
• George E. Forsythe, Michael A. Malcolm, eta Cleve B. Moler. Konputer Methods for Mathematical Computations. Englewood Cliffs, NJ: PrenticeHall, 1977. (Ikus 5. kapitulua.)
• William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling. Numerical Recipes in C. Cambridge, Erresuma Batua: Cambridge University Press, 1988. (Ikus 4. kapitulua.)
• Josef Stoer and Roland Bulirsch. Zenbakizko analisia sartzea. New York: Springer-Verlag, 1980. (Ikus 3. kapitulua.)
• Jon M. Smith Recent Developments in Numerical Integration, J. Dynam. Sys., Measurement and Control 96, Ser. G-1, Ez. 1, 61-70, Mar. 1974.

Kanpo estekak

Wikimedia Commonsen badira fitxategi gehiago, gai hau dutenak: Zenbakizko integrazio

• Zurruntasun-Indar metodoaren inplementazioa konpositeen saiakuntza mekanikoetan. Nagore Insausti Irastorza. Donostia., 2019ko apirilean
• «Mathematica» Angulo, Patxi eta Elena Lazkano. Zientzia.eus (1998-04-01)
• Integración: Antecedentes, Simulaciones, etc. en el Holistic Numerical Methods Institute
  • Datuak: Q753445
  • Multimedia: Numerical integration / Q753445