Un article de Wikipédia, l'encyclopédie libre.
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. En théorie des probabilités , une loi triangulaire est une loi de probabilité dont la fonction de densité est affine de sa borne inférieure à son mode, et de son mode à sa borne supérieure.
Elle est mentionnée sous deux versions : une loi discrète et une loi continue.
La loi triangulaire discrète de paramètre entier positif a est définie pour tout entier x compris entre –a et a par :
P
(
x
)
=
a
+
1
−
|
x
|
(
a
+
1
)
2
{\displaystyle \mathrm {P} (x)={\frac {a+1-|x|}{(a+1)^{2}}}}
Triangulaire
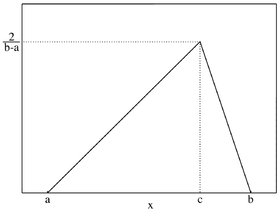
Densité de probabilité Densité de la loi triangulaire
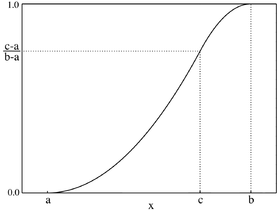
Fonction de répartition Fonction de répartition de la loi triangulaire
Paramètres
a
:
a
∈
(
−
∞
,
∞
)
{\displaystyle a:~a\in (-\infty ,\infty )}
b
:
b
>
a
{\displaystyle b:~b>a\,}
c
:
a
≤
c
≤
b
{\displaystyle c:~a\leq c\leq b\,}
Support
a
≤
x
≤
b
{\displaystyle a\leq x\leq b\!}
Densité de probabilité
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
pour
a
<
x
≤
c
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
pour
c
<
x
≤
b
{\displaystyle \left\{{\begin{matrix}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{pour }}a<x\leq c\\{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{pour }}c<x\leq b\end{matrix}}\right.}
Fonction de répartition
{
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
pour
a
<
x
<
c
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
pour
c
<
x
≤
b
{\displaystyle \left\{{\begin{matrix}{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{pour }}a<x<c\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{pour }}c<x\leq b\end{matrix}}\right.}
Espérance
a
+
b
+
c
3
{\displaystyle {\frac {a+b+c}{3}}}
Médiane
{
a
+
(
b
−
a
)
(
c
−
a
)
2
pour
c
≥
b
−
a
2
b
−
(
b
−
a
)
(
b
−
c
)
2
pour
c
≤
b
−
a
2
{\displaystyle \left\{{\begin{matrix}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{pour }}c\!\geq \!{\frac {b\!-\!a}{2}}\\&\\b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{pour }}c\!\leq \!{\frac {b\!-\!a}{2}}\end{matrix}}\right.}
Mode
c
{\displaystyle c\,}
Variance
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
{\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
Asymétrie
2
(
a
+
b
−
2
c
)
(
2
a
−
b
−
c
)
(
a
−
2
b
+
c
)
5
(
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
)
3
2
{\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
Kurtosis normalisé
−
3
5
{\displaystyle -{\frac {3}{5}}}
Entropie
1
2
+
ln
(
b
−
a
2
)
{\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
Fonction génératrice des moments
2
(
b
−
c
)
e
a
t
−
(
b
−
a
)
e
c
t
+
(
c
−
a
)
e
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle 2{\frac {(b\!-\!c){\rm {e}}^{at}\!-\!(b\!-\!a){\rm {e}}^{ct}\!+\!(c\!-\!a){\rm {e}}^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
Fonction caractéristique
−
2
(
b
−
c
)
e
i
a
t
−
(
b
−
a
)
e
i
c
t
+
(
c
−
a
)
e
i
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle -2{\frac {(b\!-\!c){\rm {e}}^{{\rm {i}}at}\!-\!(b\!-\!a){\rm {e}}^{{\rm {i}}ct}\!+\!(c\!-\!a){\rm {e}}^{{\rm {i}}bt}}{(b-a)(c-a)(b-c)t^{2}}}}
modifier
La loi triangulaire continue sur le support ]a ; b [ et de mode c a pour fonction de densité :
f
:
x
↦
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
si
a
<
x
≤
c
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
si
c
<
x
≤
b
0
sinon
{\displaystyle f\colon x\mapsto {\begin{cases}\displaystyle {\frac {2(x-a)}{(b-a)(c-a)}}&{\text{ si }}a<x\leq c\\\\\displaystyle {\frac {2(b-x)}{(b-a)(b-c)}}&{\mbox{ si }}c<x\leq b\\\\0&{\text{ sinon}}\end{cases}}}
Dans de nombreux domaines, la loi triangulaire est considérée comme une version simplifiée de la loi bêta .
Soit X1 et X2 deux variables indépendantes et identiquement distribuées selon une loi uniforme standard . Alors:
la distribution de la moyenne
Y
:=
X
1
+
X
2
2
{\displaystyle \mathrm {Y} :={\frac {\mathrm {X} _{1}+\mathrm {X} _{2}}{2}}}
est une loi triangulaire de paramètres a = 0, b = 1 et c = ½. C'est alors un cas particulier de la loi Bates , avec n = 2. la distribution de l'écart absolu
Z
:=
|
X
1
−
X
2
|
{\displaystyle \mathrm {Z} :=|\mathrm {X} _{1}-\mathrm {X} _{2}|}
est aussi distribué selon une loi triangulaire de paramètres a = 0, b = 1 et c = 0. (en) Eric W. Weisstein , « Triangular Distribution MathWorld