התפלגות לפלס

התפלגות לפלס

פונקציית ההסתברות
px
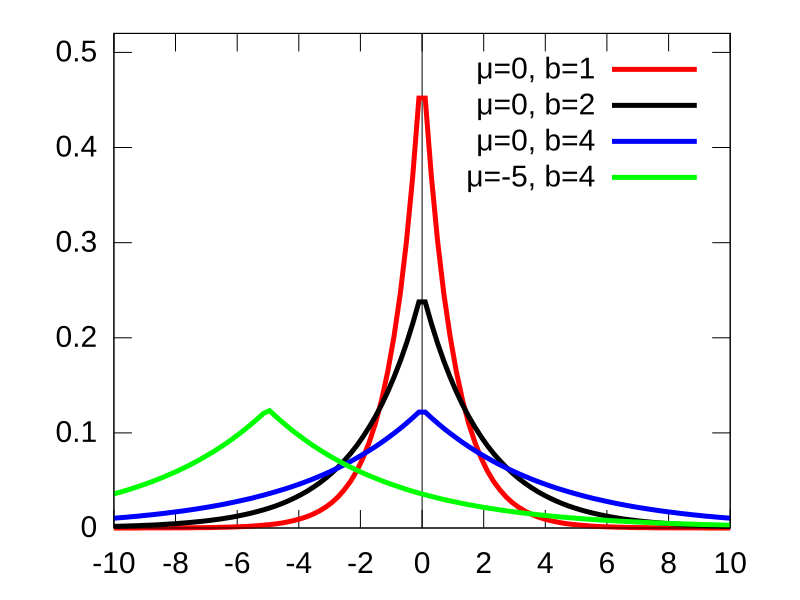
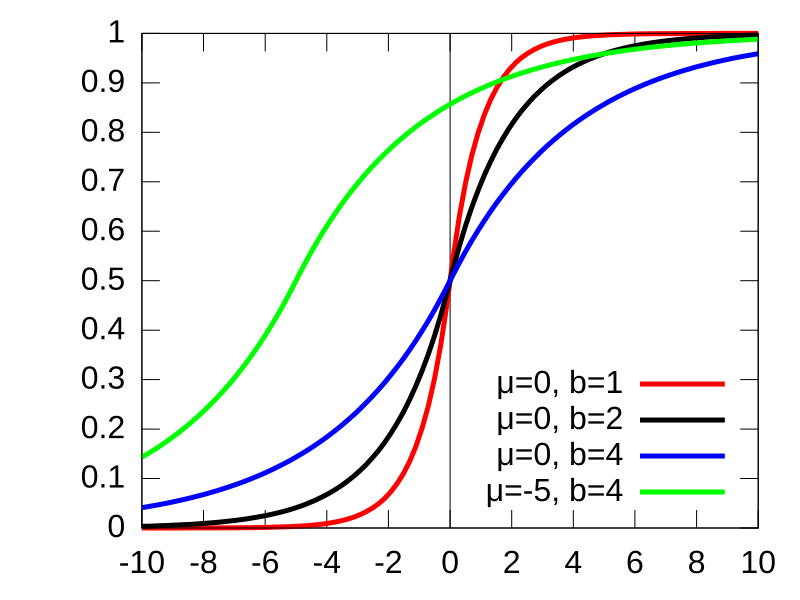
פונקציית ההסתברות המצטברת
px
מאפיינים
פרמטרים	$\mu$ (ממשי) $b>0$ (ממשי)
תומך	$\mathbb {R}$
פונקציית צפיפות הסתברות (pdf)	${\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)$
פונקציית ההסתברות המצטברת (cdf)	${\begin{cases}{\frac {1}{2}}\exp \left({\frac {x-\mu }{b}}\right)&{\text{if }}x\leq \mu \\[8pt]1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\text{if }}x\geq \mu \end{cases}}$
תוחלת	$\mu$
חציון	$\mu$
ערך שכיח	$\mu$
שונות	$2b^{2}$
אנטרופיה	$\log(2be)$
פונקציה יוצרת מומנטים (mgf)	${\frac {\exp(\mu t)}{1-b^{2}t^{2}}}{\text{ for }}|t|<1/b$
פונקציה אופיינית	${\frac {\exp(\mu it)}{1+b^{2}t^{2}}}$
צידוד	$0$
גבנוניות	$3$

בתורת ההסתברות ובסטטיסטיקה, התפלגות לפלס היא התפלגות הסתברות רציפה הקרויה על שם פייר-סימון לפלס. היא נקראת לפעמים גם התפלגות מעריכית כפולה, כיוון שניתן לראותה כשתי התפלגויות מעריכיות (עם פרמטר מיקום נוסף) המחוברות יחדיו, אם כי המונח משמש לעיתים גם להתייחסות להתפלגות גומבל.

הגדרות

פונקציית צפיפות הסתברות

פונקציית צפיפות ההסתברות של התפלגות לפלס עם פרמטרים $\mu$ ו $b$ היא

$f(x\mid \mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right),$ .

$\mu$ הוא פרמטר מיקום, ו $b>0$ הוא פרמטר קנה מידה. אִם $\mu =0$ ו $b=1$, ההתפלגות על חצי הישר הממשי זהה להתפלגות המעריכית עד כדי פקטור 1/2.

פונקציית צפיפות ההסתברות של התפלגות לפלס דומה לזו של ההתפלגות הנורמלית; עם זאת, בעוד שההתפלגות הנורמלית מתבטאת במונחים של ריבוע ההפרש מהממוצע $\mu$, צפיפות לפלס מתבטאת במונחי הערך המוחלט של ההפרש מהממוצע. כתוצאה מכך, להתפלגות לפלס יש זנב עבה יותר מזה של ההתפלגות הנורמלית. זהו מקרה פרטי של ההתפלגות הנורמלית המוכללת וההתפלגות ההיפרבולית. התפלגויות סימטריות רציפות שיש להן זנבות אקספוננציאליים, כמו התפלגות לפלס, אך בעלות פונקציות צפיפות הסתברות בעלות נגזרת רציפה גם בשכיח כוללות את ההתפלגות הלוגיסטית והתפלגות הסקנט ההיפרבולי.

פונקציית התפלגות מצטברת

קל לבצע אינטגרציה של פונקציית הצפיפות של התפלגות לפלס, לקבל את פונקציית ההתפלגות המצטברת:

${\begin{aligned}F(x)&=\int _{-\infty }^{x}\!\!f(u)\,\mathrm {d} u={\begin{cases}{\frac {1}{2}}\exp \left({\frac {x-\mu }{b}}\right)&{\mbox{if }}x<\mu \\1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{if }}x\geq \mu \end{cases}}\\&={\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {sgn}(x-\mu )\left(1-\exp \left(-{\frac {|x-\mu |}{b}}\right)\right).\end{aligned}}$

הפונקציה ההופכית להתפלגות המצטברת היא

$F^{-1}(p)=\mu -b\,\operatorname {sgn}(p-0.5)\,\ln(1-2|p-0.5|)$ .

תכונות

מומנטים

$\mu _{r}'={\bigg (}{\frac {1}{2}}{\bigg )}\sum _{k=0}^{r}{\bigg [}{\frac {r!}{(r-k)!}}b^{k}\mu ^{(r-k)}\{1+(-1)^{k}\}{\bigg ]}$

התפלגויות קשורות

• אם $X\sim {\textrm {Laplace}}(\mu ,b)$ אז $kX+c\sim {\textrm {Laplace}}(k\mu +c,|k|b)$.
• אם $X\sim {\textrm {Laplace}}(0,1)$ אז $bX\sim {\textrm {Laplace}}(0,b)$.
• אם $X\sim {\textrm {Laplace}}(0,b)$ אז $\left|X\right|\sim {\textrm {Exponential}}\left(b^{-1}\right)$ (התפלגות מעריכית).
• אם $X,Y\sim {\textrm {Exponential}}(\lambda )$ אז $X-Y\sim {\textrm {Laplace}}\left(0,\lambda ^{-1}\right)$．
• אם $X\sim {\textrm {Laplace}}(\mu ,b)$ אז $\left|X-\mu \right|\sim {\textrm {Exponential}}(b^{-1})$.
• אם $X\sim {\textrm {Laplace}}(\mu ,b)$ אז $X\sim {\textrm {GND}}(\mu ,b,1)$ (התפלגות נורמלית מוכללת).
• אם $X_{1},...,X_{4}\sim {\textrm {N}}(0,1)$ (התפלגות נורמלית) אז $X_{1}X_{2}-X_{3}X_{4}\sim {\textrm {Laplace}}(0,1)$ and $(X_{1}^{2}-X_{2}^{2}+X_{3}^{2}-X_{4}^{2})/2\sim {\textrm {Laplace}}(0,1)$.
• אם $X_{i}\sim {\textrm {Laplace}}(\mu ,b)$ אז ${\frac {\displaystyle 2}{b}}\sum _{i=1}^{n}|X_{i}-\mu |\sim \chi ^{2}(2n)$ (התפלגות כי בריבוע).
• אם $X,Y\sim {\textrm {Laplace}}(\mu ,b)$ אז ${\tfrac {|X-\mu |}{|Y-\mu |}}\sim \operatorname {F} (2,2)$. (התפלגות F)
• אם $X,Y\sim {\textrm {U}}(0,1)$ (התפלגות אחידה רציפה) אז $\log(X/Y)\sim {\textrm {Laplace}}(0,1)$.
• אם $X\sim {\textrm {Exponential}}(\lambda )$ ו- $Y\sim {\textrm {Bernoulli}}(0.5)$ (התפלגות ברנולי) בלתי תלוי ב- $X$, אז $X(2Y-1)\sim {\textrm {Laplace}}\left(0,\lambda ^{-1}\right)$.
• אם $X\sim {\textrm {Exponential}}(\lambda )$ ו- $Y\sim {\textrm {Exponential}}(\nu )$ בלתי תלוי ב- $X$, אז $\lambda X-\nu Y\sim {\textrm {Laplace}}(0,1)$．
• אם $X$ מתפלג ראדמאכר ו $Y\sim {\textrm {Exponential}}(\lambda )$ אז $XY\sim {\textrm {Laplace}}(0,1/\lambda )$.

ההסתברות שמשתנה מקרי המתפלג לפלס גדול ממשתנה מקרי המתפלג לפלס

יהיו $X,Y$ משתנים מקריים בלתי תלויים המתפלגים לפלס: $X\sim {\textrm {Laplace}}(\mu _{X},b_{X})$ ו- $Y\sim {\textrm {Laplace}}(\mu _{Y},b_{Y})$. נרצה לחשב את ההסתברות $P(X>Y)$.

ניתן לפשט את $P(X>Y)$ באמצעות התכונות לעיל ל $P(\mu +bZ_{1}>Z_{2})$, כאשר $Z_{1},Z_{2}\sim {\textrm {Laplace}}(0,1)$, $\mu ={\frac {\mu _{X}-\mu _{Y}}{b_{Y}}}$ ו $b={\frac {b_{X}}{b_{Y}}}$. הסתברות זו שווה ל- $P(\mu +bZ_{1}>Z_{2})={\begin{cases}{\frac {b^{2}e^{\mu /b}-e^{\mu }}{2(b^{2}-1)}},&{\text{when }}\mu <0\\1-{\frac {b^{2}e^{-\mu /b}-e^{-\mu }}{2(b^{2}-1)}},&{\text{when }}\mu >0\\\end{cases}}$

כאשר $b=1$ ניתן להמיר את שני הביטויים בגבול שלהם כאשר $b\to 1$:

$P(\mu +Z_{1}>Z_{2})={\begin{cases}e^{\mu }{\frac {(2-\mu )}{4}},&{\text{when }}\mu <0\\1-e^{-\mu }{\frac {(2+\mu )}{4}},&{\text{when }}\mu >0\\\end{cases}}$

כדי לחשב את המקרה $\mu >0$ נשים לב כי $P(\mu +Z_{1}>Z_{2})=1-P(\mu +Z_{1}<Z_{2})=1-P(-\mu -Z_{1}>-Z_{2})=1-P(-\mu +Z_{1}>Z_{2})$

כיוון ש $Z\sim -Z$ כאשר $Z\sim {\textrm {Laplace}}(0,1)$ .

הקשר להתפלגות המעריכית

ניתן לייצג משתנה מקרי המתפלג לפלס כהפרש של שני משתנים מקריים בלתי תלויים ושווי התפלגות (iid) המתפלגים מעריכית. אחת הדרכים להראות זאת היא באמצעות גישת הפונקציה האופיינית. לכל קבוצה של משתנים מקריים רציפים בלתי תלויים, לכל שילוב ליניארי של אותם משתנים, ניתן לרכוש את הפונקציה האופיינית שלו (שקובעת באופן ייחודי את ההתפלגות) על ידי הכפלת הפונקציות האופייניות המתאימות.

הסקה סטטיסטית

בהינתן $n$ דגימות בלתי תלויות ושוות התפלגות $x_{1},x_{2},...,x_{n}$, אומד הנראות המקסימלית (MLE) של $\mu$ הוא חציון המדגם

${\hat {\mu }}=\mathrm {median} (x)$ .

אומד ה-MLE של $b$ הוא הסטייה המוחלטת הממוצעת מהחציון

${\hat {b}}={\frac {1}{n}}\sum _{i=1}^{n}|x_{i}-{\hat {\mu }}|$ .

יישום

התפלגות לפלס שימשה בזיהוי דיבור כדי למדל התפלגויות פריוריות על מקדמי התמרת פוריה בזמן בדיד (DFT) ובדחיסת תמונת JPEG.

• הוספה של רעש שנלקח מהתפלגות לפלס, עם פרמטר קנה מידה המתאים לרגישות הפונקציה, לפלט של שאילתת מסד נתונים סטטיסטי היא אמצעי נפוץ לספק פרטיות דיפרנציאלית במסדי נתונים סטטיסטיים.

התפלגות לפלס מותאמת לכמות גשמים מקסימלית של יום אחד

• בניתוח רגרסיה, אומדן הסטיות הפחות אבסולוטיות מתעורר כאומדן הסבירות המקסימלית אם לשגיאות יש התפלגות לפלס.
• ניתן להתייחס ל מודל לאסו כאל רגרסיה בייסיאנית עם הסתברות פריורית לפלס.
• בהידרולוגיה התפלגות לפלס מיושמת לאירועי קיצון כגון כמות גשמים מרבית שנתית של יום אחד וספיקה של נהרות. האיור הכחול, ממחיש דוגמה להתאמת התפלגות לפלס לכמות הגשמים המקסימלית השנתית המדורגת של יום אחד, המציגה גם את רווח בר סמך של 90% על סמך ההתפלגות הבינומית. נתוני הגשמים מיוצגים על ידי התווית מיקומים כחלק מניתוח התדירות המצטבר.
• להתפלגות לפלס יש יישומים בתחום הפיננסים. לדוגמה, מודל למחירי מכשירים פיננסיים המשלב התפלגות לפלס כדי לטפל בבעיות של צידוד, וגבנוניות המתרחשות לעיתים קרובות בעת שימוש בהתפלגות נורמלית לתמחור מכשירים אלה.

התפלגות לפלס, בהיותה התפלגות מורכבת או כפולה, ישימה במצבים שבהם הערכים הנמוכים מקורם בתנאים חיצוניים שונים מהגבוהים כך שהם עוקבים אחר דפוס שונה.

יצירת משתנים מקריים

בהינתן משתנה מקרי $U$ בעל התפלגות אחידה רציפה בקטע $\left(-1/2,1/2\right)$, למשתנה המקרי

$X=\mu -b\,\operatorname {sgn}(U)\,\ln(1-2|U|)$

התפלגות לפלס עם פרמטרים $\mu$ ו $b$. תוצאה זו נובע מפונקציית ההתפלגות המצטברת ההופכית שנתונה לעיל.

היסטוריה

התפלגות לפלס מכונה לעיתים קרובות "חוק השגיאות הראשון של לפלס". פייר סימון לפלס פרסם אותו בשנת 1774, תוך מידול תדירות שגיאה כפונקציה מעריכית של גודל השגיאה בערך מוחלט. לפלס יחליף מאוחר יותר את המודל הזה ב"חוק השגיאות השני" שלו, שהתבסס על ההתפלגות הנורמלית, לאחר גילוי משפט הגבול המרכזי.

ב-1911 פרסם קיינס מאמר המבוסס על התזה המוקדמת שלו, שבה הראה שהתפלגות לפלס מזערה את הסטייה המוחלטת מהחציון.

קישורים חיצוניים

מדיה וקבצים בנושא התפלגות לפלס בוויקישיתוף

• התפלגות לפלס, באתר MathWorld (באנגלית)