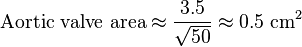Aortic valve area calculation
Aortic valve area calculation is an indirect method of determining the area of the aortic valve. The calculated aortic valve orifice area is currently one of the measures for evaluating the severity of aortic stenosis. A valve area of less than 0.8 cm² is considered to be severe aortic stenosis.[1][2]
There are many ways to calculate the valve area of aortic stenosis. The most commonly used methods involve measurements taken during echocardiography. For interpretation of these values, the area is generally divided by the body surface area, to arrive at the patient's optimal aortic valve orifice area.
Contents
Planimetry
Planimetry is the tracing out of the opening of the aortic valve in a still image obtained during echocardiographic acquisition during ventricular systole, when the valve is supposed to be open. While this method directly measures the valve area, the image may be difficult to obtain due to artifacts during echocardiography, and the measurements are dependent on the technician who has to manually trace the perimeter of the open aortic valve. Because of these reasons, planimetry of aortic valve is not routinely performed.
The continuity equation
The continuity equation states that the flow in one area must equal the flow in a second area if there are no shunts between the two areas. In practical terms, the flow from the left ventricular outflow tract (LVOT) is compared to the flow at the level of the aortic valve. In echocardiography the aortic valve area is calculated using the velocity time integral (VTI) which is the most accurate method and preferred. The flow through the LVOT, or LV Stroke Volume (cm3 or cc), can be calculated by measuring the LVOT diameter (cm), squaring that value, multiplying the value by 0.78540 giving cross sectional area of the LVOT (cm2)and multiplying that value by the LVOT VTI(cm), measured on the spectral Doppler display using pulsed-wave Doppler. From these, it is easy to calculate the area (cm2) of the aortic valve by simply dividing the LV Stroke Volume (cm3) by the AV VTI(cm) measured on the spectral Doppler display using continuous-wave Doppler.
SV = 0.785 x Diameter2 x VTI(LVOT)
CSA(LVOT)cm2 = 0.785 x LVOT Diameter
SV = Stroke Volume CSA = Cross sectional area
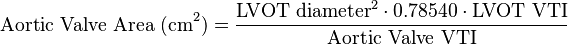
| Example: An individual undergoes transthoracic echocardiography for the evaluation of a systolic ejection murmur with delayed carotid upstroke noted on physical examination. During echocardiography, the following measurements were made: LVOT diameter of 2 cm, LVOT VTI of 24 cm, and an Aortic Valve VTI of 50 cm. What is the aortic valve area? | ||
| Answer: An LVOT diameter of 2 cm gives a LVOT cross-sectional area of, 2 * 2 * 0.78540 = 3.14 cm2. To calculate stroke volume, multiply the cross-sectional area of 3.14 cm2 by the LVOT VTI 24 cm. This gives an LV Stroke Volume of 3.14 * 24 = 75.40 cc. Divide the LV Stroke Volume, 75.40 cc by the Aortic Valve VTI, 50 cm and this gives an aortic valve area of 75.40 / 50 = 1.51 cm2. |
The weakest aspect of this calculation is the variability in measurement of LVOT area, because it involves squaring the LVOT dimension. Therefore, it is crucial for the sonographer to take great care in measuring the LVOT diameter.
The measurement using echocardiogram may be inaccurate in cases of Aortic subvalvular stenosis, because there is not a uniform diameter, as assumed during echocardiogram. The viewpoint of the echocardiogram may distort the true diameter of the LVOT in some patients. For verification purposes of the obtained valve area using echocardiogram and doppler measures, especially if the obtained valve area is in the range requiring surgery and cardiac output is low, the Gold standard of left heart catheterization for true hemodynamics should be obtained for validation using the Gorlin formula, so patient does not go for unneeded surgery.
The Gorlin equation
The Gorlin equation states that the aortic valve area is equal to the flow through the aortic valve during ventricular systole divided by the systolic pressure gradient across the valve times a constant. The flow across the aortic valve is calculated by taking the cardiac output (measured in liters/minute) and dividing it by the heart rate (to give output per cardiac cycle) and then dividing it by the systolic ejection period measured in seconds per beat (to give flow per ventricular contraction).

The Gorlin equation is related to flow across the valve. Because of this, the valve area may be erroneously calculated as stenotic if the flow across the valve is low (i.e. if the cardiac output is low). The measurement of the true gradient is accomplished by temporarily increasing the cardiac output by the infusion of positive inotropic agents, such as dobutamine.
| Example: An individual undergoes left and right heart cardiac catheterization as part of the evaluation of aortic stenosis. The following hemodynamic parameters were measured. With a heart rate of 80 beats/minute and a systolic ejection period of 0.33 seconds, the cardiac output was 5 liters/minute. During simultaneous measurement of pressures in the left ventricle and aorta (with the use of one catheter in the left ventricle and a second in the ascending aorta), the mean systolic pressure gradient was measured at 50 mmHg. What is the valve area as measured by the Gorlin equation? | ||
Answer: 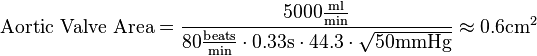 |
The Hakki equation
The Hakki equation[3] is a simplification of the Gorlin equation, relying on the observation that in most cases, the numerical value of 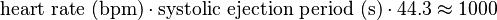 . The resulting simplified formula is:
. The resulting simplified formula is:
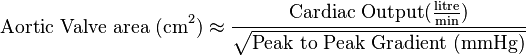
| Example: An individual undergoes left and right cardiac catheterization for the evaluation of aortic stenosis. Measurements includes an aortic pressure of 120/60, LV pressure of 170/15, cardiac output of 3.5 liters/minute. What is the aortic valve area? | ||
| Answer: The peak gradient between the LV and aorta is 50 mmHg. This gives
|
The Agarwal-Okpara-Bao equation
The Agarwal-Okpara-Bao equation is a new form of AVA evaluation equation.[4][5] It was derived from curve fitting of CFD simulation results and 80 clinical data obtained by Minners, Allgeier, Gohlke-Baerwolf, Kienzle, Neumann, and Jander [6] using a multi-objective genetic algorithm. The comparison of the results calculated from Gorlin Equation, Agarwal-Okpara-Bao Equation, and clinical data is shown in the figures on the right.
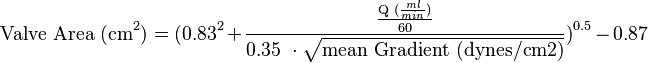
| Example: An individual undergoes left and right cardiac catheterization for the evaluation of aortic stenosis. The following hemodynamic parameters were measured. During simultaneous measurement of pressures in the left ventricle and aorta (with the use of one catheter in the left ventricle and a second in the ascending aorta), the mean systolic pressure gradient was measured at 22665 dynes/cm2. cardiac output of 13440 milliters/minute. What is the aortic valve areas? | ||
Answer: 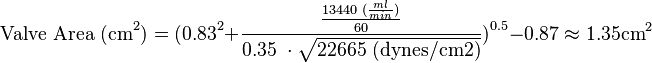 |
References
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.