Consumer price index

"CPI" redirects here. For other uses, see CPI (disambiguation).

A graph of the US CPI from 1913 to 2014 (in blue), and its percentage annual change (in red)

A consumer price index (CPI) measures changes in the price level of a market basket of consumer goods and services purchased by households.

The CPI is a statistical estimate constructed using the prices of a sample of representative items whose prices are collected periodically. Sub-indexes and sub-sub-indexes are computed for different categories and sub-categories of goods and services, being combined to produce the overall index with weights reflecting their shares in the total of the consumer expenditures covered by the index. It is one of several price indices calculated by most national statistical agencies. The annual percentage change in a CPI is used as a measure of inflation. A CPI can be used to index (i.e., adjust for the effect of inflation) the real value of wages, salaries, pensions, for regulating prices and for deflating monetary magnitudes to show changes in real values. In most countries, the CPI is, along with the population census and the USA National Income and Product Accounts, one of the most closely watched national economic statistics.

Introduction

Basic types of data are needed to construct the CPI: price data and weighting data. The price data are collected for a sample of goods and services from a sample of sales outlets in a sample of locations for a sample of times. The weighting data are estimates of the shares of the different types of expenditure in the total expenditure covered by the index. These weights are usually based upon expenditure data obtained from expenditure surveys for a sample of households or upon estimates of the composition of consumption expenditure in the National Income and Product Accounts. Although some of the sampling of items for price collection is done using a sampling frame and probabilistic sampling methods, many items and outlets are chosen in a commonsense way (purposive sampling) that does not permit estimation of confidence intervals. Therefore, the sampling variance cannot be calculated. In any case, a single estimate is required in most of the purposes for which the index is used.

The index is usually computed monthly, or quarterly in some countries, as a weighted average of sub-indices for different components of consumer expenditure, such as food, housing, shoes, clothing, each of which is in turn a weighted average of sub-sub-indices. At the most detailed level, the elementary aggregate level, (for example, men's shirts sold in department stores in San Francisco), detailed weighting information is unavailable, so indices are computed using an unweighted arithmetic or geometric mean of the prices of the sampled product offers. (However, the growing use of scanner data is gradually making weighting information available even at the most detailed level.) These indices compare prices each month with prices in the price-reference month. The weights used to combine them into the higher-level aggregates, and then into the overall index, relate to the estimated expenditures during a preceding whole year of the consumers covered by the index on the products within its scope in the area covered. Thus the index is a fixed-weight index, but rarely a true Laspeyres index, since the weight-reference period of a year and the price-reference period, usually a more recent single month, do not coincide. It takes time to assemble and process the information used for weighting which, in addition to household expenditure surveys, may include trade and tax data.

Ideally, the weights would relate to the composition of expenditure during the time between the price-reference month and the current month. There is a large technical economics literature on index formulae which would approximate this and which can be shown to approximate what economic theorists call a true cost of living index. Such an index would show how consumer expenditure would have to move to compensate for price changes so as to allow consumers to maintain a constant standard of living. Approximations can only be computed retrospectively, whereas the index has to appear monthly and, preferably, quite soon. Nevertheless, in some countries, notably in the United States and Sweden, the philosophy of the index is that it is inspired by and approximates the notion of a true cost of living (constant utility) index, whereas in most of Europe it is regarded more pragmatically.

The coverage of the index may be limited. Consumers' expenditure abroad is usually excluded; visitors' expenditure within the country may be excluded in principle if not in practice; the rural population may or may not be included; certain groups such as the very rich or the very poor may be excluded. Saving and investment are always excluded, though the prices paid for financial services provided by financial intermediaries may be included along with insurance.

The index reference period, usually called the base year, often differs both from the weight-reference period and the price reference period. This is just a matter of rescaling the whole time-series to make the value for the index reference-period equal to 100. Annually revised weights are a desirable but expensive feature of an index, for the older the weights the greater is the divergence between the current expenditure pattern and that of the weight reference-period.

Calculating the CPI for a single item

Current item price ($) = (base year price) * [(Current CPI) / (Base year CPI)]

or

$\frac{CPI_2}{CPI_1}= \frac{Price_2}{Price_1}$

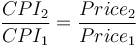
Where 1 is usually the comparison year and CPI₁ is usually an index of 100.

Alternatively, the CPI can be performed as $CPI= \frac{\text{updated cost}}{\text{base period cost}} \times 100$. The "updated cost" (i.e. the price of an item at a given year, e.g.: the price of bread in 2010) is divided by that of the initial year (the price of bread in 1970), then multiplied by one hundred.

Calculating the CPI for multiple items

Many but not all price indices are weighted averages using weights that sum to 1 or 100.

Example: The prices of 85,000 items from 22,000 stores, and 35,000 rental units are added together and averaged. They are weighted this way: Housing: 41.4%, Food and Beverage: 17.4%, Transport: 17.0%, Medical Care: 6.9%, Other: 6.9%, Apparel: 6.0%, Entertainment: 4.4%. Taxes (43%) are not included in CPI computation.

$CPI = (\sum_{i=1}^{n} CPI_i*weight_i)/\sum_{i=1}^{n} weight_i$

where the 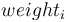$weight_i$s do not necessarily sum to 1 or 100.

Weighting

Weights and sub-indices

By convention weights are fractions or ratios summing to one, as percentages summing to 100 or as per mille numbers summing to 1000.

On the European Union's Harmonised Index of Consumer Prices (HICP), for example, each country computes some 80 prescribed sub-indices, their weighted average constituting the national HICP. The weights for these sub-indices will consist of the sum of the weights of a number of component lower level indices. The classification is according to use, developed in a national accounting context. This is not necessarily the kind of classification that is most appropriate for a Consumer Price Index. Grouping together of substitutes or of products whose prices tend to move in parallel might be more suitable.

For some of these lower level indexes detailed reweighing to make them be available, allowing computations where the individual price observations can all be weighted. This may be the case, for example, where all selling is in the hands of a single national organisation which makes its data available to the index compilers. For most lower level indexes, however, the weight will consist of the sum of the weights of a number of elementary aggregate indexes, each weight corresponding to its fraction of the total annual expenditure covered by the index. An 'elementary aggregate' is a lowest-level component of expenditure, one which has a weight but within which, weights of its sub-components are usually lacking. Thus, for example: Weighted averages of elementary aggregate indexes (e.g. for men's shirts, raincoats, women's dresses, etc.) make up low level indexes (e.g. Outer garments).

Weighted averages of these in turn provide sub-indices at a higher, more aggregated level,(e.g. clothing) and weighted averages of the latter provide yet more aggregated sub-indices (e.g. Clothing and Footwear).

Some of the elementary aggregate indexes, and some of the sub-indexes can be defined simply in terms of the types of goods and/or services they cover, as in the case of such products as newspapers in some countries and postal services, which have nationally uniform prices. But where price movements do differ or might differ between regions or between outlet types, separate regional and/or outlet-type elementary aggregates are ideally required for each detailed category of goods and services, each with its own weight. An example might be an elementary aggregate for sliced bread sold in supermarkets in the Northern region.

Most elementary aggregate indexes are necessarily 'unweighted' averages for the sample of products within the sampled outlets. However, in cases where it is possible to select the sample of outlets from which prices are collected so as to reflect the shares of sales to consumers of the different outlet types covered, self-weighted elementary aggregate indexes may be computed. Similarly, if the market shares of the different types of product represented by product types are known, even only approximately, the number of observed products to be priced for each of them can be made proportional to those shares.

Estimating weights

The outlet and regional dimensions noted above mean that the estimation of weights involves a lot more than just the breakdown of expenditure by types of goods and services, and the number of separately weighted indexes composing the overall index depends upon two factors:

1. The degree of detail to which available data permit breakdown of total consumption expenditure in the weight reference-period by type of expenditure, region and outlet type.
2. Whether there is reason to believe that price movements vary between these most detailed categories.

How the weights are calculated, and in how much detail, depends upon the availability of information and upon the scope of the index. In the UK the Retail Price Index (RPI) does not relate to the whole of consumption, for the reference population is all private households with the exception of a) pensioner households that derive at least three-quarters of their total income from state pensions and benefits and b) "high income households" whose total household income lies within the top four per cent of all households. The result is that it is difficult to use data sources relating to total consumption by all population groups.

For products whose price movements can differ between regions and between different types of outlet:

• The ideal, rarely realisable in practice, would consist of estimates of expenditure for each detailed consumption category, for each type of outlet, for each region.
• At the opposite extreme, with no regional data on expenditure totals but only on population (e.g. 24% in the Northern region) and only national estimates for the shares of different outlet types for broad categories of consumption (e.g. 70% of food sold in supermarkets) the weight for sliced bread sold in supermarkets in the Northern region has to be estimated as the share of sliced bread in total consumption × 0.24 × 0.7.

The situation in most countries comes somewhere between these two extremes. The point is to make the best use of whatever data are available.

The nature of the data used for weighting

No firm rules can be suggested on this issue for the simple reason that the available statistical sources differ between countries. However, all countries conduct periodical Household Expenditure surveys and all produce breakdowns of Consumption Expenditure in their National Accounts. The expenditure classifications used there may however be different. In particular:

• Household Expenditure surveys do not cover the expenditures of foreign visitors, though these may be within the scope of a Consumer Price Index.
• National Accounts include imputed rents for owner-occupied dwellings which may not be within the scope of a Consumer Price Index.

Even with the necessary adjustments, the National Account estimates and Household Expenditure Surveys usually diverge.

The statistical sources required for regional and outlet-type breakdowns are usually weaker. Only a large-sample Household Expenditure survey can provide a regional breakdown. Regional population data are sometimes used for this purpose, but need adjustment to allow for regional differences in living standards and consumption patterns. Statistics of retail sales and market research reports can provide information for estimating outlet-type breakdowns, but the classifications they use rarely correspond to COICOP categories.

The increasingly widespread use of bar codes, scanners in shops has meant that detailed cash register printed receipts are provided by shops for an increasing share of retail purchases. This development makes possible improved Household Expenditure surveys, as Statistics Iceland has demonstrated. Survey respondents keeping a diary of their purchases need to record only the total of purchases when itemised receipts were given to them and keep these receipts in a special pocket in the diary. These receipts provide not only a detailed breakdown of purchases but also the name of the outlet. Thus response burden is markedly reduced, accuracy is increased, product description is more specific and point of purchase data are obtained, facilitating the estimation of outlet-type weights.

There are only two general principles for the estimation of weights: use all the available information and accept that rough estimates are better than no estimates.

Reweighting

Ideally, in computing an index, the weights would represent current annual expenditure patterns. In practice they necessarily reflect past using the most recent data available or, if they are not of high quality, some average of the data for more than one previous year. Some countries have used a three-year average in recognition of the fact that household survey estimates are of poor quality. In some cases some of the data sources used may not be available annually, in which case some of the weights for lower level aggregates within higher level aggregates are based on older data than the higher level weights.

Infrequent reweighing saves costs for the national statistical office but delays the introduction into the index of new types of expenditure. For example, subscriptions for Internet Service entered index compilation with a considerable time lag in some countries, and account could be taken of digital camera prices between re-weightings only by including some digital cameras in the same elementary aggregate as film cameras.

Owner-occupiers and the price index

The way in which owner-occupied dwellings should be dealt with in a Consumer Price Index has been, and remains, a subject of heated controversy in many countries. Various approaches have been considered, each with their advantages and disadvantages.

The economists' approach

See also: Imputed rent

Leaving aside the quality of public services, the environment, crime and so forth, and regarding the standard of living as a function of the level and composition of individuals' consumption, this standard depends upon the amount and range of goods and services they consume. These include the service provided by rented accommodation, which can readily be priced, and the similar services yielded by a flat or house owned by the consumer who occupies it. Its cost to a consumer is, according to the economic way of thinking, an "opportunity cost", namely what he or she sacrifices by living in it. This cost, according to many economists, is what should form a component of a Consumer Price Index.

Opportunity cost can be looked at in two ways, since there are two alternatives to continuing to live in an owner-occupied dwelling. One — supposing that it is one year's cost that is to be considered — is to sell it, earn interest on the owner's capital thus released, and buy it back a year later, making an allowance for its physical depreciation. This can be called the "alternative cost" approach. The other, the "rental equivalent" approach, is to let it to someone else for the year, in which case the cost is the rent that could be obtained for it.

There are, of course, practical problems in implementing either of these economists' approaches. Thus, with the alternative cost approach, if house prices are rising fast the cost can be negative and then become sharply positive once house prices start to fall, so such an index would be very volatile. On the other hand, with the rental equivalent approach, there may be difficulty in estimating the movement of rental values of types of property which are not actually rented. If one or other of these measures of the consumption of the services of owner-occupied dwellings is included in consumption, then it must be included in income too, for income equals consumption plus saving. This means that if the movement of incomes is to be compared with the movement of the Consumer Price Index, incomes must be expressed as money income plus this imaginary consumption value. That is logical, but it may not be what users of the index want.

Although the argument has been expressed in connection with owner-occupied dwellings, the logic applies equally to all durable consumer goods and services. Furniture, carpets and domestic appliances are not used up soon after purchase in the way that food is. Like dwellings, they yield a consumption service that can continue for years. Furthermore, since strict logic is to be adhered to, there are durable services as well that ought to be treated in the same way; the service consumers derive from appendectomies or crowned teeth continue for a long time. Since estimating values for these components of consumption has not been tackled, the economic theorists are torn between their desire for intellectual consistency and their recognition that inclusion of the opportunity cost of the use of durables is impracticable.

Spending

Another approach is to concentrate on spending.[3] Everyone agrees that repairs and maintenance expenditure of owner-occupied dwellings should be covered in a Consumer Price Index, but the spending approach would include mortgage interest too. This turns out to be quite complicated, conceptually as well as in practice.

To explain what is involved, consider a Consumer Price Index computed with reference to 2009 for just one sole consumer who bought her house in 2006, financing half of this sum by raising a mortgage. The problem is to compare how much interest such a consumer would now be paying with the interest that was paid in 2009. Since the aim is to compare like with like, that requires an estimate of how much interest would be paid now in the year 2010 on a similar house bought and 50% mortgage-financed three years ago, in 2007. It does not require an estimate of how much that identical person is paying now on the actual house she bought in 2006, even though that is what personally concerns her now.

A Consumer Price Index compares how much it would cost now to do exactly what consumers did in the reference-period with what it cost then. Application of the principle thus requires that the index for our one house owner should reflect the movement of the prices of houses like hers from 2006 to 2007 and the change in interest rates. If she took out a fixed-interest rate mortgage it is the change in interest rates from 2006 to 2007 that counts; if she took out a variable interest mortgage it is the change from 2009 to 2010 that counts. Thus her current index with 1999 as reference-period will stand at more than 100 if house prices or, in the case of a fixed-interest mortgage, interest rates rose between 2006 and 2007.

The application of this principle in the owner-occupied dwellings component of a Consumer Price Index is known as the "debt profile" method. It means that the current movement of the index will reflect past changes in dwelling prices and interest rates. Some people regard this as odd. Quite a few countries use the debt profile method, but in doing so most of them behave inconsistently. Consistency would require that the index should also cover the interest on consumer credit instead of the whole price paid for the products bought on credit if it covers mortgage interest payments. Products bought on credit would then be treated in the same way as owner-occupied dwellings.

Variants of the debt profile method are employed or have been proposed. One example is to include down payments as well as interest. Another is to correct nominal mortgage rates for changes in dwelling prices or for changes in the rest of the Consumer Price Index to obtain a "real" rate of interest. Also, other methods may be used alongside the debt profile method. Thus several countries include a purely notional cost of depreciation as an additional index component, applying an arbitrarily estimated, or rather guessed, depreciation rate to the value of the stock of owner-occupied dwellings. Finally, one country includes both mortgage interest and purchase prices in its index.

Transaction prices

The third approach simply treats the acquisition of owner-occupied dwellings in the same way as acquisitions of other durable products are treated. This means: Taking account of the transaction prices agreed;

• Ignoring whether payments are delayed or are partly financed by borrowing;
• Leaving out second-hand transactions. Second-hand purchases correspond to sales by other consumers. Thus only new dwellings would be included.

Furthermore, expenditure on enlarging or reconstructing an owner-occupied dwelling would be covered, in addition to regular maintenance and repair. Two arguments of an almost theological character are advanced in connection with this transactions approach.

One argument is that purchases of new dwellings are treated as Investment in the System of National Accounts, so should not enter a consumption price index. It is said that this is more than just a matter of terminological uniformity. For example it may be thought to help understanding and facilitate economic analysis if what is included under the heading of Consumption is the same in the Consumer Price Index and in the national income and expenditure accounts. Since these accounts include the equivalent rental value of owner-occupied dwellings, the equivalent rental approach would have to be applied in the Consumer Price Index too. But the national accounts do not apply it to other durables, so the argument demands consistency in one respect but accepts its rejection in another.

The other argument is that the prices of new dwellings should exclude that part reflecting the value of the land, since this is an irreproducible and permanent asset that cannot be said to be consumed. This would presumably mean deducting site value from the price of a dwelling, site value presumably being defined as the price the site would fetch at auction if the dwelling were not on it. How this is to be understood in the case of multiple dwellings remains unclear.

Confusion

It is apparent that much of the muddle in discussing the merits of the different approaches arises from the promiscuous mixing up of arguments about feasibility, about dislike or approval of the way the index would move under a particular approach and about principles of various, often incompatible, sorts. Feasibility is naturally important. The difficulty of dealing with site values is obvious.

Statisticians in a country lacking a good dwelling price index (which is required for all except the rental equivalent method) will go along with a proposal to use such an index only if they can obtain the necessary additional resources that will enable them to compile one. Even obtaining mortgage interest rate data can be a major task in a country with a multitude of mortgage lenders and many types of mortgage. Dislike of the effect upon the behaviour of the Consumer Price Index arising from the adoption of some methods can be a powerful, if sometimes unprincipled, argument.

Dwelling prices are volatile and so, therefore, would be an index incorporating the current value of a dwelling price sub-index which, in some countries, would have a large weight under the third approach. Furthermore, the weight for owner-occupied dwellings could be altered considerably when reweighting was undertaken. (It could even become negative under the alternative cost approach if weights were estimated for a year during which house prices had been rising steeply).

Then, there is the point that a rise in interest rates designed to halt inflation could paradoxically make inflation appear higher if current interest rates showed up in the index. Economists' principles are not acceptable to all; nor is insistence upon consistency between the treatment of owner-occupied dwellings and other durables.

Consumer Price Indices in the United States

Main article: United States Consumer Price Index

In the United States, several different consumer price indices are routinely computed by the Bureau of Labor Statistics (BLS). These include the CPI-U (for all urban consumers), CPI-W (for Urban Wage Earners and Clerical Workers), CPI-E (for the elderly), and C-CPI-U (chained CPI for all urban consumers). These are all built in two stages. First, the BLS collects data to estimate 8,018 separate item-area indices reflecting the prices of 211 categories of consumption items in 38 geographical areas. In the second stage, weighted averages are computed of these 8,018 item-area indices. The different indices differ only in the weights applied to the different 8,018 item-area indices. The weights for CPI-U and CPI-W are held constant for 24 months, changing in January of even-numbered years. The weights for C-CPI-U are updated each month to reflecting changes in consumption patterns in the last month. Thus, if people on average eat more chicken and less beef or more apples and fewer oranges than the previous month, that change would be reflected in next month's C-CPI-U. However, it would not be reflected in CPI-U and CPI-W until January of the next even-numbered year.

This allows the BLS to compute consumer price indices for each of the designated 38 geographical areas and for aggregates like the Midwest.

In January of each year, Social Security recipients receive a cost of living adjustment (COLA) "to ensure that the purchasing power of Social Security and Supplemental Security Income (SSI) benefits is not eroded by inflation. It is based on the percentage increase in the Consumer Price Index for Urban Wage Earners and Clerical Workers (CPI-W)". The use of CPI-W conflicts with this purpose, because the elderly consume substantially more health care goods and services than younger people. In recent years, inflation in health care has substantially exceeded inflation in the rest of the economy. Since the weight on health care in CPI-W is much less than the consumption patterns of the elderly, this COLA does not adequately compensate them for the real increases in the costs of the items they buy.

The BLS does track a consumer price index for the elderly (CPI-E). It is not used, in part because the social security trust fund is forecasted to run out of money in roughly 40 years, and using the CPI-E instead of CPI-W would shorten that by roughly 5 years.

History

Between 1971 and 1977, the United States CPI increased 47%.

In 2009, the Consumer Price Index fell for the first time since 1955.

Chained CPI

Main article: United States Chained Consumer Price Index

Former White House Chief of Staff Erskine Bowles and former U.S. Senator Alan K. Simpson suggested a transition to using a "chained CPI" in 2010, when they headed the White House's deficit-reduction commission. They stated that it was a more accurate measure of inflation than the current system and switching from the current system could save the government more than $290 billion over the decade following their report. "The chained CPI is usually 0.25 to 0.30 percentage points lower each year, on average, than the standard CPI measurements".

However, the National Active and Retired Federal Employees Associations said that the chained CPI does not account for seniors citizens' health care costs. Robert Reich, former United States Secretary of Labor under President Clinton, noted that typical seniors spend between 20 and 40 percent of their income on health care, far more than most Americans. "Besides, Social Security isn't in serious trouble. The Social Security trust fund is flush for at least two decades. If we want to ensure it's there beyond that, there's an easy fix – just lift the ceiling on income subject to Social Security taxes, which is now $113,700."

Replacing the current cost-of-living adjustment calculation with the chained CPI was considered, but not adopted, as part of a deficit-reduction proposal to avert the sequestration cuts, or fiscal cliff, in January 2013, but President Obama included it in his April 2013 budget proposal.

See also

• Consumer price index by country
• Core inflation
• Cost of living index
• FRED (Federal Reserve Economic Data)
• Harmonized Index of Consumer Prices (HICP)
• Hedonic regression
• Higher Education Price Index
• Household final consumption expenditure (HFCE)
• GDP deflator
• Inflation adjustment
• Inflation rate
• Inflationism
• List of economics topics
• Market basket (basket of goods)
• MIT Billion Prices project
• Personal consumption expenditures price index (PCEPI)
• Producer Price Index (PPI)
• Quality bias
• RPIX
• World inflation crisis

Further reading

• W.E. Diewert, 1993. The early history of price index research. Chapter 2 of Essays in Index Number Theory, Volume I, W.E. Diewert and A.O. Nakamura, editors. Elsevier Science Publishers, B.V.

External links

• Issues of the Consumer Price Index report from the BLS for 1953–1974 and 1974–present
• ILO CPI manual – This large manual produced co-operatively by a number of international organizations is the standard work on the methods of compiling consumer price indexes and on the underlying economic and statistical theory.
• myCPI.info – Project for establishing alternative CPI data based on users inputting and tracking their personal CPI.
• "The Consumer Price Index and index number purpose" – A technical article by economist W.E. Diewert
• SGS Alternate Inflation Charts
• SGS CPI calculation criticisms
• BLS rebuttal to SGS CPI calculation criticisms
• SGS rebuttal to BLS rebuttal regarding CPI
• CPI Inflation Calculator

Specific countries

International

• Worldwide Consumer Price Index Per City User-Updated
• User contributed cost of living database

Australia

• Australian CPI
• Measures of Consumer Price Inflation

France

• Consumer Price Index, INSEE
• A description of the French consumer price index (in French)
• French CPI composition and evolution

Canada

• Statistics Canada

Hong Kong

• Hong Kong Consumer Price Index (CPI), Census and Statistics Department

India

• CPI and its composition in India

Italy

• Indici dei prezzi al consumo, ISTAT
• Rivalutazione monetaria con gli Indici dei prezzi al consumo per le famiglie di operai ed impiegati

Spain

• CPI information, Instituto Nacional de Estadística

New Zealand

• CPI information, Statistics New Zealand

Sweden

• A Consumer Price Index for Sweden 1290–2006
• A detailed account in English of the Swedish consumer price index

Denmark

• Oldmoney.dk – A Consumer Price Index-calculator for Denmark 1900–2010

United Kingdom

• Consumer Price Indices, A brief guide , UK Office for National Statistics
• National Statistics Online: Consumer Prices, UK Office for National Statistics
• A detailed account of the UK index

United States

• Consumer Price Index Home Page, U.S. Department of Labor, Bureau of Labor Statistics
• A detailed account of the US index
• Inflation Calculator
• CPI categories 1993–2010
• Alternate non official CPI measures
• An inflation research site and personal inflation rate calculator
• Consumer Price Index 1953–1974 and CPI Detailed Report 1974–present – historical Bureau of Labor Statistics publications digitized for Federal Reserve Archival System for Economic Research