Decision rule

This article is about decision theory. For the use in computer science, see Decision tree § Decision rules.

In decision theory, a decision rule is a function which maps an observation to an appropriate action. Decision rules play an important role in the theory of statistics and economics, and are closely related to the concept of a strategy in game theory.

In order to evaluate the usefulness of a decision rule, it is necessary to have a loss function detailing the outcome of each action under different states.

Formal definition

Given an observable random variable X over the probability space 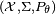$\scriptstyle (\mathcal{X},\Sigma, P_\theta)$, determined by a parameter θ ∈ Θ, and a set A of possible actions, a (deterministic) decision rule is a function δ : 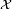$\scriptstyle\mathcal{X}$→ A.

Examples of decision rules

• An estimator is a decision rule used for estimating a parameter. In this case the set of actions is the parameter space, and a loss function details the cost of the discrepancy between the true value of the parameter and the estimated value. For example, in a linear model with a single scalar parameter 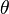$\theta$, the domain of 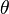$\theta$ may extend over 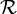$\mathcal{R}$ (all real numbers). 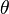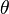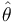An associated decision rule for estimating $\theta$ from some observed data might be, "choose the value of the $\theta$, say $\hat{\theta}$, that minimizes the sum of squared error between some observed responses and responses predicted from the corresponding covariates given that you chose 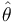$\hat{\theta}$." Thus, the cost function is the sum of squared error, and one would aim to minimize this cost. Once the cost function is defined, 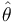$\hat{\theta}$ could be chosen, for instance, using some optimization algorithm.
• Out of sample prediction in regression and classification models.

See also

• Admissible decision rule
• Bayes estimator