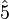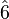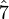Diminished triad

From Infogalactic: the planetary knowledge core
Jump to: navigation, search
diminished triad
Component intervals from root
diminished fifth (tritone)
minor third
root
Tuning
45:54:64;[1] 54:45=6:5 & 64:45[2]
Forte no. / Complement
3-10 / 9-10
Diminished triad on B <phonos file="Diminished triad on B.mid">play</phonos> or <phonos file="Diminished triad on B just.mid">Play just</phonos>.
Dominant seventh and incomplete dominant seventh in C major: G7 and bo chords <phonos file="Incomplete dominant seventh chord in C major.mid">Play</phonos>.

In music, a diminished triad (<phonos file="Diminished triad on B.mid">Play</phonos>), also known as the minor flatted fifth (m♭5), is a triad consisting of two minor thirds above the root — if built on C, a diminished triad would have a C, an E♭ and a G♭.[3] It resembles a minor triad with a lowered (flattened) fifth. It can be represented by the integer notation {0, 3, 6}.

Diminished triad on C <phonos file="Diminished triad on C.mid">play</phonos>.
iio6 in C minor <phonos file="iidim6 in C.mid">play</phonos>: first inversion do chord.

In the common practice period, the diminished triad is considered dissonant, or unstable, because the dissonant diminished fifth symmetrically divides the octave. The lack of tonal center or stability, possession of a leading-tone, and the dominant function give the chord drive.

Harmonic considerations

A diminished triad occurs in a major scale only on the seventh scale degree; in the key of C, this is a B diminished triad (B, D, F). Since the triad is built on the seventh scale degree, it is also called the leading-tone triad. The leading-tone triad also occurs in the seventh chord built on the fifth degree; in C, this is G dominant seventh (G, B, D, F). For this reason, it has dominant function. Unlike the dominant triad or dominant seventh, the leading-tone triad functions as a prolongational chord rather than a structural chord since the strong root motion by fifth is now absent.[4]

On the other hand, the diminished triad in a minor scale occurs on the second scale degree; in the key of C minor, this is the D diminished triad (D, F, A♭). This triad is consequently called the supertonic diminished triad. Like the supertonic triad found in a major key, the supertonic diminished triad has a predominant function, almost always resolving to a dominant functioning chord.[5]

In a twelve-tone equal tempered tuning, a diminished triad has 3 semitones between the third and fifth, 3 between the root and third, and 6 between the root and fifth. It is represented by the integer notation {0, 3, 6}. In 5-limit just intonation the diminished chord on VII (in C: B-D-F) is 15:8, 9:8, and 4:3, while on II (in C: D-F-A♭) it is 9:8, 4:3, and 8:5 (135:160:192). According to Sorge, the trumpet, in its overtone series on C, gives the diminished triad e-g-b♭ = 5:6:7 ("perfect diminished chord"[6]), but the 7 is too flat and 45:54:64 is preferred.[1] Helmholtz describes the diminished triad as b1−d | f, giving a just minor third and Pythagorean minor third (45:54:64) in the notation system used in On the Sensations of Tone as a Physiological Basis for the Theory of Music.[7] Play <phonos file="Perfect diminished chord on C.mid">Perfect</phonos>, <phonos file="Preferred diminished chord on C.mid">Preferred</phonos> (5-limit major), or <phonos file="Five-limit minor diminished chord on C.mid">5-limit minor</phonos> on C.

Sorge (perfect)/
7-limit		 Sorge (preferred)/
5-limit major		 5-limit minor
(D,F,Ab)
Harmonics
Root E 5 386.31 F♯+ 45 590.22 C# 135 92.18
Third G 6 701.96 A+ 54 905.87 E 160 386.31
Fifth B7♭ 7 968.83 C 64 1200 G 192 701.96
On B
Root B 15:8 1088.27 B 15:8 1088.27 B 15:8 1088.27
Third D 9:8 203.91 D 9:8 203.91 D- 10:9 182.40
Fifth F7+ 21:16 470.78 F 4:3 498.04 F 4:3 498.04
On C
Root C 1:1 0 C 1:1 0 C 1:1 0
Third Eb 6:5 315.64 Eb 6:5 315.64 Eb- 32:27 294.13
Fifth G7b 7:4 582.51 Gb- 64:45 609.78 Gb- 64:45 609.78

In some sheet music books[citation needed], Cdim or C° denotes a diminished seventh chord (a four note chord) with root C, and Cm-5 or Cm♭5 denotes a diminished triad with root C. However, in some modern jazz books and some music theory literature[citation needed], Cdim or C° denotes a diminished triad, while Cdim7 or C°7 denotes a diminished seventh chord.

The supertonic diminished triad and leading-tone diminished triad are usually found in first inversion (iio6 and viio6 respectively) since the spelling of the chord forms a diminished fifth with the bass.[4] This differs from the fully diminished seventh chord, which commonly occurs in root position.[8] In both cases resolve the bass up and move the upper voices downwards in contrary motion.[8] The popular music symbol for a diminished triad is a capital letter designating the root (as with a major chord) with MI(♭5) added.[9] For example BMI(♭5) (see also Chord names and symbols (jazz and pop music)).

Diminished triad substituting for dominant chord in Bach's Well-Tempered Clavier I, Prelude in G Major.[10] <phonos file="Bach - WTC I, Prelude in G Major diminished chord.mid">Play</phonos> or <phonos file="Bach_WTK1_P&F_No15_G-Dur_BWV860.ogg">Play</phonos>

In popular music

"In rock and pop music, the diminished triad nearly always appears on the second scale degree, forming a generally maudlin and dejected iio with its members, 2—4—♭6."[11] Songs that feature iio include Santo & Johnny's Sleep Walk, Jay and the Americans' "Cara Mia", and The Hollies' "The Air That I Breathe".[11] Not so rare but rare enough so as to imply knowledge of and conscious avoidance on the part of rock musicians, examples of its use include Oasis' "Don't Look Back In Anger", David Bowie's "Space Oddity", and two in Paul Young's "Everytime You Go Away".[12]

Diminished chord table

Chord Root Minor Third Diminished Fifth
Cdim(Cm(♭5)) C E♭ G♭
C♯dim(C♯m(♭5)) C♯ E G
D♭dim(D♭m(♭5)) D♭ F♭ (E) Adouble flat (G)
Ddim(Dm(♭5)) D F A♭
D♯dim(D♯m(♭5)) D♯ F♯ A
E♭dim(E♭m(♭5)) E♭ G♭ Bdouble flat (A)
Edim(Em(♭5)) E G B♭
Fdim(Fm(♭5)) F A♭ C♭ (B)
F♯dim(F♯m(♭5)) F♯ A C
G♭dim(G♭m(♭5)) G♭ Bdouble flat (A) Ddouble flat (C)
Gdim(Gm(♭5)) G B♭ D♭
G♯dim(G♯m(♭5)) G♯ B D
A♭dim(A♭m(♭5)) A♭ C♭ (B) Edouble flat (D)
Adim(Am(♭5)) A C E♭
A♯dim(A♯m(♭5)) A♯ C♯ E
B♭dim(B♭m(♭5)) B♭ D♭ F♭ (E)
Bdim(Bm(♭5)) B D F

See also

Sources

  1. ↑ 1.0 1.1 Shirlaw, Matthew (2012). The Theory of Harmony, p.304. Forgotten Books. ISBN 978-1-4510-1534-8.
  2. ↑ Partch, Harry (1979). Genesis of a Music, p.68-69. ISBN 978-0-306-80106-8.
  3. ↑ Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.68. Seventh Edition. ISBN 978-0-07-294262-0.
  4. ↑ 4.0 4.1 Lua error in package.lua at line 80: module 'strict' not found.
  5. ↑ Lua error in package.lua at line 80: module 'strict' not found.
  6. ↑ Fétis, François-Joseph and Arlin, Mary I. (1994). Esquisse de l'histoire de l'harmonie, p.139n9. ISBN 978-0-945193-51-7.
  7. ↑ Hermann von Helmholtz (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music, p.344. Longmans, Green.
  8. ↑ 8.0 8.1 Benward & Saker (2009). Music in Theory and Practice: Volume II, p.76. Eighth Edition. ISBN 978-0-07-310188-0.
  9. ↑ Benward & Saker (2003), p.77.
  10. ↑ Jonas, Oswald (1982). Introduction to the Theory of Heinrich Schenker (1934: Das Wesen des musikalischen Kunstwerks: Eine Einführung in Die Lehre Heinrich Schenkers), p.25. Trans. John Rothgeb. ISBN 0-582-28227-6.
  11. ↑ 11.0 11.1 Everett, Walter (2009). The Foundations of Rock, p.195. ISBN 978-0-19-531023-8.
  12. ↑ Stephenson, Ken (2002). What to Listen for in Rock: A Stylistic Analysis, p.85. ISBN 978-0-300-09239-4.
Retrieved from "https://infogalactic.com/w/index.php?title=Diminished_triad&oldid=712686365"