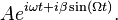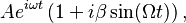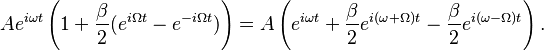Electro-optic modulator

An optical intensity modulator for optical telecommunications

Electro-optic modulator (EOM) is an optical device in which a signal-controlled element exhibiting the electro-optic effect is used to modulate a beam of light. The modulation may be imposed on the phase, frequency, amplitude, or polarization of the beam. Modulation bandwidths extending into the gigahertz range are possible with the use of laser-controlled modulators.

The electro-optic effect is the change in the refractive index of a material resulting from the application of a DC or low-frequency electric field. This is caused by forces that distort the position, orientation, or shape of the molecules constituting the material. Generally, a nonlinear optical material (organic polymers have the fastest response rates, and thus are best for this application) with an incident static or low frequency optical field will see a modulation of its refractive index.

The simplest kind of EOM consists of a crystal, such as lithium niobate, whose refractive index is a function of the strength of the local electric field. That means that if lithium niobate is exposed to an electric field, light will travel more slowly through it. But the phase of the light leaving the crystal is directly proportional to the length of time it takes that light to pass through it. Therefore, the phase of the laser light exiting an EOM can be controlled by changing the electric field in the crystal.

Note that the electric field can be created by placing a parallel plate capacitor across the crystal. Since the field inside a parallel plate capacitor depends linearly on the potential, the index of refraction depends linearly on the field (for crystals where Pockels effect dominates), and the phase depends linearly on the index of refraction, the phase modulation must depend linearly on the potential applied to the EOM.

The voltage required for inducing a phase change of 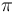$\pi$ is called the half-wave voltage ($V_{\pi}$). For a Pockels cell, it is usually hundreds or even thousands of volts, so that a high-voltage amplifier is required. Suitable electronic circuits can switch such large voltages within a few nanoseconds, allowing the use of EOMs as fast optical switches.

Liquid crystal devices are electro-optical phase modulators if no polarizers are used.

Phase Modulation

A very common application of EOMs is for creating sidebands in a monochromatic laser beam. To see how this works, first imagine that the strength of a laser beam with frequency $\omega$ entering the EOM is given by

$Ae^{i\omega t}.$

Now suppose we apply a sinusoidally varying potential voltage to the EOM with frequency 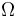$\Omega$ and small amplitude 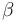$\beta$. This adds a time dependent phase to the above expression,

$Ae^{i\omega t + i\beta\sin(\Omega t)}.$

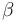Since $\beta$ is small, we can use the Taylor expansion for the exponential

$Ae^{i\omega t}\left( 1+i\beta\sin(\Omega t)\right) ,$

to which we apply a simple identity for sine,

$Ae^{i\omega t}\left( 1+\frac{\beta}{2}(e^{i\Omega t} - e^{-i\Omega t})\right) = A\left( e^{i\omega t}+\frac{\beta}{2}e^{i(\omega+\Omega) t}-\frac{\beta}{2}e^{i(\omega-\Omega) t}\right) .$

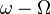This expression we interpret to mean that we have the original carrier signal plus two small sidebands, one at $\omega+\Omega$ and another at $\omega-\Omega$. Notice however that we only used the first term in the Taylor expansion - in truth there are an infinite number of sidebands. There is a useful identity involving Bessel functions called the Jacobi-Anger expansion which can be used to derive

$Ae^{i\omega t + i\beta\sin(\Omega t)} = Ae^{i\omega t}\left( J_0(\beta) + \sum_{k=1}^{\infty}J_k(\beta)e^{ik\Omega t} + \sum_{k=1}^{\infty}(-1)^k J_k(\beta)e^{-ik\Omega t}\right) ,$

which gives the amplitudes of all the sidebands. Notice that if one modulates the amplitude instead of the phase, one gets only the first set of sidebands,

$\left( 1 + \beta\sin(\Omega t)\right) Ae^{i\omega t} = Ae^{i\omega t} + \frac{A\beta}{2i}\left( e^{i(\omega+\Omega) t} - e^{i(\omega-\Omega)t} \right) .$

Amplitude modulation

A phase modulating EOM can also be used as an amplitude modulator by using a Mach-Zehnder interferometer. A beam splitter divides the laser light into two paths, one of which has a phase modulator as described above. The beams are then recombined. Changing the electric field on the phase modulating path will then determine whether the two beams interfere constructively or destructively at the output, and thereby control the amplitude or intensity of the exiting light. This device is called a Mach-Zehnder modulator.

Polarization modulation

Depending on the type and orientation of the nonlinear crystal, and on the direction of the applied electric field, the phase delay can depend on the polarization direction. A Pockels cell can thus be seen as a voltage-controlled waveplate, and it can be used for modulating the polarization state. For a linear input polarization (often oriented at 45° to the crystal axis), the output polarization will in general be elliptical, rather than simply a linear polarization state with a rotated direction.

See also

• Pockels effect
• Acousto-optic modulator
• Phase modulation
• Dielectric wireless receiver

References

•  This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).

External links

• AdvR - Research and custom EO phase and amplitude modulators
• Encyclopedia of Laser Physics and Technology
• Interactive visualization of the transfer characteristic of a Mach-Zehnder modulator for phase and amplitude modulation