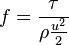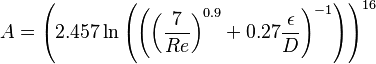Fanning friction factor

The Fanning friction factor, named after John Thomas Fanning, is a dimensionless number used as a local parameter in continuum mechanics calculations. It is defined as the ratio between the local shear stress and the local flow kinetic energy density:

$f = \frac {\tau}{\rho \frac {u^2} 2}$

where:

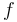• $f$ is the local Fanning friction factor
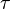• $\tau$ is the local shear stress
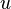• $u$ is the local flow velocity
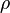• $\rho$ is the density of the fluid

In particular the shear stress at the wall can, in turn, be related to the pressure loss by multiplying the wall shear stress by the wall area (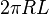$2 \pi R L$ for a pipe with circular cross section) and dividing by the cross-sectional flow area (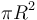$\pi R^2$ for a pipe with circular cross section). Thus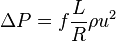 $\Delta P = f \frac{L}{R} \rho u^2$

The friction head can be related to the pressure loss due to friction by dividing the pressure loss by the product of the acceleration due to gravity and the density of the fluid. Accordingly, the relationship between the friction head and the Fanning friction factor is:

$\Delta h = f \frac{u^2 L}{gR}$

where:

• $\Delta h$ is the friction loss (in head) of the pipe.
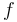• $f$ is the Fanning friction factor of the pipe.
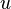• $u$ is the flow velocity in the pipe.
• $L$ is the length of pipe.
• $g$ is the local acceleration of gravity.
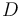• $D$ is the pipe diameter.

Fanning friction factor formula

This friction factor is one-fourth of the Darcy friction factor, so attention must be paid to note which one of these is meant in the "friction factor" chart or equation consulted. Of the two, the Fanning friction factor is the more commonly used by chemical engineers and those following the British convention.

The formulae below may be used to obtain the Fanning friction factor for common applications.

The friction factor for laminar flow in round tubes is often taken to be:

$f= \frac{16}{Re}$

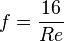
where Re is the Reynolds number of the flow.

For a square channel the value used is:

$f = \frac{14.227}{Re}$

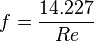
The Darcy friction factor can also be expressed as

$f = \frac{8 \bar \tau}{\rho \bar u ^ 2}$

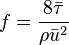
where:

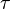• $\tau$ is the shear stress at the wall
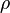• $\rho$ is the density of the fluid
• $\bar u$ is the flow velocity averaged on the flow cross section

For the turbulent flow regime, the relationship between the Fanning friction factor and the Reynolds number is more complex and is governed by the Colebrook equation which is implicit in 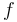$f$:

${1 \over \sqrt{\mathit{f}}}= -4.0 \log_{10} \left(\frac{\frac{\epsilon}{d}}{3.7} + {\frac{1.256}{Re \sqrt{\mathit{f} } } } \right) , \text{turbulent flow}$

Various explicit approximations of the related Darcy friction factor have been developed for turbulent flow.

Stuart W. Churchill developed a formula that covers the friction factor for both laminar and turbulent flow. This was originally produced to describe the Moody chart, which plots the Darcy-Weisbach Friction factor against Reynolds number. The Darcy Weisbach Formula 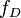$f_D$ is 4 times the Fanning friction factor 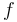$f$ and so a factor of 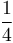$\frac{1}{4}$ has been applied to produce the formula given below.

• Re, Reynolds number (unitless);
• ε, roughness of the inner surface of the pipe (dimension of length);
• D, inner pipe diameter;

$f = 2 \left( \left( \frac {8} {Re} \right) ^ {12} + \left( A+B \right) ^ {-1.5} \right) ^ {\frac {1} {12} }$

$A = \left( 2.457 \ln \left( \left( \left( \frac {7} {Re} \right) ^ {0.9} + 0.27 \frac {\epsilon} {D} \right)^ {-1}\right) \right) ^ {16}$

$B = \left( \frac {37530} {Re} \right) ^ {16}$