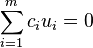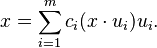John ellipsoid

In mathematics, the John ellipsoid or Löwner-John ellipsoid E(K) associated to a convex body K in n-dimensional Euclidean space Rⁿ is the ellipsoid of maximal n-dimensional volume contained within K. The John ellipsoid is named after the German mathematician Fritz John. The following refinement of John's original theorem, due to Ball (1992), gives necessary and sufficient conditions for the John ellipsoid of K to be the closed unit ball B of Rⁿ:

The John ellipsoid E(K) of a convex body K ⊂ Rⁿ is B if and only if B ⊆ K and there exists an integer m ≥ n and, for i = 1, ..., m, real numbers c_i > 0 and unit vectors u_i ∈ Sⁿ⁻¹ ∩ ∂K such that

$\sum_{i = 1}^{m} c_{i} u_{i} = 0$

and, for all x ∈ Rⁿ

$x = \sum_{i = 1}^{m} c_{i} (x \cdot u_{i}) u_{i}.$

Applications

• Obstacle Collision Detection
• Portfolio optimization policy approximation

See also

• Steiner inellipse, the special case of the John ellipsoid for a triangle

References

• John, Fritz. "Extremum problems with inequalities as subsidiary conditions". Studies and Essays Presented to R. Courant on his 60th Birthday, January 8, 1948, 187—204. Interscience Publishers, Inc., New York, N. Y., 1948. OCLC 1871554 MR 30135