Local convex hull
Local convex hull (LoCoH) is a method for estimating size of the home range of an animal or a group of animals (e.g. a pack of wolves, a pride of lions, or herd of buffaloes), and for constructing a utilization distribution. [1][2] The latter is a probability distribution that represents the probabilities of finding an animal within a given area of its home range at any point in time; or, more generally, at points in time for which the utilization distribution has been constructed. In particular, different utilization distributions can be constructed from data pertaining to particular periods of a diurnal or seasonal cycle.
Utilization distributions are constructed from data providing the location of an individual or several individuals in space at different points in time by associating a local distribution function with each point and then summing and normalizing these local distribution functions to obtain a distribution function that pertains to the data as a whole.[3][4][5][6] If the local distribution function is a parametric distribution, such as a symmetric bivariate normal distribution then the method is referred to as a kernel method, but more correctly should be designated as a parametric kernel method. On the other hand, if the local kernel element associated with each point is a local convex polygon constructed from the point and its k-1 nearest neighbors, then the method is nonparametric and referred to as a k-LoCoH or fixed point LoCoH method. This is in contrast to r-LoCoH (fixed radius) and a-LoCoH (adaptive radius) methods.
In the case of LoCoH utilization distribution constructions, the home range can be taken as the outer boundary of the distribution (i.e. the 100th percentile). In the case of utilization distributions constructed from unbounded kernel elements, such as bivariate normal distributions, the utilization distribution is itself unbounded. In this case the most often used convention is to regard the 95th percentile of the utilization distribution as the boundary of the home range.
To construct a k-LoCoH utilization distribution:
- Locate the k − 1 nearest neighbors for each point in the dataset.
- Construct a convex hull for each set of nearest neighbors and the original data point.
- Merge these hulls together from smallest to largest.
- Divide the merged hulls into isopleths where the 10% isopleth contains 10% of the original data points, the 100% isopleth contains all the points, etc.
In this sense, LoCoH methods are a generalization of the home range estimator method based on constructing the minimum convex polygon (MCP) associated with the data. The LoCoH method has a number of advantages over parametric kernel methods. In particular:
- As more data are added, the estimates of the home range become more accurate than for bivariate normal kernel constructions.
- LoCoH handles 'sharp' features such as lakes and fences much better than parametric kernel constructions.
- As mentioned above, the home range is a finite region without having to resort to an ad-hoc choice, such as the 95th percentile to obtain bounded region.
LoCoH has a number of implementations including a LoCoH Web Application.
LoCoH was formerly known as k-NNCH, for k-nearest neighbor convex hulls. It has recently been shown that the a-LoCoH is the best of the three LoCoH methods mentioned above (see Getz et al. in the references below).
T-LoCoH
T-LoCoH (time local convex hull) is an enhanced version of LoCoH which incorporates time into the home range construction.[7][8] Time is incorporated into the algorithm via an alternative measure of 'distance', called time scaled distance (TSD), which combines the spatial distance and temporal distance between any two points. This presumes that each point has a time stamp associated with it, as with GPS data. T-LoCoH uses TSD rather than Euclidean distance to identify each point's nearest neighbors, resulting in hulls that are localized in both space and time. Hulls are then sorted and progressively unioned into isopleths. Like LoCoH, UDs created by T-LoCoH generally do a good job modeling sharp edges in habitat such as water bodies; in addition T-LoCoH isopleths can delineate temporal partitions of space use.[7] T-LoCoH also offers additional sorting options for hulls, allowing it to generate isopleths that differentiate internal space by both intensity of use (the conventional UD) and a variety of behavioral proxies, including directionality and time use metrics.
Time scaled distance
The TSD for any two locations i and j separated in time by 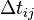 is given by
is given by

Conceptually, TSD transforms the period of time between two observations into spatial units by estimating how far the individual could have traveled during the time period if it had been moving at its maximum observed speed. This theoretical movement distance is then mapped onto a third axis of space, and distance calculated using standard Euclidean distance equations. The TSD equation also features a scaling parameter s which controls the degree to which the temporal difference scales to spatial units. When s=0, the temporal distance drops out and TSD is equivalent to Euclidean distance (thus T-LoCoH is backward compatible with LoCoH[8]). As s increases, the temporal distance becomes more and more influential, eventually swamping out the distance in space. The TSD metric is not based on a mechanistic or diffusion model of movement, but merely serves to generate hulls that are local in space and/or time.[7]
References
- ↑ Getz, W. M. and C. C. Wilmers, 2004. A local nearest-neighbor convex-hull construction of home ranges and utilization distributions. Ecography 27: 489-505.View PDF
- ↑ Getz, W.M, S. Fortmann-Roe, P. C. Cross, A. J. Lyons, S. J. Ryan, C.C. Wilmers, PLoS ONE 2(2): e207. doi:10.1371/journal.pone.0000207. LoCoH: nonparametric kernel methods for constructing home ranges and utilization distributions. View PDF
- ↑ Silverman BW. (1986) Density estimation for statistics and data analysis. London: Chapman and Hall. 176 p.
- ↑ Worton BJ. (1987). A review of models of home range for animal movement. Ecological Modelling, 38: 277–298.
- ↑ Worton BJ. (1989) Kernel methods for estimating the utilization distribution in home-range studies. Ecology 70: 164–168.
- ↑ Seaman DE, Powell RA. (1996) An evaluation of the accuracy of kernel density estimators for home range analysis. Ecology 77: 2075–2085.
- ↑ 7.0 7.1 7.2 Lyons, A., Turner, W.C., and WM Getz. 2013. Home range plus: A space-time characterization of movement over real landscapes. BMC Movement Ecology 1:2. doi:10.1186/2051-3933-1-2.
- ↑ 8.0 8.1 http://tlocoh.r-forge.r-project.org