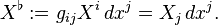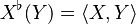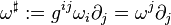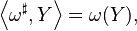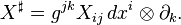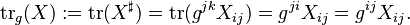Musical isomorphism

In mathematics, the musical isomorphism (or canonical isomorphism) is an isomorphism between the tangent bundle TM and the cotangent bundle T^∗M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds. The term musical refers to the use of the symbols ♭ and ♯.

It is also known as raising and lowering indices.

Discussion

Let (M, g) be a Riemannian manifold. Suppose {∂_i} is a local frame for the tangent bundle TM with dual coframe {dxⁱ}. Then, locally, we may express the Riemannian metric (which is a 2-covariant tensor field which is symmetric and positive-definite) as g = g_ij dxⁱ ⊗ dx^j (where we employ the Einstein summation convention). Given a vector field X = Xⁱ∂_i we define its flat by

$X^\flat := g_{ij} X^i \, dx^j=X_j \, dx^j.$

This is referred to as "lowering an index". Using the traditional diamond bracket notation for inner product defined by g, we obtain the somewhat more transparent relation

$X^\flat (Y) = \langle X, Y \rangle$

for all vectors X and Y.

Alternatively, given a covector field ω = ω_i dxⁱ we define its sharp by

$\omega^\sharp :=g^{ij} \omega_i \partial_j = \omega^j \partial_j$

where g^ij are the elements of the inverse matrix to g_ij. Taking the sharp of a covector field is referred to as "raising an index". In inner product notation, this reads

$\left \langle \omega^\sharp, Y \right \rangle = \omega(Y),$

for ω an arbitrary covector and Y an arbitrary vector.

Through this construction we have two inverse isomorphisms

$\flat:TM \to T^*M, \qquad \sharp:T^*M \to TM.$

These are isomorphisms of vector bundles and hence we have, for each p in M, inverse vector space isomorphisms between T_pM and T^∗
_pM.

The musical isomorphisms may also be extended to the bundles

$\bigotimes ^k TM, \qquad \bigotimes ^k T^*M.$

It must be stated which index is to be raised or lowered. For instance, consider the (2, 0) tensor field X = X_ij dxⁱ ⊗ dx^j. Raising the second index, we get the (1, 1) tensor field

$X^\sharp = g^{jk}X_{ij} \, dx^i \otimes \partial _k.$

Trace of a tensor through a metric

Given a (0, 2) tensor field X = X_ij dxⁱ ⊗ dx^j, we define the trace of X through the metric g by

$\operatorname{tr}_g(X):=\operatorname{tr}(X^\sharp)=\operatorname{tr}(g^{jk}X_{ij}) = g^{ji}X_{ij} = g^{ij}X_{ij}.$

Observe that the definition of trace is independent of the choice of index we raise since the metric tensor is symmetric.

See also

• Duality (mathematics)
• Raising and lowering indices
• Bilinear products and dual spaces
• Vector bundle
• Flat (music) and Sharp (music) about the signs ♭ and ♯