Ponytail

This article is about the hairstyle. For the band, see Ponytail (band).

A woman's ponytail from the side

A woman's ponytail from the back

To make a ponytail, some, most or all of the hair on the head is pulled away from the face, gathered and secured at the back of the head with a hair tie, clip, or other similar device and allowed to hang freely from that point. It gets its name from its resemblance to the undocked tail of a horse or pony. Ponytails are most commonly gathered at the middle of the back of the head, or the base of the neck. Depending on fashions, they may also be worn at the side of the head (which is sometimes considered formal) which is worn over one ear, or on the very top of the head (allowing the hair to fall down the back or one side of the head).

If the hair is divided so that it hangs in two sections they are called "ponytails" or bunches, if left loose, and pigtails, plaits or braids if plaited. Unbraided ponytails worn above each ear are sometimes called dog-ears.

It is common for those who wear tight ponytails to experience traction alopecia, a form of hair loss. Sometimes it can cause a headache.

Ponytails on women and girls

Detail from an 18th-century engraving showing a girl (left) with a ponytail

Women (as opposed to girls) complying with European fashion of the Georgian period and to the 20th century rarely were seen outside of the boudoir with their hair in such an informal style as a ponytail.

Today, women commonly wear their hair in ponytails in informal and office settings or when exercising; they are likely to choose more-elaborate styles (such as braids and those involving accessories) for formal occasions. It is a practical choice as it keeps hair out of the eyes. It will keep the hair off the neck as well. The ponytail is also popular with school-aged girls, partly because flowing hair is often associated with youth and because of its simplicity; a young girl is likely to be able to retie her own hair after a sports class, for example. A ponytail can also be a fashion statement; sometimes meaning sporty, other times a low pony tail sends signals of a chic personality.

As a man's hairstyle

Man's white-haired ponytail on a black background.

In the late 18th century, men often tied their ponytails with a black ribbon.

In the late 1980s, a short ponytail was seen as an impudent, edgy look for men who wanted to individualize, but keep their hair flat and functional (see mullet). Steven Seagal's ponytail in Marked for Death is an example of such.

Men who wear their hair long, or sometimes in mullets, frequently tie it back into a ponytail, but avoid the top- or side-of-the-head variants, although these variants can be used for practical reasons for keeping it off the neck.

In the second half of the 18th century, most men in Europe wore their hair long and tied back into what we would now describe as a ponytail, although it was sometimes gathered into a silk bag rather than allowed to hang freely. At that time, it was commonly known by the French word for "tail", queue. It was a mandatory hairstyle for men in all European armies until the early 19th century, after most civilians had stopped wearing queues. The British Army was the first to dispense with it, and by the end of the Napoleonic Wars most armies had changed their regulations to make short hair compulsory.

"Queue" was also the word used to refer to the waist-length pigtail which the ruling Manchus made Han Chinese men wear during the Qing Dynasty in China.

Scientific studies

File:Lindageorge.jpg

A dark-haired woman with a ponytail.

The first equation of state for hair was developed by C F van Wyk in 1946.

Scientists in the UK have formulated a mathematical model that predicts the shape of a ponytail given the length and random curvature (or curliness) of a sample of individual hairs. The Ponytail Shape Equation provides an understanding of how a ponytail is swelled by the outward pressure which arises from interactions between the component hairs.

The researchers developed a general continuum theory for a bundle of hairs, treating each hair as an elastic filament with random intrinsic curvature. From this they created a differential equation for the shape of the bundle relating the elasticity, gravity, and orientational disorder and extracted a simple equation of state to relate the swelling pressure to the measured random curvatures of individual hairs. The equation itself is a fourth order non linear differential equation.

The Rapunzel number is a ratio used in this equation to calculate the effects of gravity on hair relative to its length. This number determines whether a ponytail looks like a fan or whether it arcs over and becomes nearly vertical at the bottom. A short ponytail of springy hair with a low Rapunzel number, fans outward. A long ponytail with a high Rapunzel number, hangs down, as the pull of gravity overwhelms the springiness.

It is now also known why jogger's ponytails swing side to side. An up and down motion is too unstable: a ponytail cannot sway forward and backward because the jogger’s head is in the way. Any slight jostling causes the up and down movement to become a side to side sway.

The research on the shape of the ponytail won the authors the Ig Nobel for Physics in 2012.

Ponytail equation

The ponytail equation is

$l^3 R_{ssss} - ( L - s ) R_{ss} + R_s - \pi ( R ) = 0$

where

$\pi( R ) = \frac{ 4 l^3 P }{ A \rho R }$

In these equations l is the length at which gravity bends the hair

$l = ( \frac{ A }{ \lambda g } )^\frac{ 1 }{ 3 }$

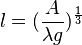
where g is the acceleration due to gravity, A is the bending modulus and λ is the density of the hair. A is defined to be

$A = \frac{ E \pi d^4 }{ 64 }$

E is a constant equal to 4 gigaPascal and d is the average diameter of the hair.

L is the length of the switch of hair in the ponytail, R is the ponytail radius, s is the arc length from the clamp on the ponytail, P is the pressure due to the clamp and ρ is the hair density

$\rho = \frac{ N }{ \pi R^2 }$

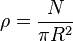
where N is the number of hairs in the ponytail. R_s is the partial derivative of R with respect to s.

The Rapunzel number (Ra) is the ratio

$Ra = \frac{ L }{ l }$

The numerical values used in this equation were the average density of human hair (1.3 grams per cubic centimeter), a bending modulus ( A ) of 8 x 10⁻⁹ Newton meter², a linear mass density of hair ( λ ) of 65 microgrammes per centimeter and the major diameter of the hair (human hair is elliptical in cross section) of 79 +/- 16 micrometers. N was taken to be 100,000 - the average numbers of hairs on a human head. The constant E was that of nylon which is similar to hair in its bend and twist moduli. The length L was taken to be 25 centimeters. These values give a length at which gravity bends a hair of l = 5.

The authors found empirically that by ignoring the second and fourth order derivatives of R with respect to s in the equation allowed for an exact solution to the equation that produced an excellent fit to the observed ponytails.

The authors also found that the spread of the ponytail around the anteroposterior axis (front-back) was symmetrical and made an angle of ~17 degrees with this axis. This angle was approximately constant in all the lengths tested.

See also

• List of hairstyles
• Sailendra Nath Roy