ProbCons

ProbCons is an open source probabilistic consistency-based multiple alignment of amino acid sequences. It is an efficient protein multiple sequence alignment program, which has demonstrated a statistically significant improvement in accuracy compared to several leading alignment tools.

Algorithm

The following describes the basic outline of the ProbCons algorithm.

Step 1: Reliability of an alignment edge

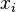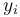For every pair of sequences compute the probability that letters $x_i$ and $y_i$ are paired in 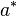$a^*$ an alignment that is generated by the model.

$\begin{align} P(x_i \sim y_i|x,y) & \stackrel{def}{=} Pr[x_i \sim y_i \text{ in some a }|x,y] \\ & = \sum_{\text{alignment a with }x_i - y_i} Pr[a|x,y]\\ & = \sum_{\text{alignment a}} \mathbf{1}\{x_i - y_i \in a\} Pr[a|x,y] \end{align}$

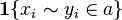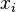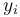(Where $\mathbf{1}\{x_i \sim y_i \in a\}$ is equal to 1 if $x_i$ and $y_i$ are in the alignment and 0 otherwise.)

Step 2: Maximum expected accuracy

The accuracy of an alignment 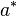$a^*$ with respect to another alignment 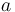$a$ is defined as the number of common aligned pairs divided by the length of the shorter sequence.

Calculate expected accuracy of each sequence:

$\begin{align} E_{Pr[a|x,y]}(acc(a^*,a)) & = \sum_{a}Pr[a|x,y]acc(a^*,a) \\ & = \frac{1}{min(|x|,|y|)} \cdot \sum_{a}\mathbf{1}\{x_i \sim y_i \in a\} Pr[a|x,y]\\ & = \frac{1}{min(|x|,|y|)} \cdot \sum_{x_i - y_i} P(x_i \sim y_j|x,y) \end{align}$

This yields a maximum expected accuracy (MEA) alignment:

$E(x,y) = \arg\max_{a^*} \; E_{Pr[a|x,y]}(acc(a^*,a))$

Step 3: Probabilistic Consistency Transformation

All pairs of sequences x,y from the set of all sequences 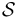$\mathcal{S}$ are now re-estimated using all intermediate sequences z:

$P'(x_i - y_i|x,y) = \frac{1}{|\mathcal{S}|} \sum_{z} \sum_{1 \leq k \leq |z|} P(x_i \sim z_i|x,z) \cdot P(z_i \sim y_i|z,y)$

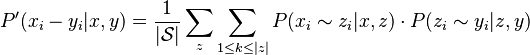
This step can be iterated.

Step 4: Computation of guide tree

Construct a guide tree by hierarchical clustering using MEA score as sequence similarity score. Cluster similarity is defined using weighted average over pairwise sequence similarity.

Step 5: Compute MSA

Finally compute the MSA using progressive alignment or iterative alignment.

See also

• Sequence alignment software
• Clustal
• MUSCLE
• AMAP
• T-Coffee
• Probalign
• ProbConsRNA — for nucleotide sequences

External links

• Official website