Snub polyhedron

Polyhedron
Class	Number and properties
Platonic solids	(5, convex, regular)
Archimedean solids	(13, convex, uniform)
Kepler–Poinsot polyhedra	(4, regular, non-convex)
Uniform polyhedra	(75, uniform)
Prismatoid: prisms, antiprisms etc.	(4 infinite uniform classes)
Polyhedra tilings	(11 regular, in the plane)
Quasi-regular polyhedra	(8)
Johnson solids	(92, convex, non-uniform)
Pyramids and Bipyramids	(infinite)
Stellations	Stellations
Polyhedral compounds	(5 regular)
Deltahedra	(Deltahedra, equalatial triangle faces)
Snub polyhedra	(12 uniform, not mirror image)
Zonohedron	(Zonohedra, faces have 180°symmetry)
Dual polyhedron
Self-dual polyhedron	(infinite)
Catalan solid	(13, Archimedean dual)

A snub polyhedron is a polyhedron obtained by alternating a corresponding omnitruncated polyhedron.

Chiral snub polyhedra do not have reflection symmetry and hence have two enantiomorphous forms which are reflections of each other. Their symmetry groups are all point groups and are one of:

• O - chiral octahedral symmetry; the rotation group of the cube and octahedron; order 24.
• I - chiral icosahedral symmetry; the rotation group of the icosahedron and the dodecahedron; order 60.

For example, the snub cube:

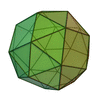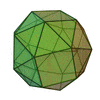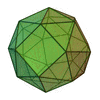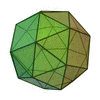Snub polyhedra have Wythoff symbol | p q r and by extension, vertex configuration 3.p.3.q.3.r. Retrosnub polyhedra (a subset of the snub polyhedron, containing the great icosahedron, small retrosnub icosicosidodecahedron, and great retrosnub icosidodecahedron) still have this form of Wythoff symbol, but their vertex configurations are instead ^{(3.−p.3.−q.3.−r)}/₂.

Among the snub polyhedra that cannot be otherwise generated, only the pentagonal antiprism, pentagrammic antiprism, pentagrammic crossed-antiprism, small snub icosicosidodecahedron and small retrosnub icosicosidodecahedron are known to occur in any non-prismatic uniform 4-polytope. The tetrahedron, octahedron, icosahedron, and great icosahedron appear commonly in non-prismatic uniform 4-polytopes, but not in their snub constructions. Every snub polyhedron however can appear in the polyhedral prism based on them.

List of snub polyhedra

Uniform

There are 12 uniform snub polyhedra, not including the icosahedron as a snub tetrahedron, the great icosahedron as a retrosnub tetrahedron and the great disnub dirhombidodecahedron, also known as Skilling's figure.

When the Schwarz triangle of the snub polyhedron is isosceles, the snub polyhedron is not chiral. This is the case for the icosahedron, great icosahedron, small snub icosicosidodecahedron, and small retrosnub icosicosidodecahedron.

In the pictures of the snub derivation (showing a distorted snub polyhedron, topologically identical to the uniform version, arrived at from geometrically alternating the parent uniform omnitruncated polyhedron) where green is not present, the faces derived from alternation are coloured red and yellow, while the snub triangles are blue. Where green is present (only for the snub icosidodecadodecahedron and great snub dodecicosidodecahedron), the faces derived from alternation are red, yellow, and blue, while the snub triangles are green.

Snub polyhedron	Image	Original omnitruncated polyhedron	Image	Snub derivation	Symmetry group	Wythoff symbol Vertex description
Icosahedron (snub tetrahedron)		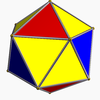Truncated octahedron	100px	100px	Ih (Th)	| 3 3 2 3.3.3.3.3
Great icosahedron (retrosnub tetrahedron)		Truncated octahedron	100px	100px	Ih (Th)	| 2 3/2 3/2 (3.3.3.3.3)/2
Snub cube		Truncated cuboctahedron		100px	O	| 4 3 2 3.3.3.3.4
Snub dodecahedron		Truncated icosidodecahedron		100px	I	| 5 3 2 3.3.3.3.5
Small snub icosicosidodecahedron		Doubly covered truncated icosahedron		100px	Ih	| 3 3 5/2 3.3.3.3.3.5/2
Snub dodecadodecahedron		Small rhombidodecahedron with extra 12{10/2} faces		100px	I	| 5 5/2 2 3.3.5/2.3.5
Snub icosidodecadodecahedron		Icositruncated dodecadodecahedron		100px	I	| 5 3 5/3 3.5/3.3.3.3.5
Great snub icosidodecahedron		Rhombicosahedron with extra 12{10/2} faces		100px	I	| 3 5/2 2 3.3.5/2.3.3
Inverted snub dodecadodecahedron		Truncated dodecadodecahedron		100px	I	| 5 2 5/3 3.5/3.3.3.3.5
Great snub dodecicosidodecahedron		Great dodecicosahedron with extra 12{10/2} faces		no image yet	I	| 3 5/2 5/3 3.5/3.3.5/2.3.3
Great inverted snub icosidodecahedron		Great truncated icosidodecahedron		100px	I	| 3 2 5/3 3.5/3.3.3.3
Small retrosnub icosicosidodecahedron		Doubly covered truncated icosahedron		no image yet	Ih	| 5/2 3/2 3/2 (3.3.3.3.3.5/2)/2
Great retrosnub icosidodecahedron		Great rhombidodecahedron with extra 20{6/2} faces		no image yet	I	| 2 5/3 3/2 (3.3.3.5/2.3)/2
Great dirhombicosidodecahedron		—	—	—	Ih	| 3/2 5/3 3 5/2 (4.3/2.4.5/3.4.3.4.5/2)/2
Great disnub dirhombidodecahedron		—	—	—	Ih	| (3/2) 5/3 (3) 5/2 (3/2.3/2.3/2.4.5/3.4.3.3.3.4.5/2.4)/2

Notes:

• The icosahedron, snub cube and snub dodecahedron are the only three convex ones. They are obtained by snubification of the truncated octahedron, truncated cuboctahedron and the truncated icosidodecahedron - the three convex truncated quasiregular polyhedra.
• The only snub polyhedron with the chiral octahedral group of symmetries is the snub cube.
• Only the icosahedron and the great icosahedron are also regular polyhedra. They are also deltahedra.
• Only the icosahedron, great icosahedron, small snub icosicosidodecahedron, small retrosnub icosicosidodecahedron, great dirhombicosidodecahedron, and great disnub dirhombidodecahedron also have reflective symmetries.

There is also the infinite set of antiprisms. They are formed from prisms, which are truncated hosohedra, degenerate regular polyhedra. Those up to hexagonal are listed below. In the pictures showing the snub derivation, the faces derived from alternation (of the prism bases) are coloured red, and the snub triangles are coloured yellow.

Snub polyhedron	Image	Original omnitruncated polyhedron	Image	Snub derivation	Symmetry group	Wythoff symbol Vertex description
Tetrahedron		Cube		100px	Td (D2d)	| 2 2 2 3.3.3
Octahedron		Hexagonal prism	100px	100px	Oh (D3d)	| 3 2 2 3.3.3.3
Square antiprism		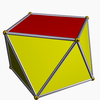Octagonal prism		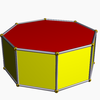100px	D4d	| 4 2 2 3.4.3.3
Pentagonal antiprism		Decagonal prism		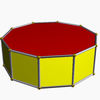100px	D5d	| 5 2 2 3.5.3.3
Pentagrammic antiprism		Doubly covered pentagonal prism		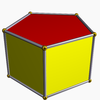100px	D5h	| 5/2 2 2 3.5/2.3.3
Pentagrammic crossed-antiprism		Decagrammic prism		100px	D5d	| 2 2 5/3 3.5/3.3.3
Hexagonal antiprism		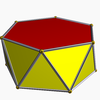Dodecagonal prism		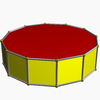100px	D6d	| 6 2 2 3.6.3.3

Notes:

• Two of these polyhedra may be constructed from the first two snub polyhedra in the list starting with the icosahedron: the pentagonal antiprism is a parabidiminished icosahedron and a pentagrammic crossed-antiprism is a parabidiminished great icosahedron, also known as a parabireplenished great icosahedron.

Non-uniform

Two Johnson solids are snub polyhedra: the snub disphenoid and the snub square antiprism. Neither is chiral.

Snub polyhedron	Image	Original polyhedron	Image	Symmetry group
Snub disphenoid		Disphenoid		D2d
Snub square antiprism		Square antiprism		D4d

References

• Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993.

Polyhedron operators

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}